材料が降伏(破壊)するか否かを判定する基準を「降伏条件」と言います。
材料力学を習った方は「ミーゼスの降伏条件」や「トレスカの降伏条件」という
単語は聞き覚えがあるかと思います。
本記事では降伏条件の考え方、グラフの意味、使い分けについて詳しく解説します。
降伏条件とは
前提知識:主応力、主せん断応力について
降伏条件について解説する前に、
前提知識として「主応力」と「主せん断応力」について説明します。
主応力
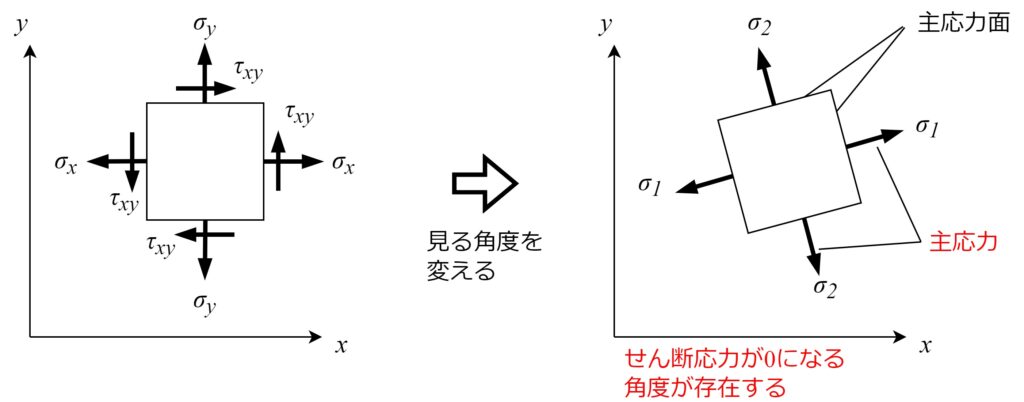
材料に加わる力は、仮想断面をどの角度で見るかによって、
垂直応力とせん断応力の組み合わせが無数に変わります。
無数の組み合わせの中で、垂直応力のみが生じ、
せん断応力が0になる仮想断面が必ず存在します。
この面を「主応力面」と呼び、
この面に垂直な応力を「主応力」と呼びます。
(詳しくは日本機械学会サイトを参照)
2次元応力状態の場合は垂直に2軸、3次元応力状態の場合は3軸の
主応力が存在します
主せん断応力
上記と同様に、垂直応力とせん断応力の無数の組み合わせの中で、
せん断応力が極値となる仮想断面も必ず存在します。
(ただし垂直応力は0ではない)
この面を「主せん断応力面」と呼び、
この面にかかるせん断応力を「主せん断応力」と呼びます。
(詳しくは日本機械学会サイトを参照)
主せん断応力の大きさは(最大主応力―最小主応力)÷2に等しく、
主せん断応力面は主応力面を45°傾けた位置にあります。
降伏条件とは何か
単純引張・圧縮の1軸の応力を受ける部材では、
軸方向応力が降伏応力に達すると降伏し、塑性変形が始まると考えます。
しかし実際の機械や構造物では、3次元的に多方向に応力が加わることが多く、
複雑な応力状態を考慮する必要があります。
多方向に応力が加わるときに、どういった条件・組み合わせで部材が降伏するか、
を判断するための基準を「降伏条件」と呼びます。
過去の学者達が実験を繰り返して降伏条件を定式化しようと試み、
これまでいくつかの「説」が提案されています。
本記事では代表的な3つの説(=降伏条件)について解説します。
なお、本記事の解説は下記の書籍を参考にしています。
図解が多く、材料力学を勉強するには最適な教科書だと思います。
私も購入して10年経ちますが、いまだに仕事や資格勉強で使うのでオススメです。
説1:最大主応力説
降伏条件の考え方
材料内の3つの主応力\(\sigma_1,\sigma_2,\sigma_3\)のうち、
最大の主応力が降伏応力\(\sigma_Y\)に到達すると降伏するというシンプルな考え方です。
この説に基づく降伏条件を式で書くと、次のようになります。
$$\rm{max}(\left|\sigma_1\right|,\left|\sigma_2\right|,\left|\sigma_3\right|)=\sigma_Y$$
応力状態のグラフ
最大主応力説をグラフにすると以下のようになります。
簡単のため平面応力状態(\(\sigma_3=0\))としています。
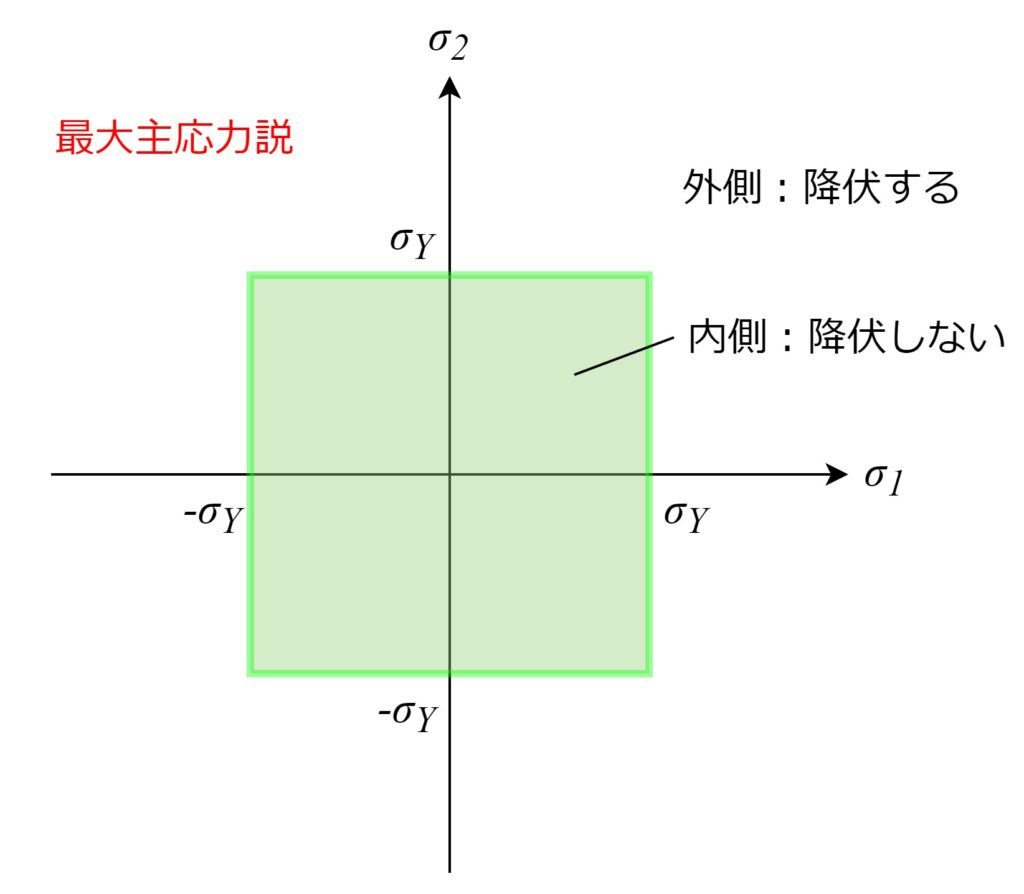
降伏条件の式と見比べると、
グラフの内側であれば材料は降伏しない、と見ることができます。
説2:トレスカの降伏条件(=最大せん断応力説)
降伏条件の考え方
材料内の3つの主せん断応力\(\tau_1,\tau_2,\tau_3\)のうち、
主せん断応力の最大値が限界値(降伏応力\(\sigma_Y\)の半分)に到達すると降伏する
という考え方です。
この説に基づく降伏条件を式で書くと、次のようになります。
$$\rm{max}(\tau_1,\tau_2,\tau_3)=(\sigma_{max}-\sigma_{min})/2=\sigma_Y/2$$
ただし\(\sigma_{max}\)は最大主応力、\(\sigma_{min}\)は最小主応力です。
応力状態のグラフ
トレスカの降伏条件をグラフにすると以下のようになります。
簡単のため平面応力状態(\(\sigma_3=0\))としています。
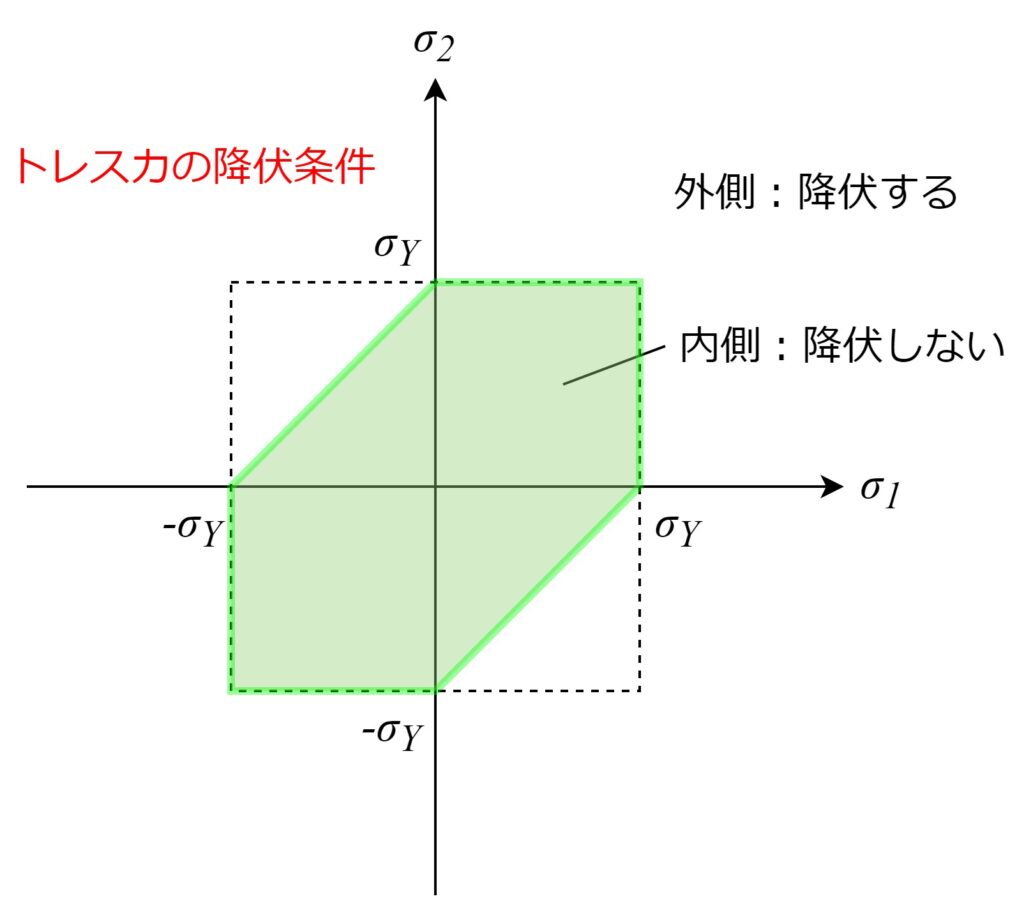
こちらも降伏条件の式と見比べると、
グラフの内側であれば材料は降伏しない、と見ることができます。
グラフの意味を考察
最大主応力説のグラフと比較すると、
\(\sigma_1\)が正かつ\(\sigma_2\)が負の領域と、\(\sigma_1\)が負かつ\(\sigma_2\)が正の領域
(=\(\sigma_1\)と\(\sigma_2\)の符号が異なる領域)が狭くなっていることが分かります。
この意味を考えるため、
下の図のように縦に\(\sigma_1\)で引っ張られる部材を考えます。
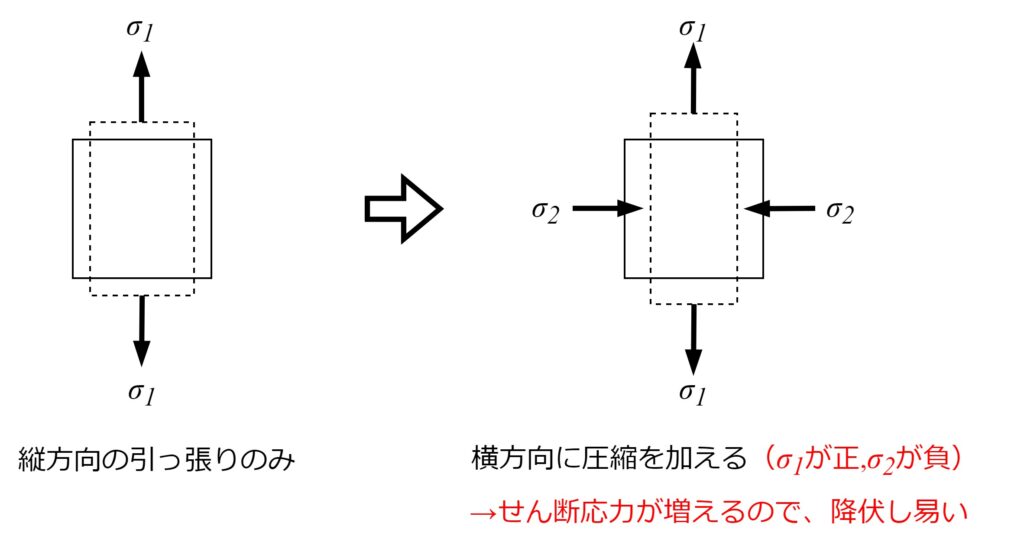
縦に\(\sigma_1\)で引っ張られながら、さらに横から\(\sigma_2\)で圧縮されると、
内部ではせん断応力が増えます。
この条件が、\(\sigma_1\)で引っ張られていただけの時より、
壊れやすいと考えるため、トレスカの降伏条件のグラフは
\(\sigma_1\)と\(\sigma_2\)の符号が異なる領域が削られた形をしています。
説3:ミーゼスの降伏条件(=最大せん断ひずみエネルギー説)
降伏条件の考え方
材料内の最大せん断ひずみエネルギーの値が、
限界値に達すると降伏するという考え方です。
全ひずみエネルギーから、体積変化によるひずみエネルギーを差し引くと、
せん断ひずみエネルギーが求められます。
これが破壊を決定付けると考えます。
この説に基づく降伏条件を式で書くと、次のようになります。
$$\sqrt{\frac{(\sigma_1-\sigma_2)^2+(\sigma_2-\sigma_3)^2+(\sigma_3-\sigma_1)^2}{2}}=\sigma_{Mises}=\sigma_Y$$
\(\sigma_{Mises}\)はミーゼス応力(あるいは相当応力)と呼ばれます。
なお設計の実務においては、せん断応力の許容値=降伏応力\(\times 1/\sqrt{3}\)倍として計算しますが、これはミーゼスの降伏条件によるものです。詳しくは別の記事で解説しています。
物体内の二つの平面が互いにずれるような変形を「せん断」と言い、この時にかかる力を「せん断力」と言います。機械設計においては曲げや引張と合わせて、せん断についての考慮も欠かせません。 本記事では、せん断力の意味・求め方・許容値など[…]
応力状態のグラフ
ミーゼスの降伏条件をグラフにすると以下のような楕円形なります。
簡単のため平面応力状態(\(\sigma_3=0\))としています。
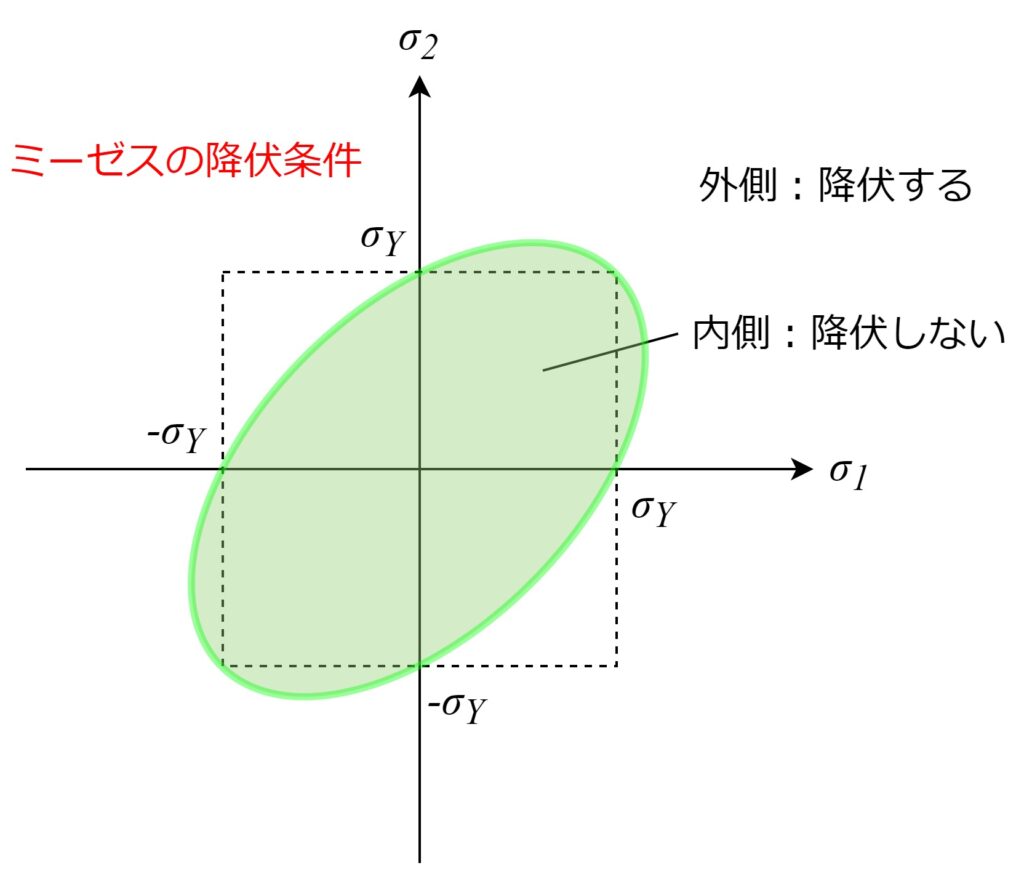
グラフの内側であれば材料は降伏しない、と見ることができます。
グラフの意味を考察
シンプルな最大主応力説のグラフと見比べると、
最大主応力説より外側(=ミーゼスの降伏条件の方が壊れにくい)の領域と、
最大主応力説より内側(=ミーゼスの降伏条件の方が壊れやすい)の領域があります。
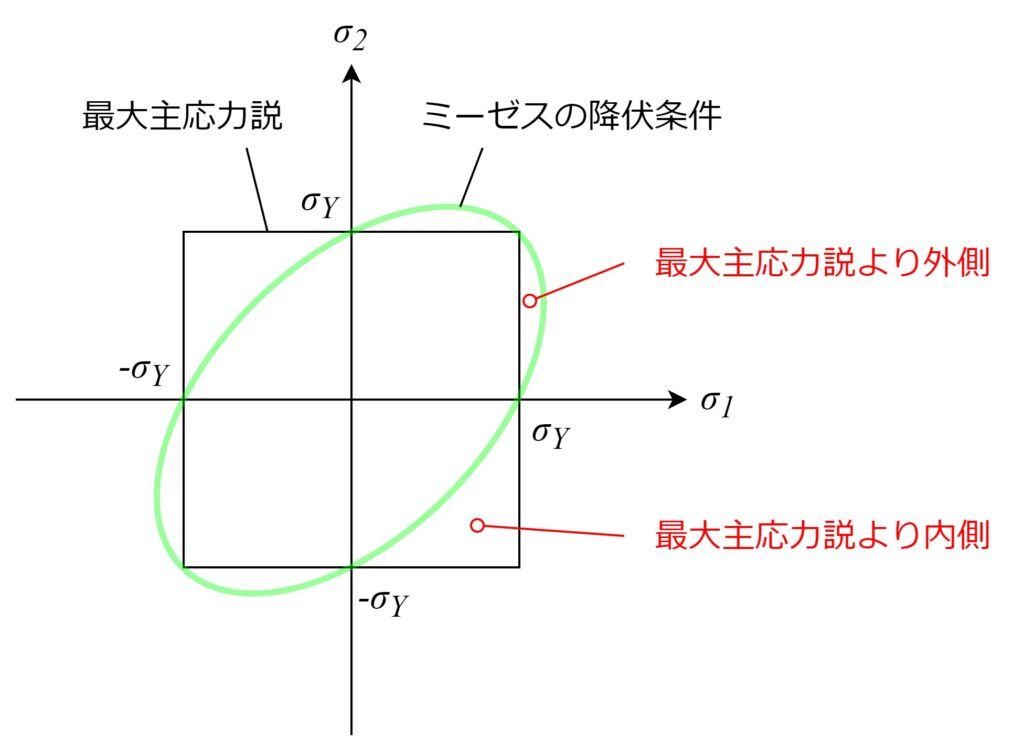
このイメージを掴むために下の図のような平面応力状態を考えます。
部材が縦方向に\(\sigma_1\)で引っ張られると、
部材は縦方向には伸びて、横方向には縮みます。
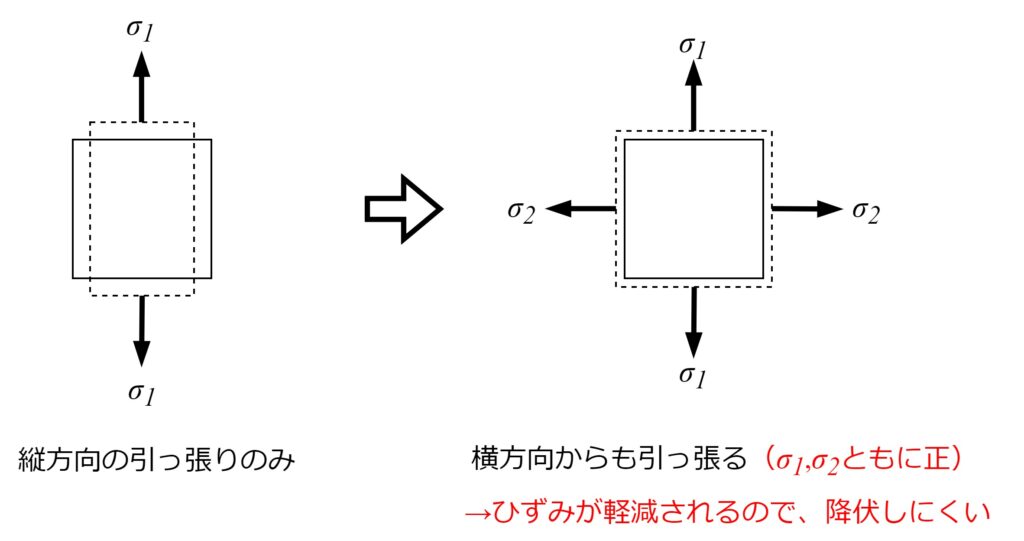
この状態で横方向にも\(\sigma_2\)で引っ張ると、ひずみを減らす方向に
力が加わることになります。
ミーゼスの降伏条件はひずみエネルギーの大小で降伏を判断するので、
ひずみが減る方向となる「\(\sigma_1\)と\(\sigma_2\)の符号が同じ領域」では、
最大主応力説よりも降伏しにくい条件となっています。
反対に、ひずみが増える方向となる「\(\sigma_1\)と\(\sigma_2\)の符号が異なる領域」では、
最大主応力説よりも降伏しやすい条件となっています。
3つの降伏条件(説)の使い分け
ミーゼスの降伏条件とトレスカの降伏条件の数値差
ミーゼスの降伏条件とトレスカの降伏条件のグラフを重ねると
以下のようになります。
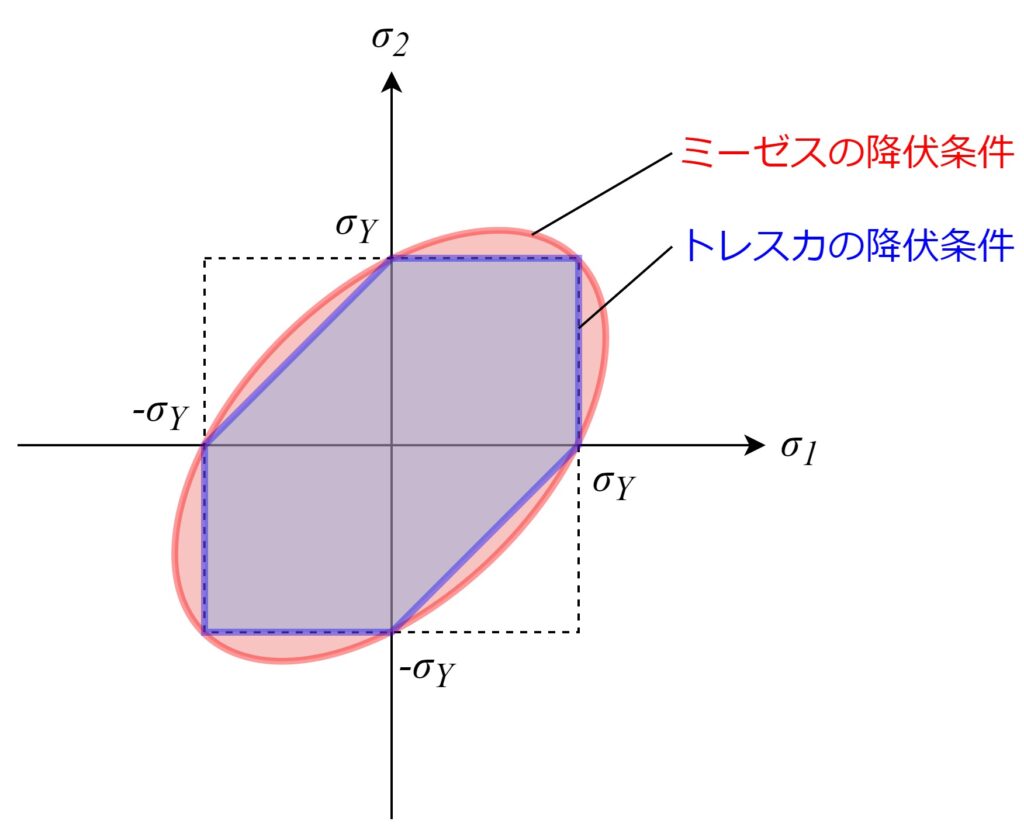
内側にあるトレスカの降伏条件の方が、
より厳しい降伏条件であることが分かります。
各々の降伏条件の式より計算すると、
ミーゼスの降伏条件とトレスカの降伏条件の数値的な差は、
最大で約15%(\(2/\sqrt{3}\)倍)となります。
どの降伏条件を使えばよいのか?
降伏条件の説を3つ紹介しましたが、
「この説が正しい」という絶対的な正解があるわけではなく、
どの条件を使うかは設計者次第となります。
ただし経験的に、どの材料がどの降伏条件に近いかが分かってきており、
一般的に以下のように使い分けられます。
| 降伏条件(説) | 材料 | 備考 |
|---|---|---|
| 最大主応力説 | 鋳鉄のような脆性材料 (FC,FCDなど) | 延性材料には 当てはまらないことが多い |
| トレスカの降伏条件 (=最大せん断応力説) | 延性材料 (SS,SUS,S〇〇C,銅合金など) | ミーゼスの降伏条件よりも 厳しめの条件で考えたいときに 使われる |
| ミーゼスの降伏条件 (=最大せん断ひずみエネルギー説) | 延性材料 (SS,SUS,S〇〇C,銅合金など) | 延性材料では近年の主流。 シミュレーション計算などで よく用いられる |
延性材料ではミーゼスの降伏条件とトレスカの降伏条件のどちらも
実験結果とよく一致します。
ただし近年は、シミュレーション計算に向いている
ミーゼスの降伏条件が使われることが多くなっているようです。
ミーゼス応力はベクトルの方向によらないスカラー量として算出されるので、
シミュレーションと相性が良いためです。
まとめ
材料が降伏(破壊)するか否かを判定する基準である
「降伏条件」について解説しました。
ポイントをまとめます。
- 降伏条件には「最大主応力説」「トレスカの降伏条件」「ミーゼスの降伏条件」
がある - 脆性材料は「最大主応力説」を使う
- 延性材料は「トレスカの降伏条件」か「ミーゼスの降伏条件」を使うが、近年は「ミーゼスの降伏条件」が主流
皆様の参考になれば幸いです。






