ボールを空中に投げた時、位置エネルギーと運動エネルギーの総和は一定となり
「エネルギー保存の法則」が成り立ちます。
これを流体に当てはめたのが「ベルヌーイの定理」です。
本記事ではベルヌーイの定理・考え方を初心者にもわかりやすく解説します。
ベルヌーイの定理とは?
ベルヌーイの定理とは冒頭にも述べた通り、
「流体のエネルギー保存の法則」を示す定理です。
高校物理で習うエネルギー保存の法則では、
「運動エネルギー」と「位置エネルギー」の2つの和が一定という内容でした。
流体の場合はこれに「圧力エネルギー」が加わり、以下のようになります。

ベルヌーイの定理とは、
運動エネルギー、圧力エネルギー、位置エネルギーの3つは各々交換する事が可能で、
その総和は一定になる、という定理です。
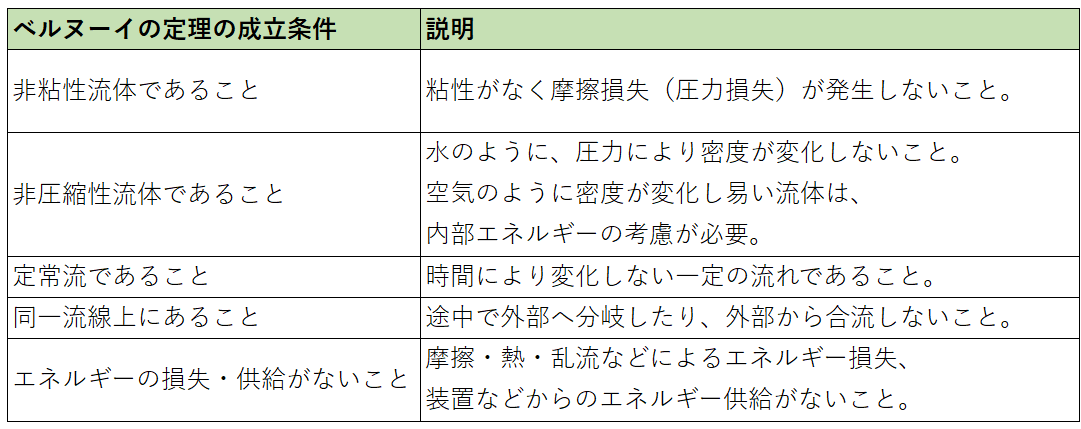
ただしこの関係は常に成り立つわけではなく、
二点が同一流線上にある場合、非粘性・非圧縮性の流体である場合
というように成り立つための条件があります。
ベルヌーイの定理が成り立つ条件については後述します。
ベルヌーイの定理の式
ベルヌーイの定理の式
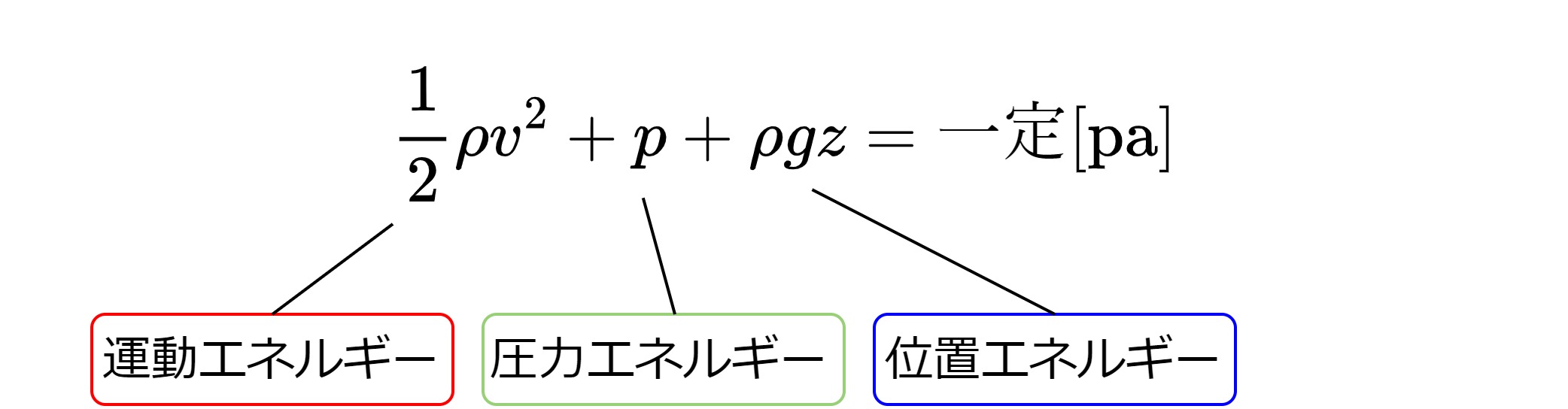
ベルヌーイの定理を式にすると次のようになります。
(これをベルヌーイの式と呼びます)
- \(\rho\):流体の密度 \(\rm{(kg/m^3)}\)
- \(v\):流速 \(\rm{(m/s)}\)
- \(p\):圧力 \(\rm{(pa)}\)
- \(g\):重力加速度 \(\rm{(m/s^2)}\)
- \(z\):高さ・水深 \(\rm{(m)}\)
左辺の3つの項は左から順に、流体の単位体積あたりの
運動エネルギー、圧力エネルギー、位置エネルギーを表します。
なぜこのような形となるかについては後述します。
上式は圧力の単位で表現されていますが、
水頭(ヘッド)での表現もよく使われます。
上式の全体を\(\rho g\)で割ると水頭\(\rm{[m]}\)の単位となり、次のようになります。
$$\frac{v^2}{2g}+\frac{p}{\rho}+z=一定\rm{[m]}$$
※水頭:水の持つエネルギーを水柱の高さに置き換えたもの
ベルヌーイの定理のイメージ
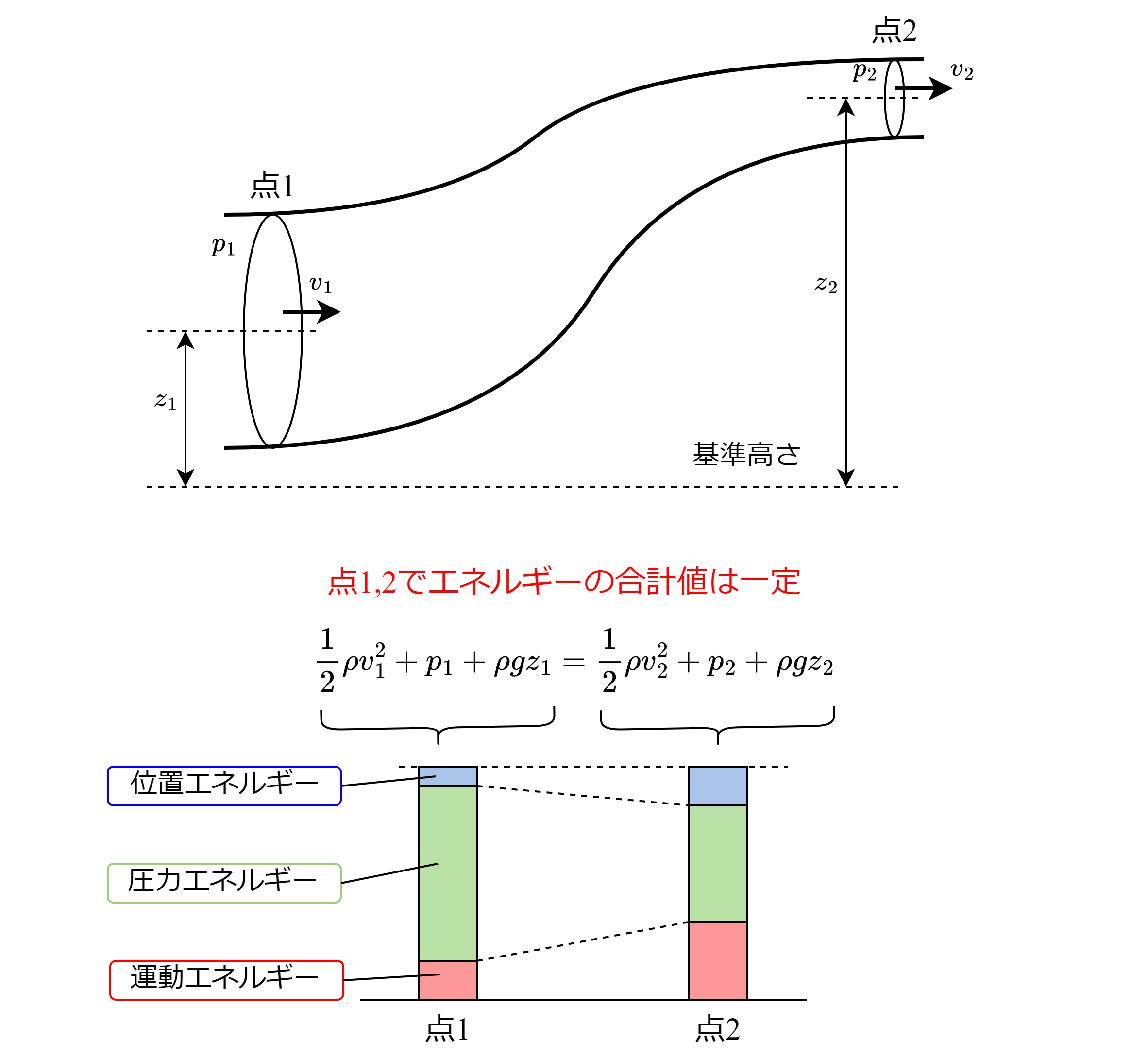
ベルヌーイの定理をイメージするため、
下の図のような流路において、点1,2の持つエネルギーを考えます。
運動エネルギー、圧力エネルギー、位置エネルギーの配分は異なっても、
合計値は点1,2で一定、というのがベルヌーイの定理です。
各エネルギーの表現について
流体の持つ各エネルギーの表現方法について解説します。
運動エネルギー
質量\(m\)の物体が速度\(v\)で動く時の運動エネルギーは\(1/2mv^2\)です。
ここで質量は密度×体積なので、\(1/2mv^2\)を体積で割ると単位体積あたりの
運動エネルギーとなり、次のように書けます。
$$ 運動エネルギー(単位体積あたり)= \frac{1}{2} \rho v^2$$
ベルヌーイの定理で出てくる項と同じ形となりました。
圧力エネルギー
圧力\(p\)がエネルギーになる、という事をイメージし易くするため、
以下のようなシリンダーを例に考えます。
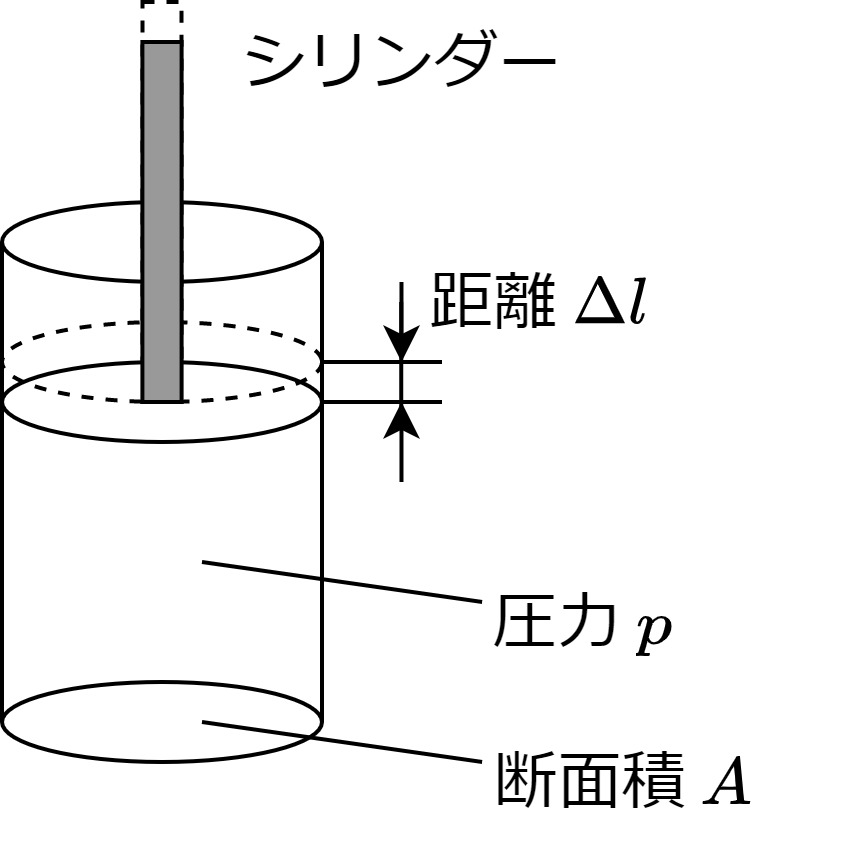
圧力\(p\)、断面積\(A\)のシリンダーが\(\Delta l\)だけ動いた時、
このシリンダーが外界にした仕事は次のようになります。
$$シリンダーがした仕事=pA\Delta l$$
これを元々シリンダーの持っていた圧力エネルギーだと考えます。
シリンダーが動く体積\(A\Delta l\)の合計で\(pA\Delta l\)のエネルギーを持っている事になるので、
単位体積あたりの圧力エネルギーは\(p\)と考える事ができます。
$$圧力エネルギー(単位体積あたり)=p$$
位置エネルギー
質量\(m\)の物体が高さ\(z\)の位置にあるとき、位置エネルギーは\(mgz\)です。
先ほどと同様、質量は密度×体積である事から、\(mgz\)を体積で割ると
単位体積あたりの位置エネルギーとなり、次のように書けます。
$$位置エネルギー(単位体積あたり)=\rho g z$$
以上により、ベルヌーイの定理の3つの項が、
それぞれ単位体積あたりの運動エネルギー、圧力エネルギー、位置エネルギーの
の形となっている事が確認できました。
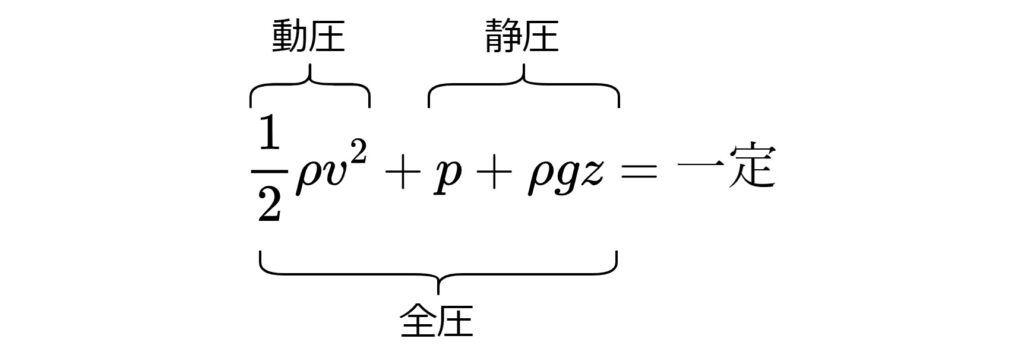
「静圧」「動圧」「全圧」とは?
ベルヌーイの定理を考える際に登場する「静圧」「動圧」「全圧」について説明します。
静圧
静圧とはベルヌーイの定理の\(p+\rho g z\)に相当し、
流体が実際に外界に及ぼす圧力を言います。
配管に設置した圧力計は、この静圧しか計測できません。
動圧
動圧とはベルヌーイの定理の\(1/2\rho v^2\)に相当し、
流体が持つ運動エネルギーを言います。
次元は圧力と一致しますが周囲の流体や外界を押す効果はありません。
仮に流体を静止できればその瞬間に発生する圧力ですが、
実際には測定することはできず、密度と流速から算出されます。
全圧
「静圧」と「動圧」の和を「全圧」といいます。
以上をまとめると、次のようになります。
ベルヌーイの定理が成立する条件
ベルヌーイの定理はとても便利な式ですが常に成り立つわけではなく、
以下の条件を満たす必要があります。
よくベルヌーイの定理の説明として、
「流速が速いところでは圧力が低い」と言われますが、
上記のように条件が限定されている事を忘れないようにしましょう。
配管の圧力損失との関係
配管を流れる流体はその粘性により配管壁面からの摩擦抵抗を受け、
エネルギーを損失します。
これを圧力損失と呼び、ベルヌーイの定理を考える際には考慮が必要です。
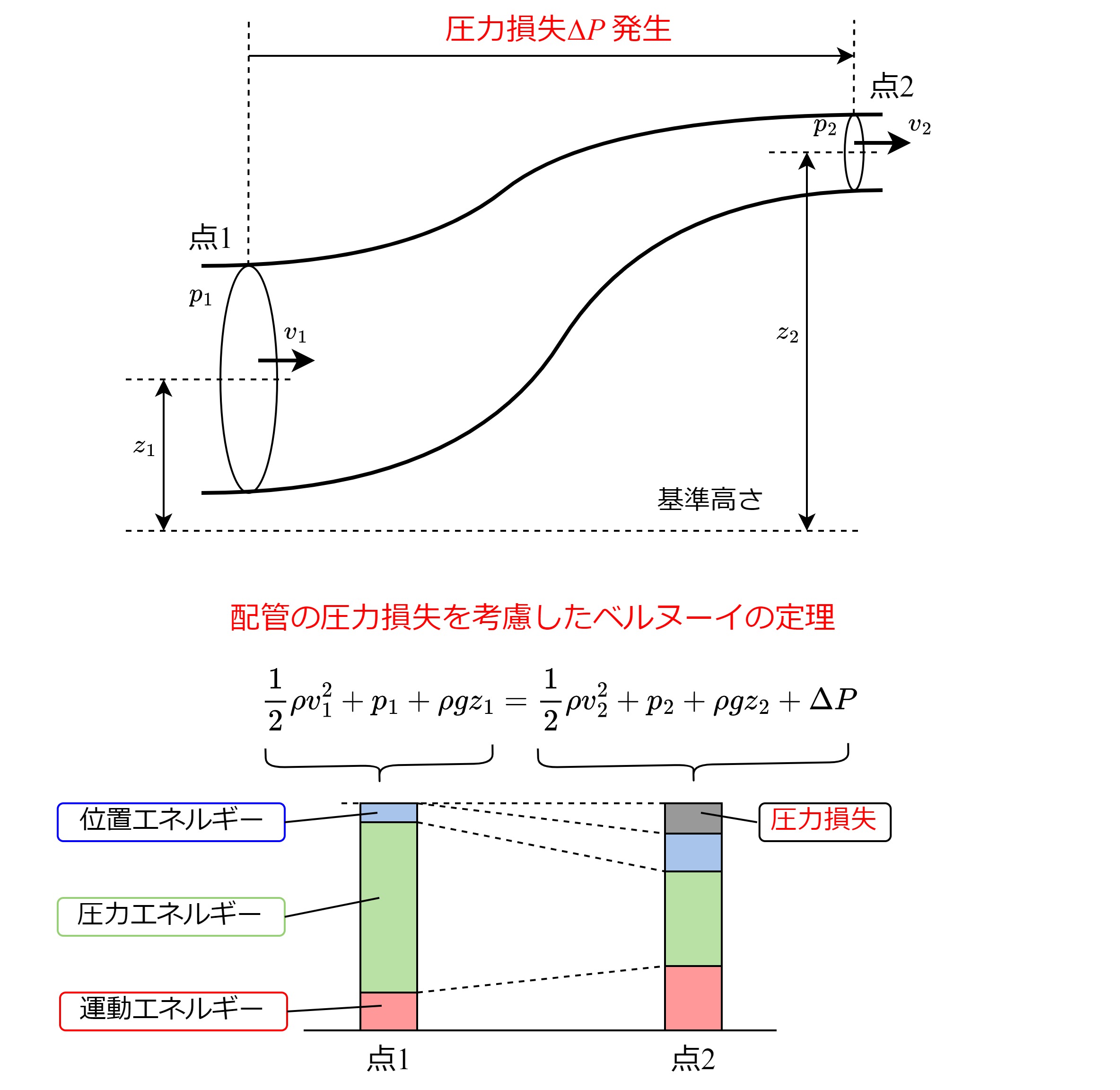
上の図のように配管の下流側におけるエネルギーの合計は、
上流側のエネルギーの合計から、圧力損失\(\Delta P\)を差し引いた値となります。
なお、配管の圧力損失\(\Delta P\)については別の記事で詳しく解説しています。
配管設計では「圧力損失」の考慮が必須ですが、「圧力損失」という言葉は聞いた事があっても、意味や計算方法がイマイチ分かり難いと思います。 本記事では、圧力損失の意味と計算方法について、初学者にも分かり易いように解説します。 […]
ベルヌーイの定理の応用(ピトー管・ベンチュリ管など)
ベルヌーイの定理を応用した機器として、流れの中に設置するだけで流速・流量を測定できるピトー管・ベンチュリ管・オリフィスなどが有名です。
測定原理やベルヌーイの定理の適用方法については別の記事で詳しく解説しています。
ピトー管についてはこちら↓
流体の速度を測る機器として「ピトー管」があります。航空機などに使われている事で有名です。 本記事ではピトー管の測定原理をベルヌーイの定理を使って説明します。 ピトー管とは ピトー管とは、流体の速度(以下、流速)を測定[…]
ベンチュリ管についてはこちら↓
配管流量を測定する機器として「ベンチュリ管」があります。ベルヌーイの定理を応用した機器で、流体力学の授業などでよく登場します。 本記事ではベンチュリ管の測定原理を図解と共に分かりやすく説明します。 ベンチュリ管とは […]
オリフィスについてはこちら↓
配管流量を測定する機器として「オリフィス流量計」があります。 ベルヌーイの定理を応用した機器で、流体力学の授業などでも登場します。 本記事ではオリフィス流量の測定原理を図解と共に分かりやすく説明します。 オリフィスとは […]
まとめ
流体力学で習う「ベルヌーイの定理」について解説しました。
ポイントをまとめます。
- ベルヌーイの定理とは「流体のエネルギー保存の法則」である
- ベルヌーイの定理が成立する条件下では、
流体の「運動」「圧力」「位置」のエネルギーの総和は一定となる - ベルヌーイの定理は以下の式で表される:
$$\frac{1}{2}\rho v^2 + p + \rho g z =一定$$ - ベルヌーイの定理は非粘性、非圧縮性、定常流、同一流線上、エネルギー損失・供給がないときに成立する
皆様の参考になれば幸いです。