オリフィス流量計は、配管内の流量を測定するための機器です。
そのシンプルな構造とベルヌーイの定理を応用した測定原理は、プラント設備や流体力学の分野で広く活用されています。
本記事では、オリフィス流量計の構造や測定原理を図解と共に分かりやすく解説し、メリット・デメリットや実際の使用例までを詳述します。本記事を読めば、オリフィス流量計の全体像が理解できます。
オリフィス流量計とは
オリフィス流量計は、配管内の流量を測定する機器の1つです。配管の中に「オリフィスプレート」と呼ばれる穴の開いた円盤を挿入し、流体の流れを部分的に絞る構造をしています。
絞る前後の圧力をそれぞれ測定し、この2点の圧力差から流量を算出するというのが、オリフィス流量計の基本原理です。これは「絞られた箇所は流速が速くなる代わりに、圧力が落ちる」という原理(ベルヌーイの定理)を利用したものです。(詳しくは後述します)
オリフィス流量計は、その構造のシンプルさから安価かつ保守が容易という大きなメリットがあり、プラント設備などで最も広く使われている流量計と言えます。
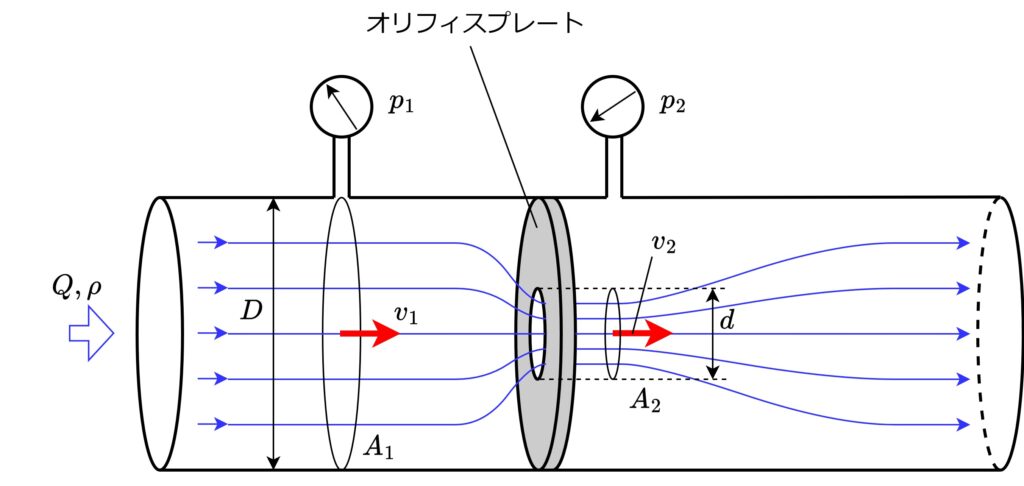
流体がオリフィスプレートを通過する際には、流れの剥離による圧力損失が生じます。
この特徴を利用し、オリフィスプレートは流量計として使う以外にも、意図的に減圧する・流量の制限を設けるといった使い方も可能です。このような目的で使用される物を「制限オリフィス」と言います。
オリフィス流量計の測定原理
前提知識:「ベルヌーイの定理」と「連続の式」
オリフィス流量計の測定原理を説明する前に、前提知識となる「ベルヌーイの定理」と「連続の式」について解説します。
「ベルヌーイの定理」とは?
ベルヌーイの定理とは「流体のエネルギー保存の法則」を示す定理で、以下の式で表されます。
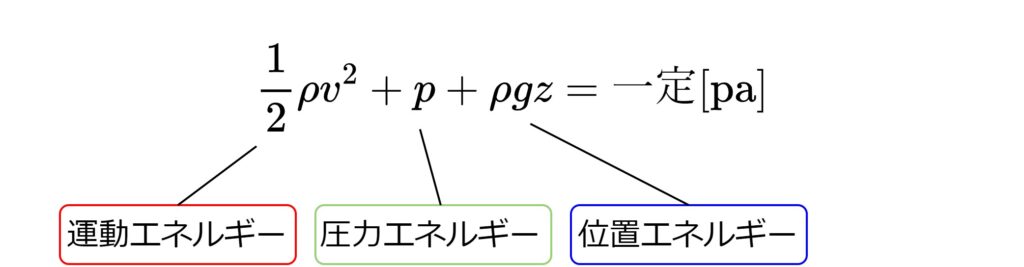
- \(\rho\):流体の密度 \(\rm{(kg/m^3)}\)
- \(v\):流速 \(\rm{(m/s)}\)
- \(p\):圧力 \(\rm{(pa)}\)
- \(g\):重力加速度 \(\rm{(m/s^2)}\)
- \(z\):高さ・水深 \(\rm{(m)}\)
運動エネルギー、圧力エネルギー、位置エネルギーは各々交換する事が可能で、その総和は一定になる、という流体力学において重要な定理です。
ただし、比較する2点が同一の流線上にある場合のみに適用可能、などの成立条件があります。ベルヌーイの定理については別の記事で詳しく解説しています。
ボールを空中に投げた時、位置エネルギーと運動エネルギーの総和は一定となり「エネルギー保存の法則」が成り立ちます。 これを流体に当てはめたのが「ベルヌーイの定理」です。 本記事ではベルヌーイの定理・考え方を初心者にもわかりや[…]
「連続の式」とは?
連続の式とは、「外部とのやりとりが無い限り、流体の質量流量はどの断面でも常に一定である」という定理です。
難しく聞こえますが簡単に言うと「流路が細い箇所ほど流速が大きくなる」という意味で、ホースで水を撒く際に先端をつぶすと流速が速くなるのと同じメカニズムです。
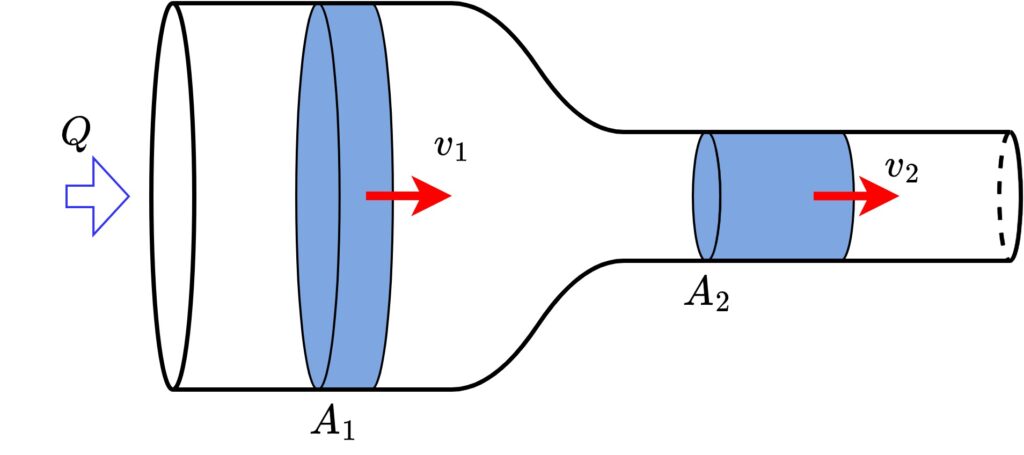
上の図のように流量\(Q\)が流れる管路において、断面積\(A_1\)の箇所の流速を\(v_1\)、断面積\(A_2\)の箇所の流速を\(v_2\)とすると、以下の式が成り立ちます。
$$Q=v_1 A_1=v_2 A_2$$
考えてみると当たり前に感じると思います。これが連続の式です。
オリフィス流量計の測定原理(図解)
上で紹介した「ベヌーイの定理」と「連続の式」を使ってオリフィス流量計の測定原理を解説します。
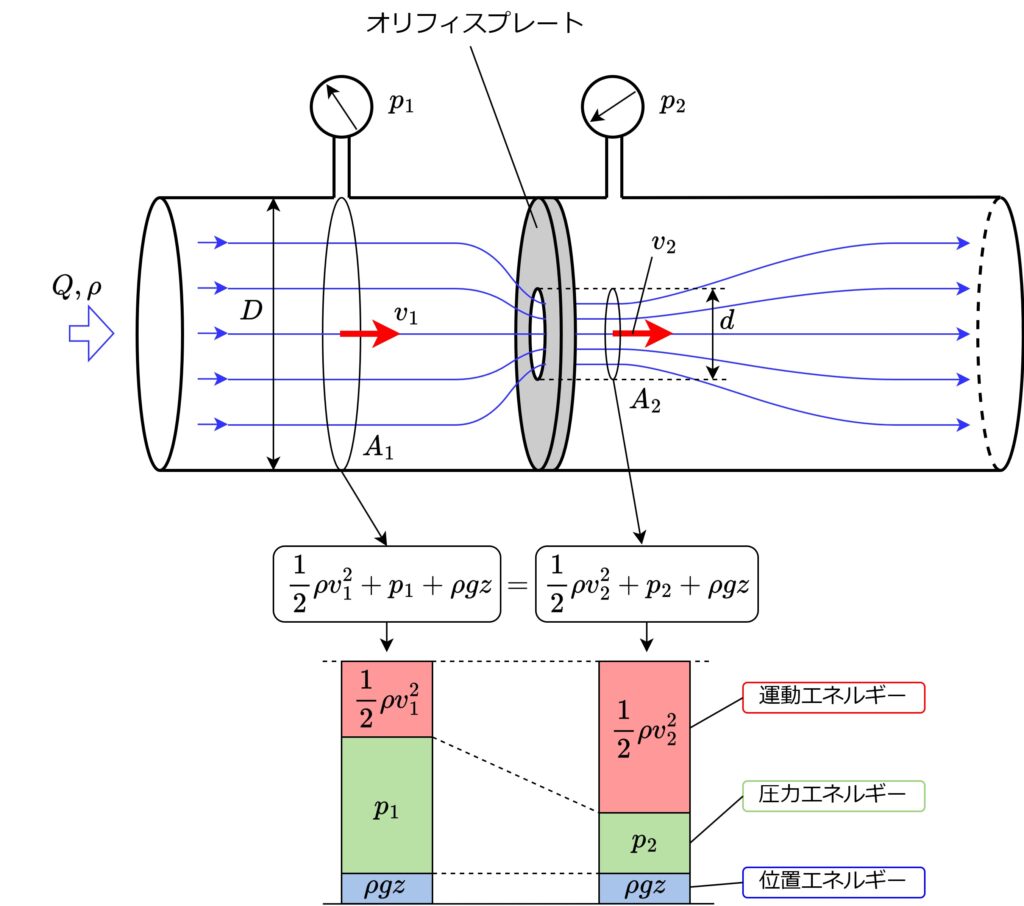
図のように流量\(Q\)、密度\(\rho\)の流体をオリフィスプレートに通した時、
絞る前 :内径\(D\)、断面積\(A_1\)、流速\(v_1\)、圧力\(p_1\)
絞った後:内径\(d\)、断面積\(A_2\)、流速\(v_2\)、圧力\(p_2\)
であるとすると、ベルヌーイの定理より以下の関係が成り立ちます。
$$\frac{1}{2}\rho v_1^2+p_1+\rho gz=\frac{1}{2}\rho v_2^2+p_2+\rho gz$$
絞る前後でエネルギーの配分は異なりますが総和は同じとなります。
絞った箇所では流速が速くなるため運動エネルギーが大きくなる分、圧力エネルギーが減る事でエネルギーの均衡が保たれます。また配管は水平であるとすると位置エネルギー\(\rho g z\)は左右で打ち消されます。
これを踏まえて上式を変形すると以下のようになります。
$$p_1-p_2=\frac{1}{2}\rho \left( v_2^2-v_1^2\right)$$
ここで連続の式:\(Q=v_1 A_1=v_2 A_2\)より、流速\(v_1,v_2\)を消去すると以下のようになります。
$$p_1-p_2=\frac{1}{2}\rho \left(\frac{1}{A_2^2}-\frac{1}{A_1^2}\right)Q^2$$
式変形すると、
$$Q=\frac{A_2}{\sqrt{1-\left(A_2/A_1\right)^2}} \times \sqrt{\frac{2\left(p_1-p_2\right)}{\rho}}$$
絞る前後の断面積と差圧から、流量\(Q\)が求められる事が分かります。これがオリフィス流量計の基本原理です。
なお実務においては絞り直径比\(\beta=(d/D=\sqrt{A_2/A_1})\)および流量係数\(C\)を用いて次の式を使います。
$$Q=C\frac{A_2}{\sqrt{1-\beta^4}} \times \sqrt{\frac{2\left(p_1-p_2\right)}{\rho}}$$
流量係数\(C\)とは理論上の流量に対し、圧力損失を考慮して実際の流量を表現する補正係数です。 オリフィス孔の厚みや形状によって異なりますが、流量係数\(C\)は0.61~0.98程度の値となります。
オリフィス流量計の特徴
オリフィス流量計の特徴をメリット・デメリットに分けて記載します。
メリット
- 薄板に穴を空けるシンプルな構造なので、製作が容易
- 可動部品が無いので保守が容易
- 他の流量計と比較して安価
デメリット
- オリフィス内径の先端(エッジ)が摩耗するため、固形物を含む流体に適さない
- 他の流量計と比較して圧力損失が大きい
- 流れに乱れがあると精度が落ちるため長い直管部分が必要。配管レイアウトに制限が出る。(上流は内径の5~80倍程度、下流は4~8倍程度の直管が必要)
オリフィス流量計はメリットが大きいので、プラント設備で流量を測定したい場合は、まずオリフィス流量計が検討されます。
なお、オリフィス流量計と同じ原理を利用した流量計として「ベンチュリ管流量計」や「フローノズル流量計」があります。これらを総称して差圧式流量計と呼びます。差圧式流量計の種類と特徴については、別の記事で詳しく解説しています。
流量を測定する機器の一つに「差圧式流量計」があります。 差圧式流量計にはオリフィス流量計、ベンチュリ管流量計、フローノズル流量計などの種類があり、用途によって使い分けられます。 本記事では差圧式流量計の選定材料として、それ[…]
オリフィス流量計の使用例
プラント設備などで実際に使われるオリフィス流量計の例です。
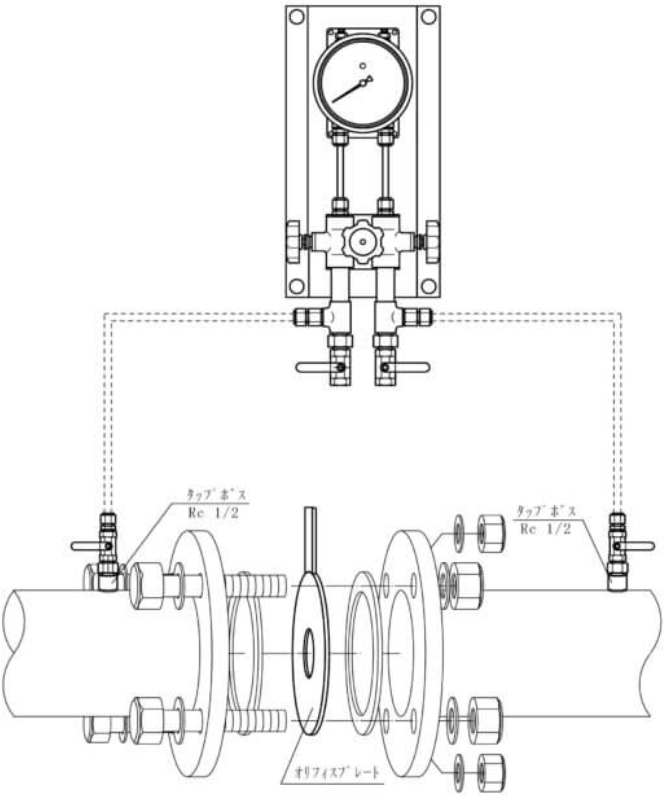
配管フランジの間にオリフィスプレートを挟み込み、前後のタップボスがら圧力を検出して流量を測定します。保守はオリフィスプレートの定期的な点検・交換で済みます。
まとめ
ベルヌーイの定理を利用したオリフィス流量計の測定原理を解説しました。
ポイントをまとめます。
- オリフィス流量計は穴の空いた薄板(オリフィスプレート)により管路の途中が絞られた構造をしており、絞る前後の差圧から「流量」を算出することができる。
- 「絞られた箇所は流速が速くなる代わりに圧力が下がる」というベルヌーイの定理を利用している。
- 流量\(Q\)は以下で計算できる:
$$Q=C\frac{A_2}{\sqrt{1-\beta^4}} \times \sqrt{\frac{2\left(p_1-p_2\right)}{\rho}}$$
(\(C\):流量係数、\(\beta\):絞り直径比、\(A_1,A_2\):絞る前,後の断面積、\(p_1,p_2\):絞る前,後の圧力、\(\rho\):流体密度) - 「構造がシンプルで製作・保守が容易、かつ安価」というメリットがある一方で、「固形物に弱い、圧力損失が大きい、配管レイアウトに制限が出る」というデメリットもある。
- メリットが大きいためプラント設備などでは流量計としてオリフィス流量計がまず検討される。
皆様の参考になれば幸いです。








