配管設計では「圧力損失」の考慮が必須ですが、
「圧力損失」という言葉は聞いた事があっても、
意味や計算方法がイマイチ分かり難いと思います。
本記事では、圧力損失の意味と計算方法について、
初学者にも分かり易いように解説します。
圧力損失とは何か
圧力損失とは「エネルギー損失」を意味する
配管を流れる流体は、常に配管壁面からの摩擦抵抗を受けながら進んでいます。
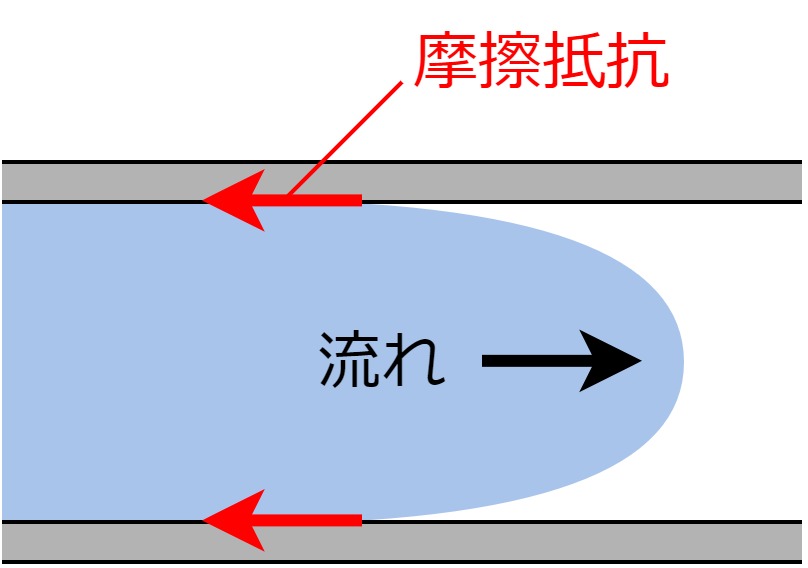
摩擦抵抗を受ければ当然、エネルギーを損失します。
このエネルギー損失の事を「圧力損失」と言います。
エネルギー損失を圧力損失と呼ぶことに違和感があるかもしれませんが、
流体の世界ではエネルギーを「圧力」に換算して計算する事が多いです。
運動エネルギーや位置エネルギーも「圧力」に換算して計算されます。
圧力損失による不具合の例
圧力損失とはエネルギー損失を意味するので、
この考慮を怠ると末端側でエネルギーが不足し、以下のような不具合が発生します。
- 流速が遅い、流れない
- シリンダーなどの機器の動作が遅い
圧力損失は正しく理解し、事前に見積もった上で設計する事が必要です。
圧力損失の計算方法
圧力損失はダルシー・ワイスバッハの式で計算する
圧力損失は以下のダルシー・ワイスバッハの式で計算します。
$$\Delta P=\lambda \frac{L}{D}\frac{\rho v^2}{2}$$
- \(\Delta P\):圧力損失 \(\rm{(Pa)}\)
- \(\lambda\):管摩擦係数 \(\rm{(無次元)}\)
- \(L\):配管長さ \(\rm{(m)}\)
- \(D\):配管内径 \(\rm{(m)}\)
- \(\rho\):流体の密度 \(\rm{(kg/m^3)}\)
- \(v\):流速 \(\rm{(m/s)}\)
よく似た式に「ファイニングの式」がありますが、
上式の管摩擦係数\(\lambda\)が\(4f\)に置き換わっただけで、あとは同じです。
ダルシー・ワイスバッハの式(\(\lambda\)を使う)なのか、
ファイニングの式(\(4f\)を使う)なのかで摩擦係数の数字が4倍違いますので、
間違わないように注意してください。
以下に、ダルシー・ワイスバッハの式の各係数の算出方法を解説します。
流速の求め方
流速\(v\)は以下の式で求めます。
$$v=\frac{Q}{A}=\frac{Q}{\frac{\pi}{4}D^2}$$
- \(v\):流速 \(\rm{(m/s)}\)
- \(Q\):流量 \(\rm{(m^3/s)}\)
- \( A\):配管断面積 \(\rm{(m^2)}\)
- \( D\):配管内径 \(\rm{(m)}\)
流量\(Q\)は\(\rm{m^3/min}\)や\(\rm{L/min}\)で表される事も多いので、
単位換算に注意してください。
管摩擦係数の求め方
管摩擦係数\(\lambda\)は、配管壁面/流体の間の摩擦係数を意味し、
「レイノルズ数」と「配管内側の表面粗さ」で決まります。
管摩擦係数の求め方を順を追って解説します。
まずレイノルズ数を求めて、層流or乱流を判定する
管摩擦係数の計算式は層流 or 乱流で異なるので、
まずはレイノルズ数\(Re\)を求めて流れの状態を把握します。
レイノルズ数は以下の定義式で求めます。
$$Re=\frac{\rho v \ell}{\mu}=\frac{v \ell}{\nu}$$
- \(\rho\):流体の密度 \(\rm{(kg/m^3)}\)
- \(v\):流体の速度 \(\rm{(m/s)}\)
- \(\ell\):代表長さ※ \(\rm{(m)}\)
- \(\mu\):流体の粘度 \(\rm{(Pa・s)}\)
- \(\nu\):流体の動粘度 \(\rm{(m^2/s)}\)
※配管の場合、代表長さ\(\ell\)は配管内径となります。
レイノルズ数は流体の「粘性力と慣性力の比」を表す物理量で、
この大小で層流or乱流を判定できます。
レイノルズ数と層流・乱流については以下の記事で詳しく解説しています。
流体力学や配管設計では「レイノルズ数」が頻繁に登場します。 本記事ではレイノルズ数の求め方・物理的な意味を解説していきます。 レイノルズ数とは何か レイノルズ数とは流れの状態を知る上で重要な数値であり、「流体の粘性力[…]
管摩擦係数の求め方(層流の場合)
\(Re<2,300\)のとき流れは「層流」となり、
管摩擦係数\(\lambda\)は以下の式で計算できます。
$$\lambda=\frac{64}{Re}$$
層流の場合、管摩擦係数は配管内側の表面粗さにはよらず、
レイノルズ数で決まります。
ただし、配管設計ではほとんどの場合で「乱流」となるので、
上の式で管摩擦係数を求める事は少ないです。
管摩擦係数の求め方(乱流の場合)
\(Re>4,000\) のとき流れは「乱流」となります。
乱流の場合、管摩擦係数\(\lambda\)の計算式は様々なものが提案されていますが、
以下のコールブルックの式で求める事が多いです。
$$\frac{1}{\sqrt{\lambda}}=-2\ {\rm log}\left( \frac{\varepsilon}{3.71d} +\frac{2.51}{Re\sqrt{\lambda}}\right)$$
- \(\lambda\):管摩擦係数 \(\rm{(無次元)}\)
- \(\varepsilon\):配管内側の表面粗さ(凹凸の平均高さ)
- \(d\):配管内径
- \(Re\):レイノルズ数\(\rm{(無次元)}\)
これをグラフ化したものがムーディ線図で、
管摩擦係数\(\lambda\)はほとんどの場合、このムーディ線図で求めます。
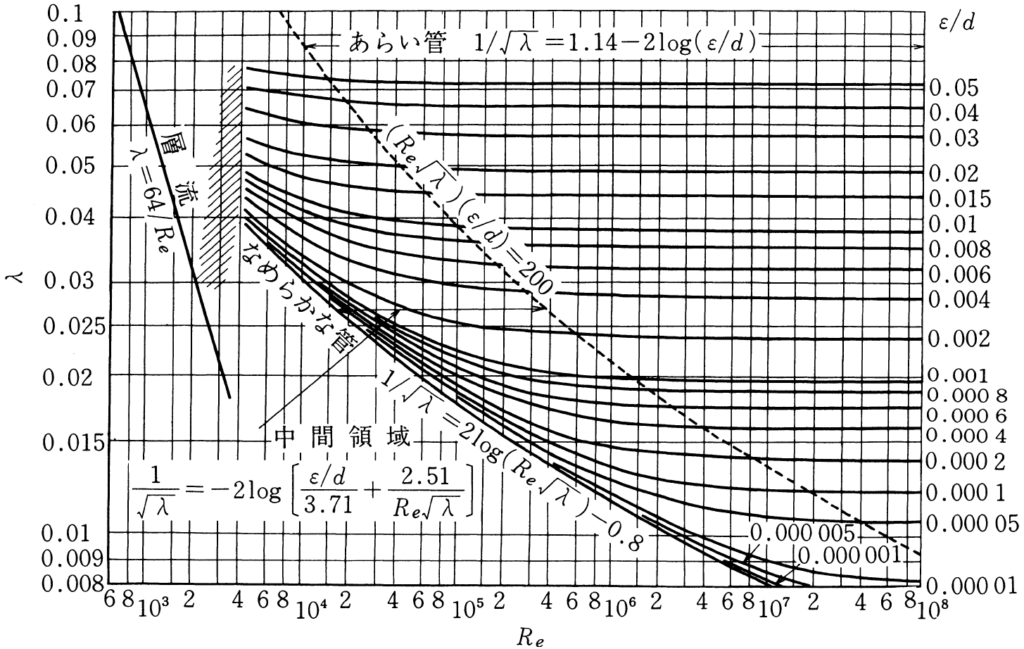
配管内側の表面粗さ\(\varepsilon\)の目安は以下の通りです。
| 配管の種類 | 表面粗さ\(\varepsilon \rm{(mm)}\) |
|---|---|
| 引抜管 | 0.0015 |
| 市販鋼管・錬鉄管 | 0.045 |
| 鋳鉄管 | 0.26 |
管摩擦係数の求め方とムーディ線図の見方については、
以下の記事で詳しく解説しています。
配管の抵抗・圧力損失を求める際には「管摩擦係数」が登場します。 本記事では管摩擦係数の求め方と、有名な「ムーディ線図」の使い方について詳しく解説します。 管摩擦係数とは 配管内を流れる流体は、常に配管壁面からの摩擦抵[…]
筆者の経験上、管摩擦係数は0.015~0.025程度の値になる事が多いです。
(もちろん、条件によって値は異なります)
配管長さの求め方
配管のレイアウト図から全体の長さを足していきます。
このとき、足して良いのは同じ径の配管だけです。
径が異なる配管は流速が異なるので、
圧力損失を別々で計算して最後に足し合わせます。
配管内径の求め方
圧力損失を厳密に計算する場合は配管の「内径」を求めます。
JISの規格表などから、内径を直接読み取るか、
内径=外形-肉厚×2で計算します。
【JIS規格表の参考ページ】
SGP管の規格表はこちら
STPG管の規格表はこちら
その他配管の規格表はこちらから調べられます
密度の求め方
常温の水であれば998 kg/m3(20℃)で計算します。
厳密には温度によって密度は変化しますが、
水の場合は密度一定として計算しても精度に問題はありません。
一方、エアー・ガスなどの気体の場合は、
温度・圧力による密度の変化を考慮する必要があります。
$$\rho=\rho_0 \times \frac{273}{273+t} \times \frac{P+0.10133}{0.10133}$$
- \(\rho\):密度 \(\rm{(kg/m^3)}\)
- \(\rho_0\):標準状態\(\rm{(0℃、1気圧)}\)での密度 \(\rm{(kg/m^3)}\)
- \(t\):温度 \(\rm{(℃)}\)
- \( P\):圧力 \(\rm{(MPa)}\)
以上の方法で、直管部分の圧力損失を計算できます。
曲がり・バルブ(複雑形状)の圧力損失の求め方
直管部分の圧力損失は上記までの方法で計算できますが、
道中にある曲がり・弁などの直管以外の箇所は別の方法で計算します。
直管では摩擦抵抗によって圧力損失が生じるのに対し、
流路が複雑な箇所では、渦の発生・流れの剥離などによるエネルギー損失も生じるためです。
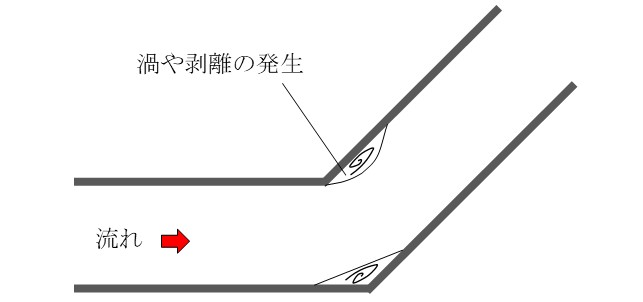
複雑形状での圧力損失の計算方法は2通りあります。
- 損失係数\(\zeta\)を使う方法
- 相当長さ(等価管長)\(L_e\)を使う方法
どちらかの方法を使って圧力損失を求め、
最後に直管の圧力損失に足し合わせることで配管全体の圧力損失を求めます。
複雑形状の圧力損失の計算方法については別の記事で詳しく解説しています。
様々な流路の損失係数ζ・相当長さ(等価管長)\(L_e\)をまとめた保存版になりますので
ぜひ参考にしてください。
配管の圧力損失を計算する際、曲がりやバルブ類などの複雑形状については、損失係数や相当長さ(等価管長)を使います。 本記事では損失係数・相当長さについて、考え方と計算方法を解説します。 文献から各種係数をまとめていますので、[…]
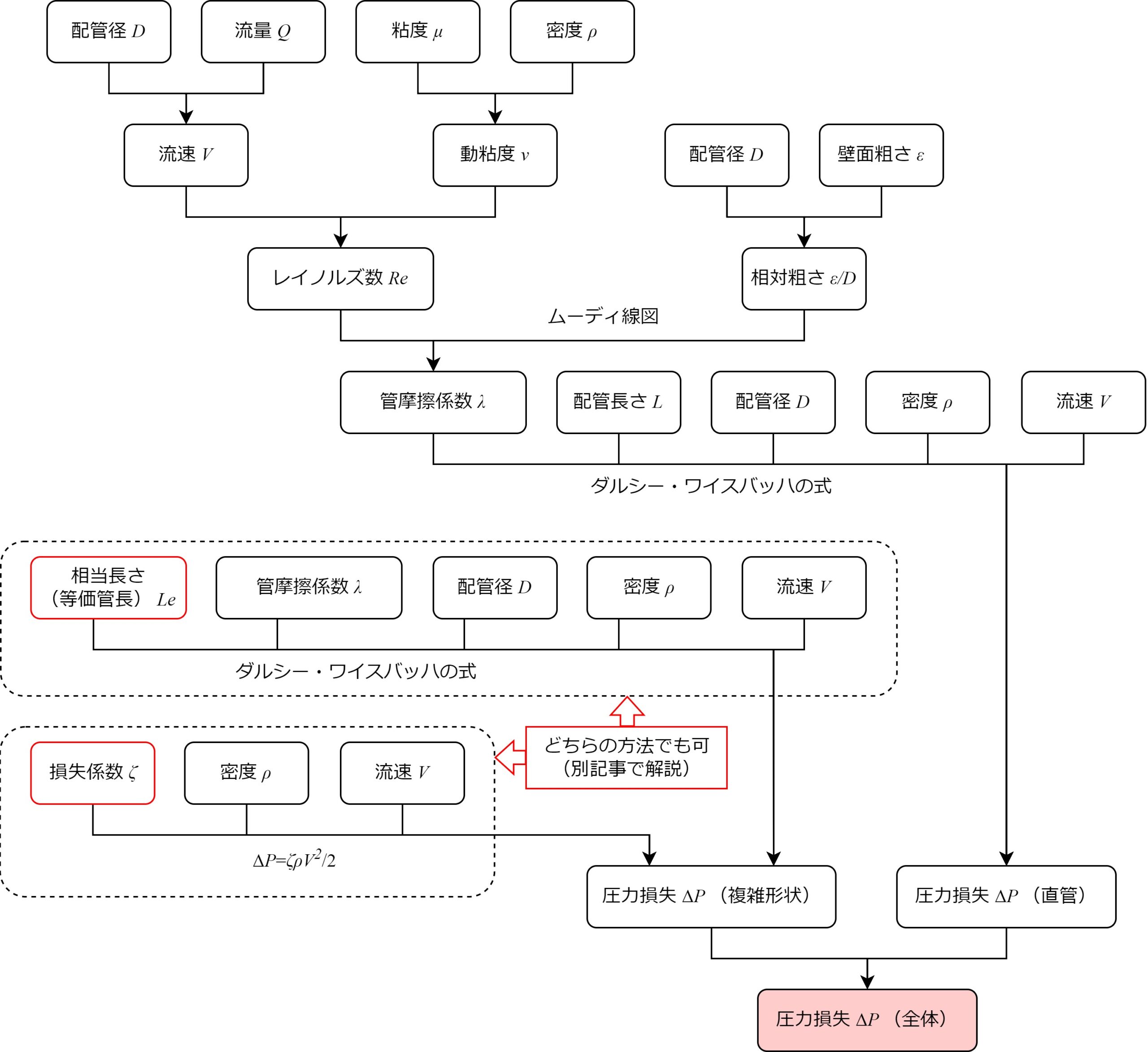
圧力損失の計算フロー(図解)
圧力損失の計算は手順が長いので、混乱しないよう計算フローを図にまとめました。
必要な係数・物性値が多いですが、各々の求め方は難しくありませんので、
一つ一つ着実に計算していきましょう。
圧力損失を計算する際の注意点
圧力損失に一番効くのは「流速」
ダルシー・ワイスバッハの式を見て分かる通り、
圧力損失は流速の2乗に比例して大きくなりますので、
圧力損失に一番効く(支配する)のは流速と言えます。
参考までに各流体での一般的な流速を示します。
これらを標準流速(基準流速)と言います。
- 水 1.5~2m/s
- エアー 15~20m/s
- 蒸気 20~30m/s
標準流速を上回る場合は、圧力損失が過多になる事が多いので注意が必要です。
逆に言えば、標準流速以下の流速で設計していれば、
圧力損失で困ることはほぼありません。
圧力損失を減らす方法については別の記事で解説しています。
配管の圧力損失が大きいと、「必要な流量が出ない」「機器の動作が遅い」などの不具合が発生します。 本記事では、圧力損失が大きくなる主な原因と、圧力損失を減らす具体的な方法を解説します。 圧力損失が大きくなる原因 […]
計算結果は参考程度と捉え、設計者で安全率をかけよう
圧力損失の計算方法を解説しましたが、
計算結果はオーダーを把握するための参考値と捉えるのが無難です。
実際の圧力損失を計算でズバリ当てるのは、以下のような理由から至難の業です。
- 管摩擦係数(壁面粗さ)は配管材質から経験則で決める事
- バルブ等の損失係数・相当長さは型式によって異なる事
- 流体の物性値は温度・圧力・混入物によって変化する事
参考までに私の場合は、計算結果から1.3~1.5倍程度の安全率を掛けて、
圧力損失を多めに見積もってポンプ・機器を選定しています。
設計者側で安全率をかけておけば、後から配管ルート微修正・バルブ追加などの
設計の変更にも対応し易いので安心です。
圧縮空気(エアー)は体積の扱いに注意
気体は温度・圧力によって体積が変化します。
以下のボイル・シャルルの法則が有名ですね。
$$\frac{PV}{T}=(一定)$$
(\(P\):圧力、\(V\):体積、\(T\):絶対温度)
ダルシー・ワイスバッハの式で使う「密度」と「流速」は流体の体積によって変わるので、
何\(\rm{MPa}\)、何 \(\rm{℃}\)の前提での数値なのかを考慮しましょう。
特に圧縮空気(エアー)の場合は注意が必要で、
以下のような事象により計算と実測が大きく異なる事があります。
圧力損失により気体の圧力が低下する
↓
圧力の低下により気体が膨張し、流速が想定より速くなる
↓
流速が想定より速いので、圧力損失も想定より大きくなる
↓
以下繰り返し(負のループ)
圧縮空気の場合、圧力損失の計算精度を上げる例として、
配管全長をある一定間隔に区切る(エリア分けする)方法があります。
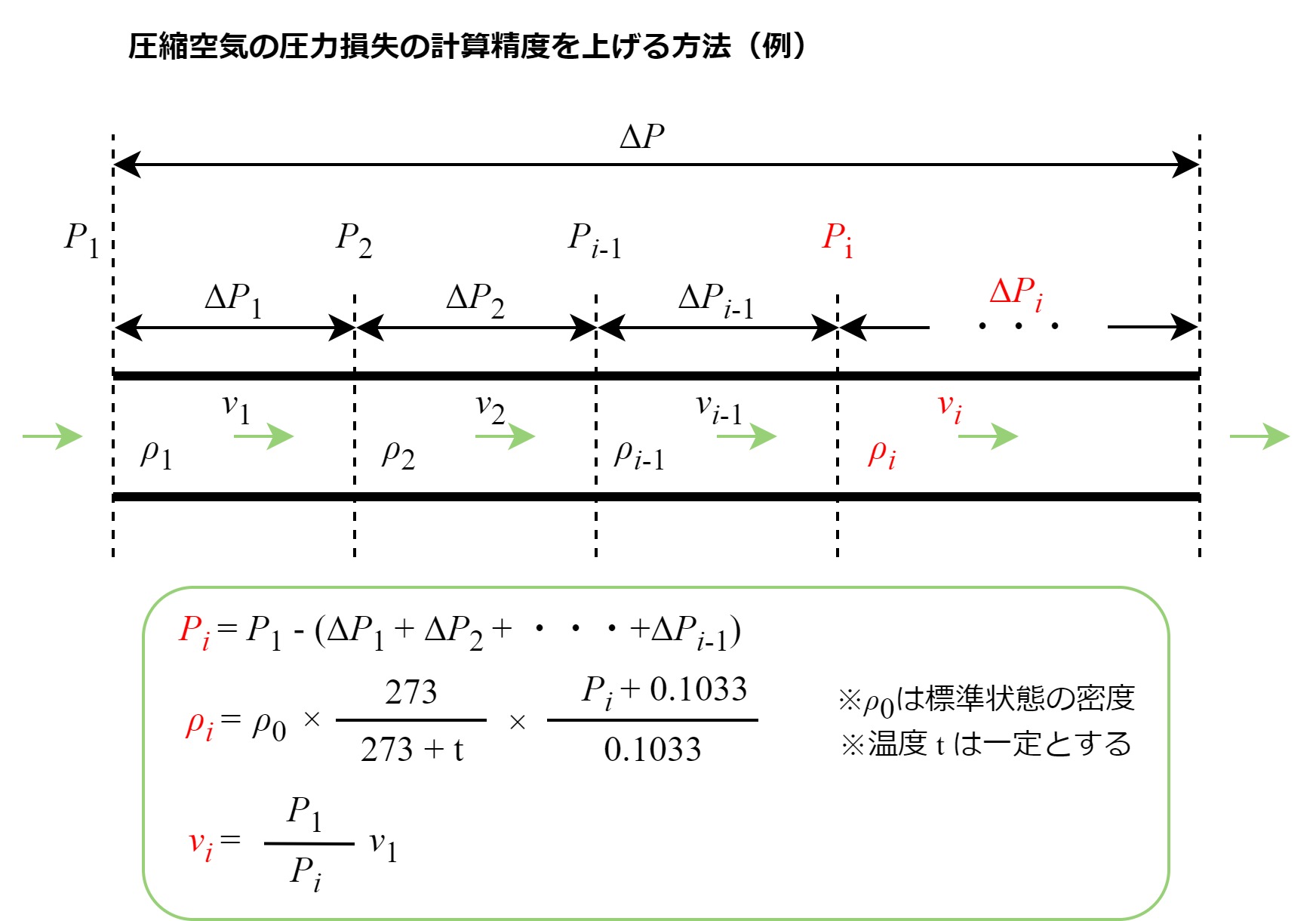
分割した各エリアの圧力損失\(\Delta P_i\)の合計が全体の圧力損失\(\Delta P\)になります。
各エリア入口の圧力\(P_i\)を基に、各エリア内での密度\(\rho_i\)と流速\(v_i\)を都度求めて
圧力損失\(\Delta P_i\)を計算することで、上記のような体積変化を考慮する事ができます。
手間の掛かる方法に見えますがExcelを使えば割と簡単に計算できます。
まとめ
圧力損失の意味と計算方法、注意点について解説しました。
ポイントをまとめます。
- 圧力損失とは配管壁面からの摩擦によるエネルギー損失を意味する
- 圧力損失は以下のダルシー・ワイスバッハの式で計算する$$\Delta P=\lambda \frac{L}{D}\frac{\rho v^2}{2}$$
- 管摩擦係数\(\lambda\)は「レイノルズ数」と「配管内側の表面粗さ」で決まり、ムーディ線図から読み取る
- 複雑形状の圧力損失は「損失係数を使う方法」か「相当長さを使う方法」のどちらかで計算する
皆様の参考になれば幸いです。