配管の抵抗・圧力損失を求める際には「管摩擦係数」が登場します。
本記事では管摩擦係数の求め方と、
有名な「ムーディ線図」の使い方について詳しく解説します。
管摩擦係数とは
配管内を流れる流体は、常に配管壁面からの摩擦抵抗を受けます。
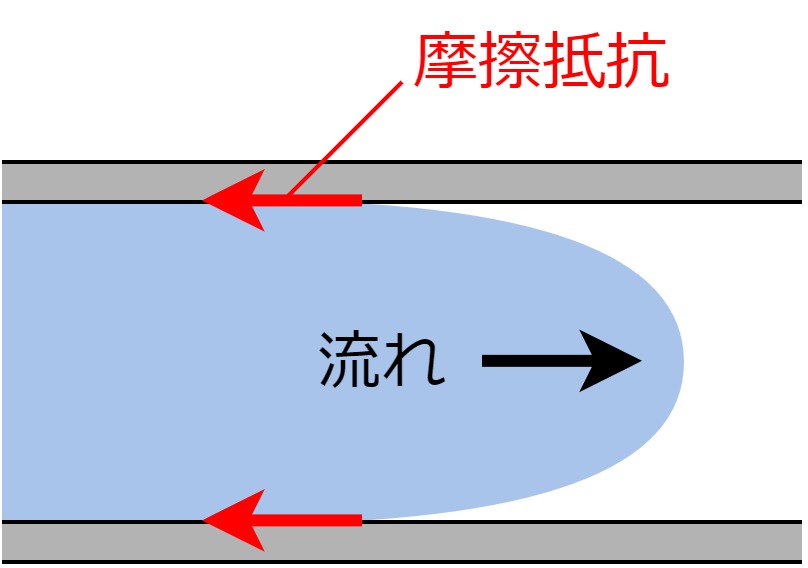
摩擦抵抗によるエネルギー損失は「圧力損失」と言い換えられ、
以下の式で計算されます(ダルシー・ワイスバッハの式)。
この式の係数\(\lambda\)が「管摩擦係数」になります。
$$\Delta P=\lambda \frac{L}{D}\frac{\rho V^2}{2}$$
- \(\Delta P\):圧力損失 \(\rm{(Pa)}\)
- \(\lambda\):管摩擦係数 \(\rm{(無次元)}\)
- \(L\):配管長さ \(\rm{(m)}\)
- \(D\):配管内径 \(\rm{(m)}\)
- \(\rho\):流体の密度 \(\rm{(kg/m^3)}\)
- \(V\):流速 \(\rm{(m/s)}\)
圧力損失の計算方法と注意点については、
以下の記事で詳しく解説しています。
配管設計では「圧力損失」の考慮が必須ですが、「圧力損失」という言葉は聞いた事があっても、意味や計算方法がイマイチ分かり難いと思います。 本記事では、圧力損失の意味と計算方法について、初学者にも分かり易いように解説します。 […]
ダルシー・ワイスバッハの式を見て分かるように、
管摩擦係数は圧力損失(=エネルギー損失)に掛け算で効きます。
従って管摩擦係数の見積もりが不適切で2倍間違えて計算した場合、
圧力損失も2倍間違う事になり設計全体に影響が出ますので、
管摩擦係数は正しく求める事が重要です。
管摩擦係数は「配管内側の表面粗さ」と、「流体のレイノルズ数」で決まります。
以下に管摩擦係数の求め方を詳しく解説します。
管摩擦係数の計算方法
まずレイノルズ数を求めて、層流 or 乱流を判定する
管摩擦係数の計算式は層流 or 乱流で異なるので、
まずはレイノルズ数Reを求めて流れの状態を把握します。
レイノルズ数は以下の定義式で求めます。
$$Re=\frac{\rho V L}{\mu}=\frac{VL}{\nu}$$
- \(\rho\):流体の密度 \(\rm{(kg/m^3)}\)
- \(V\):流体の速度 \(\rm{(m/s)}\)
- \(L\):代表長さ \(\rm{(m)}\)
- \(\mu\):流体の粘度 \(\rm{(Pa・s)}\)
- \(\nu\):流体の動粘度 \(\rm{(m^2/s)}\)
レイノルズ数とは流れの状態(層流 or 乱流)を知るための指数で、
流体の「粘性力と慣性力の比」を表しています。
レイノルズ数については以下の記事で詳しく解説しています。
流体力学や配管設計では「レイノルズ数」が頻繁に登場します。 本記事ではレイノルズ数の求め方・物理的な意味を解説していきます。 レイノルズ数とは何か レイノルズ数とは流れの状態を知る上で重要な数値であり、「流体の粘性力[…]
管摩擦係数の計算式(層流の場合)
\(Re<2,300\)のとき流れは「層流」となり、
管摩擦係数\(\lambda\)は以下の式で計算できます。
$$\lambda=\frac{64}{Re}$$
層流の場合、管摩擦係数は配管内側の表面粗さにはよらず、
レイノルズ数で決まります。
ただし、配管設計ではほとんどの場合で「乱流」となるので、
上の式で管摩擦係数を求める事は少ないです。
管摩擦係数の計算式(乱流の場合)
\(Re>4,000\)のとき流れは「乱流」となります。
乱流状態の管摩擦係数は、管の材質に基づき「平滑管」と「粗面管」に
場合分けされ、各々で計算式が異なります。
- 平滑管:ガラス管、アクリル管、銅管など
- 粗面管:鋼管、鋳鉄管など
平滑管とは名前の通り、表面が滑らかで粗さを無視できる配管のことです。
対して粗面管は粗さを無視できない配管です。
プラントの配管設計では鋼管を使う事が多いので、
ほとんどの場合で粗面管として計算します。
平滑管の場合
乱流状態かつ平滑管の場合、様々な管摩擦係数の計算式が提案されており、
レイノルズ数の適用範囲によって以下のように使い分けられます。
ブラジウスの式(\(Re:3\times 10^3 \sim 10^5\))
$$\lambda=0.3164 Re^{-0.25}$$
ニクラゼの式(\(Re:10^5 \sim 3\times 10^6\))
$$\lambda=0.0032+0.221 Re^{-0.237}$$
カルマンの式(\(Re:3\times 10^3 \sim 10^6\))
$$\frac{1}{\sqrt{\lambda}}=2.0\ {\rm log}(Re \sqrt{\lambda})-0.8$$
この式は両辺に\(\lambda\)がある陰的な方程式なので、直接解く事はできず、
Excelのゴールシーク機能などを用いて計算します。
粗面管の場合
乱流状態かつ粗面管の場合、
管摩擦係数\(\lambda\)は以下のコールブルックの式
(コールブルック・ホワイトの式とも言う)で計算します。
$$\frac{1}{\sqrt{\lambda}}=-2\ {\rm log}\left( \frac{\varepsilon}{3.71d} +\frac{2.51}{Re\sqrt{\lambda}}\right)$$
- \(\lambda\):管摩擦係数 \(\rm{(無次元)}\)
- \(\varepsilon\):配管内側の表面粗さ(凹凸の平均高さ)
- \(d\):配管内径
- \(Re\):レイノルズ数
この式は両辺に\(\lambda\)がある陰的な方程式なので、直接解く事はできず、
以下のいずれかの方法を選択する事になります。
- 数値計算を用いる(Excelのゴールシーク機能など)
- 陽的な近似式を用いる
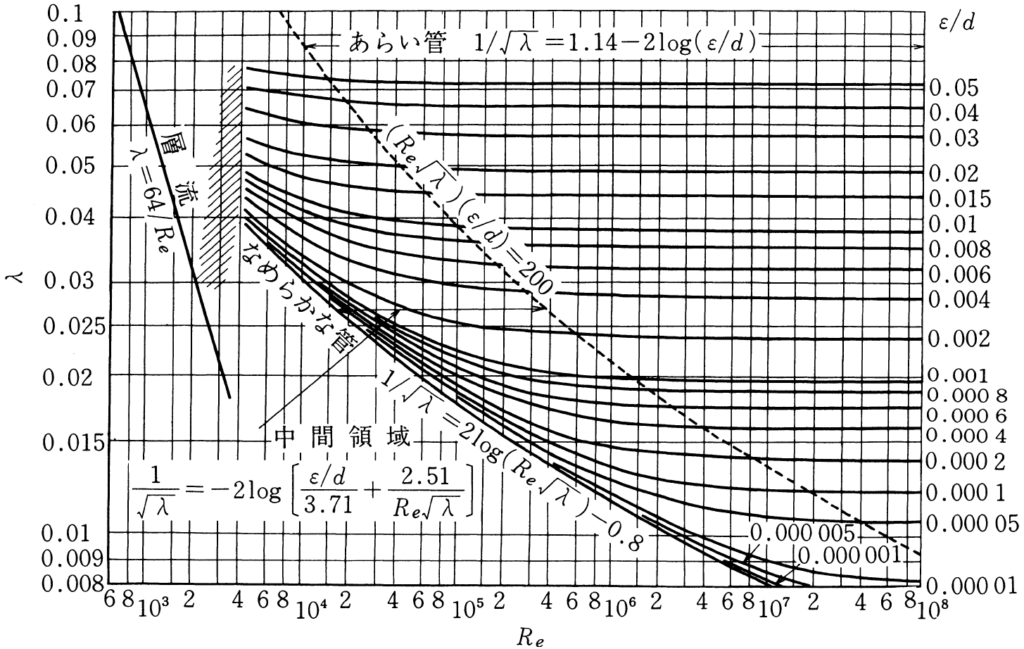
- 式をグラフ化した「ムーディ線図」から読み取る
実用上は③のムーディ線図(下の図)から読み取る方法が一般的です。
ムーディ線図の使い方は後述します。
ムーディ線図の使い方
乱流かつ粗面管の条件において、管摩擦係数はムーディ線図から読み取ることが一般的です。
ムーディ線図の使い方を順番に解説します。
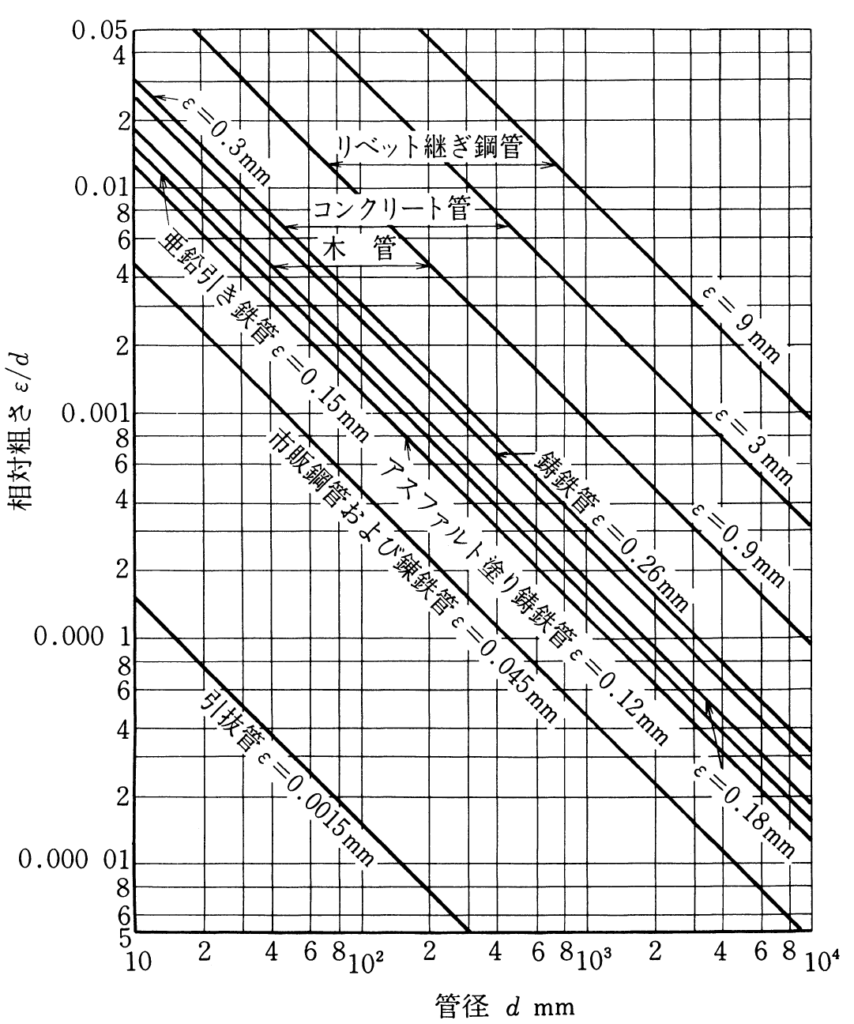
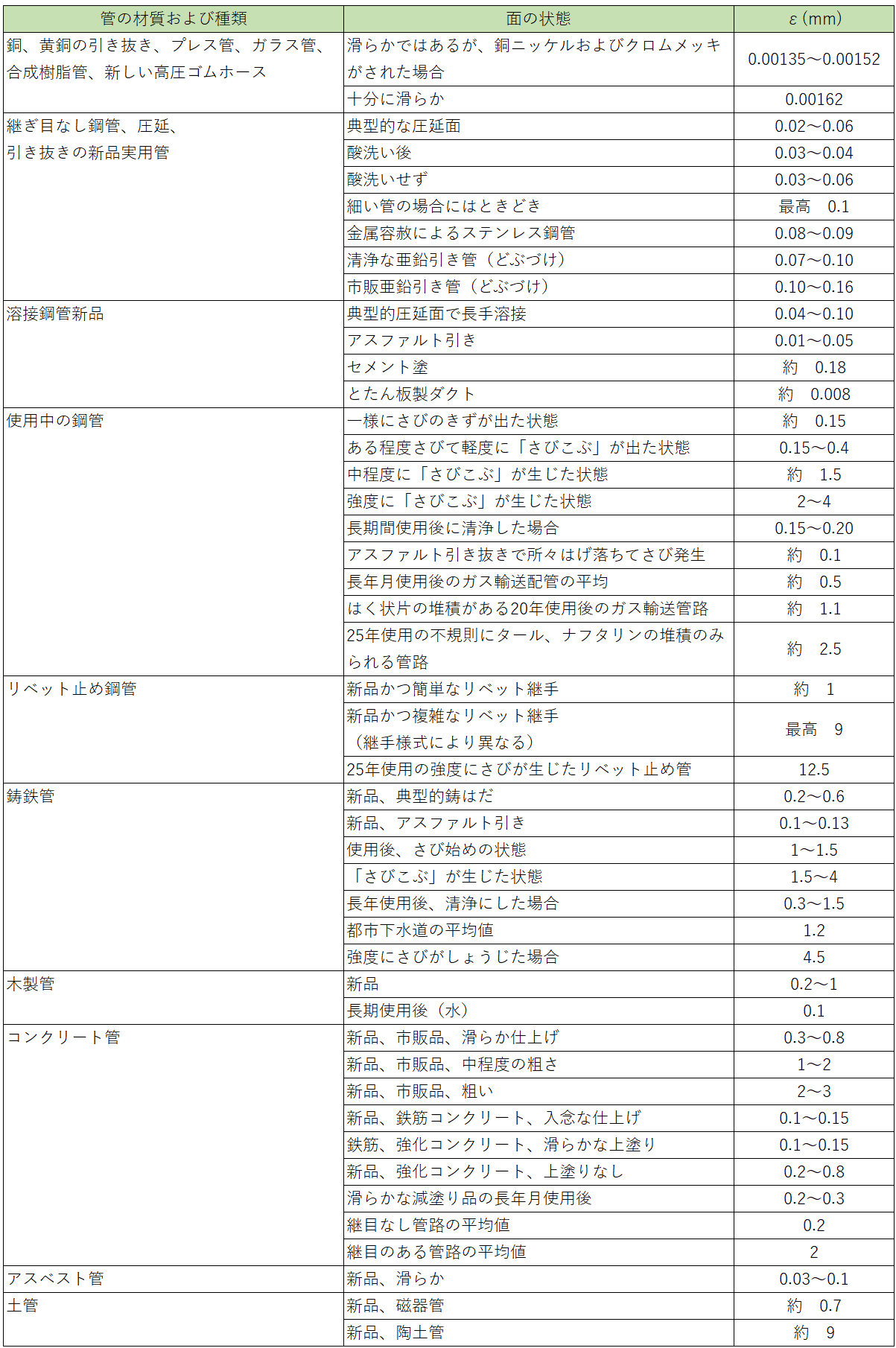
管路の相対粗さを求める
管の内径\(d\)と表面粗さ\(\varepsilon\)の比である、「相対粗さ\(\varepsilon/d\)」を求めます。
相対粗さ\(\varepsilon/d\)の求め方は主に以下の2通りです。
- ムーディが示した図(実用管の相対粗さ)から直接読み取る
- リヒターが示した数値表(実用管の等価粗さ)の\(\varepsilon\)を\(d\)で割る
どちらの方法でも結果に大差はありませんので、使いやすい方で問題ありません。
レイノルズ数を求める
\(Re=VL/\nu\) でレイノルズ数を求めます。
(\(V\):流速\(\rm{(m/s)}\)、\(L\):代表長さ\(\rm{(m)}\)、\(\nu\)動粘度\(\rm{(m^2/s)}\))
ムーディ線図から管摩擦係数を読み取る
ムーディ線図の右側縦軸を見ながら、先ほど求めた相対粗さ\(\varepsilon/d\)に相当する線を追います。
この線と上で求めたレイノルズ数が交差する点において、
左側縦軸を読み取った数値が、求めるべき管摩擦係数\(\lambda\)です。
例として、相対粗さ\(\varepsilon/d=0.001\)、レイノルズ数\(Re=6\times 10^5\)
の時のムーディ線図の読み取り方を、手順①~③に分けて記載しました。
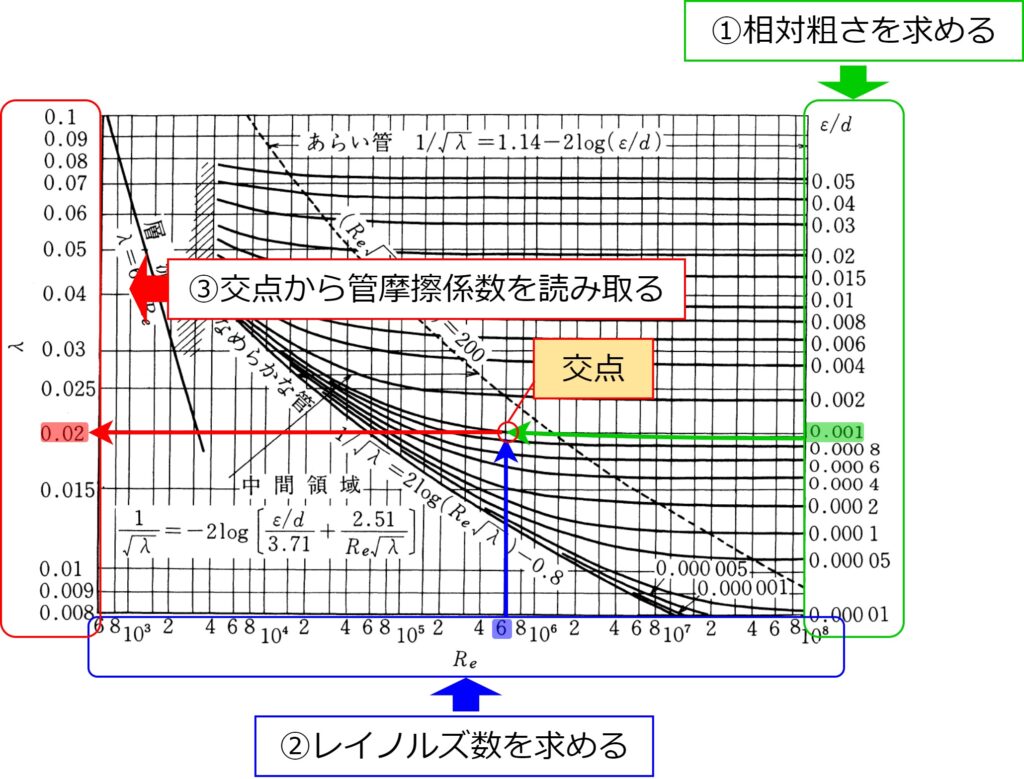
筆者の経験上、水や空気を鋼管で流すプラント配管においては、
ムーディ線図で求めた管摩擦係数は0.015~0.025程度の値になる事が多いです。
(もちろん、条件によって値は異なります)
管摩擦係数の計算式一覧表
各条件における、管摩擦係数の計算方法を表にまとめます。
| 流れ | 管路 | レイノルズ数 | 計算式 |
|---|---|---|---|
| 層流 | 粗さに よらない | \(Re<2,300\) | $$\lambda=\frac{64}{Re}$$ |
| 乱流 | 平滑管 | \(3\times 10^3\leq Re \leq 10^5\) | ブラジウスの式 $$\lambda=0.3164 Re^{-0.25}$$ |
| 乱流 | 平滑管 | \( 10^5\leq Re \leq 3\times 10^6\) | ニクラゼの式 $$\lambda=0.0032+0.221 Re^{-0.237}$$ |
| 乱流 | 平滑管 | \(3\times 10^3\leq Re \leq 10^6\) | カルマンの式 $$\frac{1}{\sqrt{\lambda}}=2.0\ {\rm log}(Re \sqrt{\lambda})-0.8$$ |
| 乱流 | 粗面管 | \(Re>4,000\) | コールブルックの式 $$\frac{1}{\sqrt{\lambda}}=-2\ {\rm log}\left( \frac{\varepsilon}{3.71d} +\frac{2.51}{Re\sqrt{\lambda}}\right)$$ →ムーディ線図で求めるのが一般的 |
先ほども述べた通り、配管設計においてはほとんどの場合で乱流、
かつ粗面管の条件となります。
従ってムーディ線図から管摩擦係数を求める場合が最も多いでしょう。
まとめ
管摩擦係数の計算方法と、ムーディ線図の使い方について解説しました。
ポイントをまとめます。
- 管摩擦係数は「配管内部の表面粗さ」と「流体のレイノルズ数」で決まる
- 最も多い「粗面管かつ乱流」の条件において管摩擦係数はコールブルックの式で与えられる
- コールブルックの式は直接解けないのでムーディ線図で求める事が一般的
- 相対粗さとレイノルズ数を求めれば、ムーディ線図から管摩擦係数を読み取れる
皆様の参考になれば幸いです。








