【曲げ応力とは？】意味・求め方・公式の導出方法を分かりやすく解説│プラントエンジの樹

部材を曲げた時に内部に発生する力を「曲げ応力」と言います。梁などの長い部材では、引張やせん断ではなく曲げ応力で壊れる事が多いため、曲げ応力を正しく求める事が重要です。

本記事では、曲げ応力の意味・求め方・公式の導出方法を分かりやすく解説します。

1 曲げ応力とは
- 1.1 曲げ応力とは何か？
- 1.2 曲げモーメントとの関係
2 曲げ応力の公式
3 曲げ応力の公式の導出
4 まとめ

曲げ応力とは

曲げ応力とは何か？

曲げ応力とは、曲げた部材の内部に発生する引張・圧縮応力のことです。

下図のように部材を曲げた場合、上半分は圧縮方向、下半分は引張方向に応力が掛かります。これらの応力をまとめて曲げ応力と言います。曲げ応力には以下の特徴があります。

凸側は引張、凹側は圧縮となる
中立面から遠いほど大きくなるように分布し、表面で最大となる

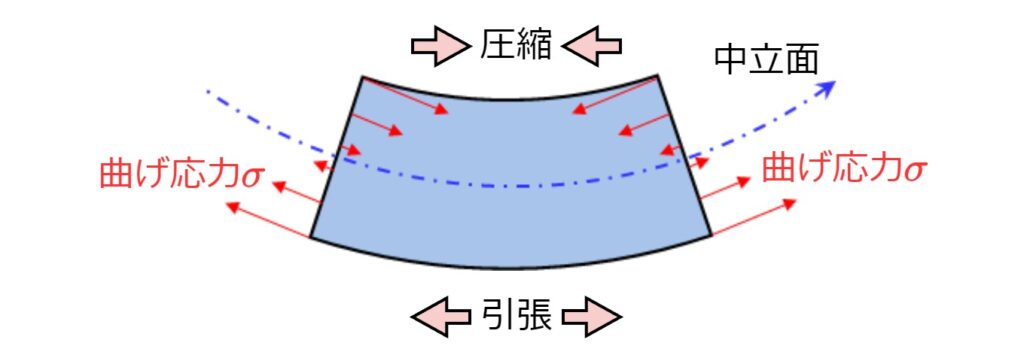
なお、中立面とは引張も圧縮もかからない面のことです。上下対象の断面形状の場合は、断面高さの半分の位置になります。

曲げモーメントとの関係

「曲げ応力」と「曲げモーメント」は名前が似ていますが別物です。

名称	記号	単位	説明
曲げモーメント	$$M$$	$$\rm_{N・m}$$	部材を曲げようとする力（断面を回転させる力）
曲げ応力	$$\sigma$$	$$\rm_{Pa}$$	部材の内部に発生する引張・圧縮応力

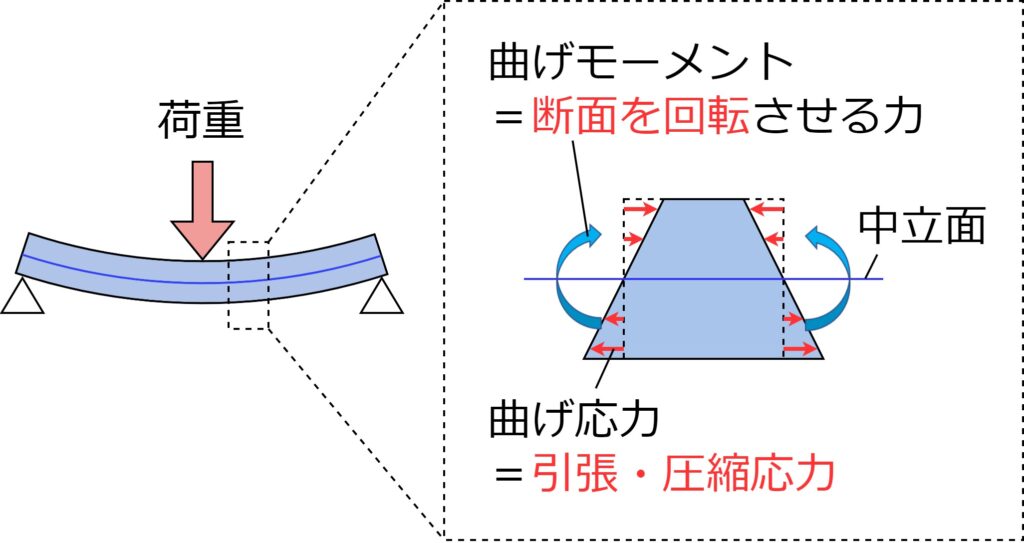
曲げモーメントとは、部材を曲げようとする力そのものです。

少し厳密に言うと、曲げられた部材の内部に発生する「断面を回転させる力（モーメント）」のことです。ある断面に対し、「曲げ応力×中立面からの距離」を足し合わせた物が曲げモーメントと考えることができます。

「曲げ応力」と「曲げモーメント」との違いは、下図のイメージです。

なお、曲げモーメントについては別の記事で詳しく解説しています。

【図解】曲げモーメントとは？計算方法・公式をわかりやすく解説

梁の曲げを考える際には「曲げモーメント」が登場します。言葉の分かりやすさから、理解した気になりやすい曲げモーメント。本記事では、そんな曲げモーメントの考え方・計算方法・公式について一からわかりやすく解説します。 […]

曲げ応力の公式

曲げ応力は以下の公式で求めます。

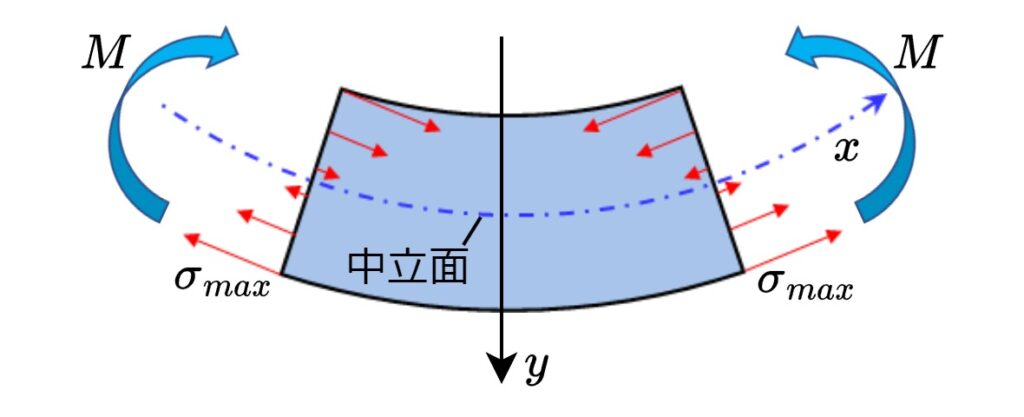
$$\sigma_{max}=\frac{M}{Z}$$

$\sigma_{max}$：曲げ応力の最大値（＝部材の表面における曲げ応力）
$M$：曲げモーメント
$Z$：断面係数

曲げモーメント$M$を断面係数$Z$で割ると、曲げ応力$\sigma_{max}$が求められます。重要な公式ですので覚えましょう。

なお断面係数$Z$とは「どれだけ応力の立ちにくい断面形状か」を表す物理量で、断面形状と寸法が分かれば求められます。詳しくはこちらの記事で解説しています。

曲げ応力を$\sigma_{max}$と最大値で表現しているのは、曲げ応力は中立面から遠いほど大きくなるように分布しており、表面で最大となるからです。従って最大値$\sigma_{max}$を求める上記の公式を最も頻繁に使います。

曲げ応力の公式の導出

上述した曲げ応力の公式$\sigma_{max}=M/Z$の意味と導出方法について解説します。公式を導出する流れを簡単にでも頭にいれておくと、試験などの本番で公式を忘れにくくなります。

引張圧縮の場合は、荷重が与えられたとき、単に断面積で割れば応力を求められますが、曲げの場合は曲げモーメント$M$が与えられても直接応力を求める事ができません。

そこで、以下のステップを踏みます。

曲げ変形の形状を「円弧」と仮定する
曲げ変形によるひずみを、幾何学的に求める
応力とひずみの関係式から、曲げ応力を求める
断面におけるモーメントの釣り合いから、曲げ応力と曲げモーメントの関係を求める

①曲げ変形の形状を「円弧」と仮定する

始めに、梁が曲げられた時の形状を仮定します。

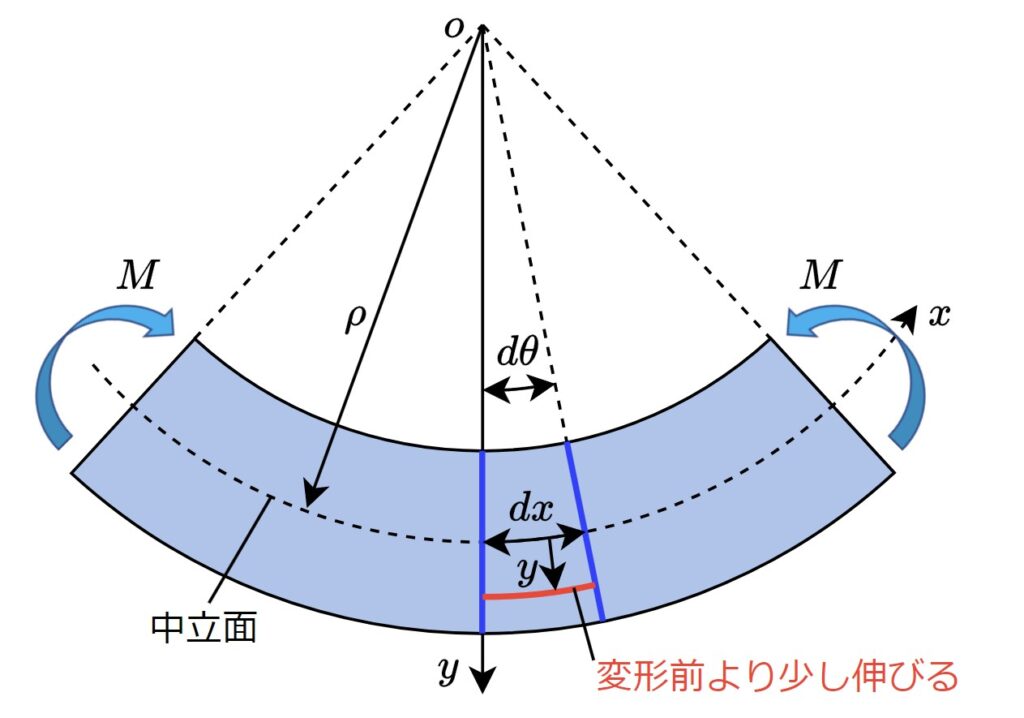
下図のように曲げモーメントを受ける梁を考えます。曲げモーメントは長さに沿って均一に掛かるので、変形もまた、長さに沿って均一に起こると考える事ができます。

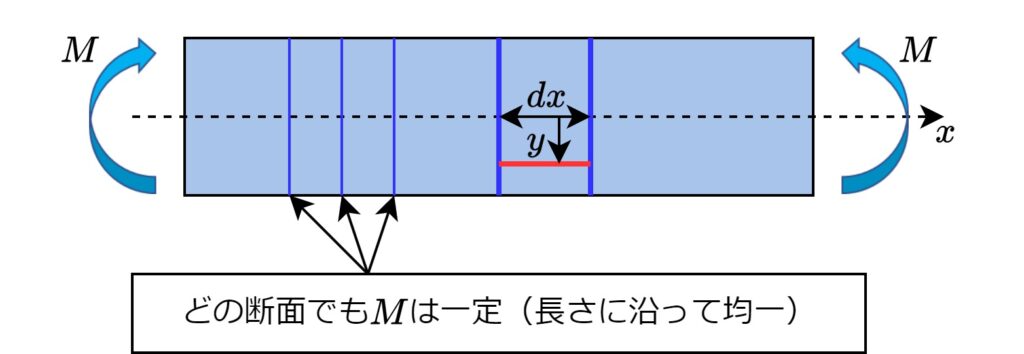
そこで、曲げ変形が下図のように円弧状に起こると仮定します。ここで$\rho$を曲率半径、$x$軸に沿った面を中立面（引張も圧縮も起こらない面）と呼びます。

②曲げ変形によるひずみを、幾何学的に求める

上図において、中立面から下側に距離$y$離れた位置の繊維は、引っ張られて少しだけ伸びている状態になります。この伸び量（ひずみ）を求めます。

中立面における、伸びていない繊維の長さ$dx$は、曲率半径$\rho$と角度$d\theta$から$dx=\rho d\theta$と書けます。これが距離$y$離れた位置では半径が大きくなる分$(\rho＋y)d\theta$となりますから、ひずみ$\varepsilon$は次のようになります。

$$\varepsilon=\frac{(\rho+y)d\theta-dx}{dx}=\frac{yd\theta}{dx}=\frac{y}{\rho}$$

ひずみ$\varepsilon=y/\rho$の関係は後ほど何度か使うので覚えておいてください。

③応力とひずみの関係式から、曲げ応力を求める

フックの法則$\sigma=E\varepsilon$（$E$：ヤング率）より、曲げ応力$\sigma$は以下のように書けます。

$$\sigma=E\varepsilon=\frac{Ey}{\rho}$$

中立面からの距離$y$に比例して曲げ応力$\sigma$が大きくなる、という関係式を求める事ができました。あとは、距離$y$と曲げモーメント$M$の関係を求めれば、$\sigma$と$M$の関係が分かります。

④断面における曲げモーメントの釣り合いから、曲げ応力と曲げモーメントの関係を求める

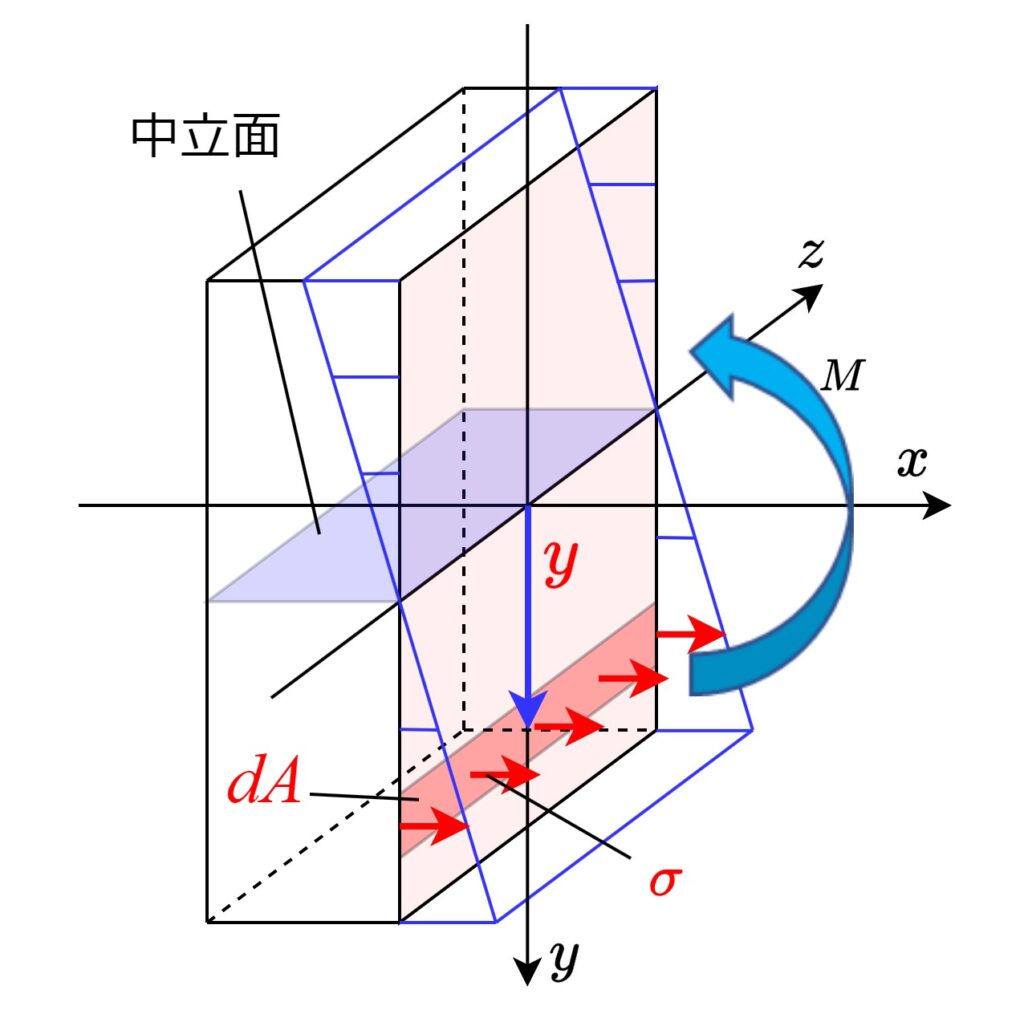
上図のように断面の中の微小断面積$dA$にかかる曲げ応力を$σ$とします。この微小断面にかかる力$\sigma dA$に距離$y$を掛けたモーメントを、断面にわたって足し合わせたものが曲げモーメント$M$ですから、以下のように書けます。

$$M=\int_{A}y\times\sigma dA=\frac{E}{\rho}\int_{A}y^2dA=\frac{EI}{\rho}$$
（ただし、$I=\int_{A}y^2dA$）

$I$を断面二次モーメントと呼びます。断面二次モーメントとは「どれだけ変形しにくい断面形状か」を表す物理量です。詳しくは別の記事で解説しています。

【図解】断面二次モーメントとは？「二次モーメント」の意味と計算式を解説

梁の曲げを考える際には「断面二次モーメント」が登場します。材料力学で習いますが名前からして取っつき難く、公式は知っているが良く分からないモノ、という印象があるかと思います。本記事では断面二次モーメントとは何か、どんな意[…]

また上式を少し変形すると、

$$\frac{1}{\rho}=\frac{M}{EI}$$

となります。この式は曲げた梁の中立面における曲率$1/\rho$は、曲げモーメント$M$に比例し、$EI$（これを曲げ剛性と言います）に反比例することを示した重要な関係式です。本記事では詳細を割愛しますが、梁のたわみを求める際に使います。梁のたわみの求め方についてはこちらの記事、たわみの公式の導出方法についてはこちらの記事でそれぞれ詳しく解説しています。

ステップ③で求めた$\sigma=Ey/\rho$の関係式に、上式を代入します。

$$\sigma=\frac{My}{I}$$

これで曲げモーメント$M$が与えられた時に、中立面から距離$y$の位置における曲げ応力$σ$を求めることが出来ます。

ただ、通常は梁の表面に発生する曲げ応力の最大値$\sigma_{max}$だけが分かれば良い事がほとんどです。もう少し扱いやすいような工夫として、断面係数$Z$を以下のように定義します。

$$Z=\frac{I}{e}$$

$e$は中立面から梁の表面までの距離です。上下対象の断面形状の場合は、梁の高さの半分になります。

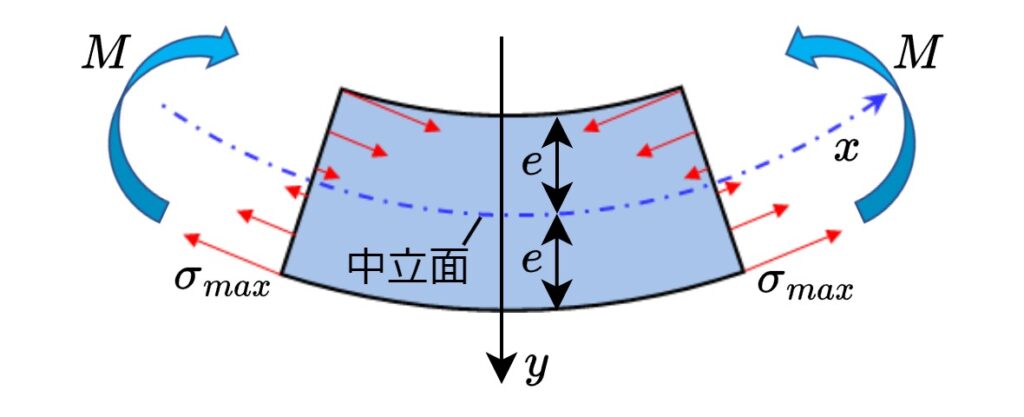
断面係数$Z$を定義したことにより$\sigma=My/I$から$y$を消す事ができ、少しだけシンプルな式になります。つまり、梁の表面$y=e$における曲げ応力$\sigma_{max}$は次のようになります。

$$\sigma_{max}=\frac{M}{Z}$$

$\sigma_{max}$：曲げ応力の最大値（＝梁の表面における曲げ応力）
$M$：曲げモーメント
$Z$：断面係数

以上で曲げ応力の公式が導出されました。
曲げ応力$\sigma_{max}$は曲げモーメント$M$に比例して大きくなり、断面係数$Z$（応力の立ちにくさを表す物理量）に反比例して小さくなる、というイメージし易い結果だと思います。

なお、曲げモーメント$M$については、別の記事で詳しく解説しています↓

【図解】曲げモーメントとは？計算方法・公式をわかりやすく解説

断面係数$Z$についても、別の記事で詳しく解説しています↓

【図解】断面係数とは？初心者でも分かるように意味・求め方を解説

梁の曲げを考える際、「断面係数」という物理量が登場します。本記事では断面係数の意味・求め方を初学者でも分かるよう、図解を交えて詳しく解説します。「断面係数」とは何か？何を表しているのか「断面係数」とはズ[…]

まとめ

曲げ応力の意味・求め方・公式の導出方法について解説しました。

ポイントをまとめます。

曲げ応力とは、曲げた部材の内部に発生する引張・圧縮応力のこと。
曲げ応力は中立面を境に、凸側は引張、凹側は圧縮となる。
曲げ応力は中立面から遠いほど大きく、表面において最大となる。
曲げ応力は以下の公式で求める：$$\sigma_{max}＝\frac{M}{Z}$$
$\sigma_{max}$：曲げ応力の最大値（＝部材の表面における曲げ応力）
$M$：曲げモーメント
$Z$：断面係数