梁に荷重が加わった時の変形量を「たわみ」と言います。
たわみの大きさは公式を使えば簡単に計算する事ができますが、本記事では公式の導出方法・考え方を図解で分かりやすく解説します。
導出の流れを頭に入れておくと、試験で公式を忘れてしまった際も思い出し易くなります。
たわみの公式とは
たわみとは、梁に荷重が加わった時の変形量です。
どれほど頑丈な梁であっても、荷重が加わる以上は常に微小なたわみが発生しています。たわみを求める公式は梁の支持条件や荷重の加わり方によって異なりますが、例えば以下があります。
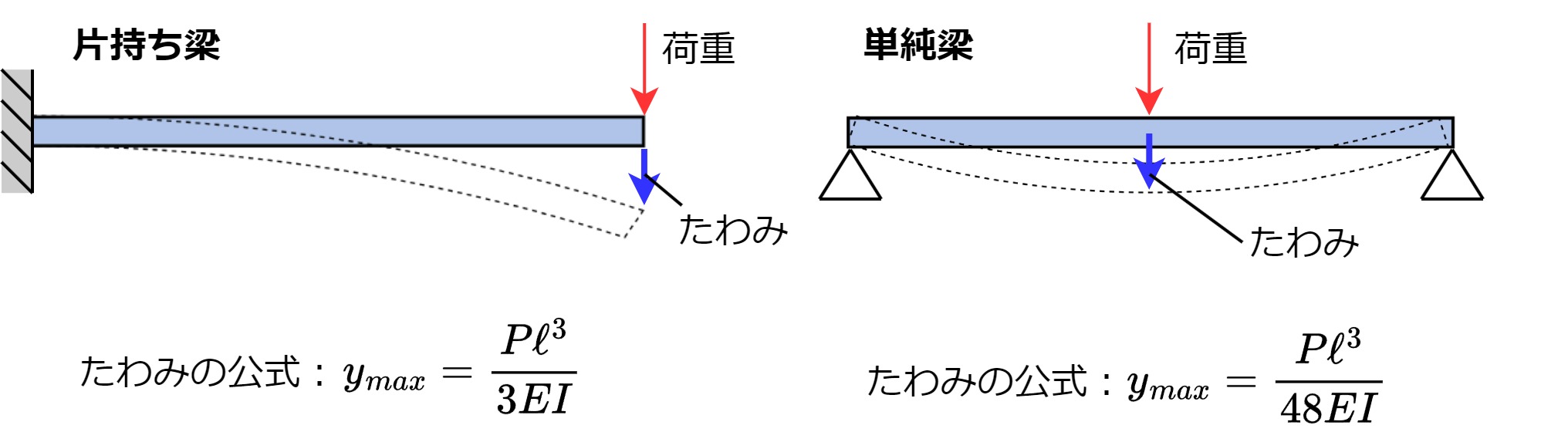
上記以外の様々なパターンにおけるたわみの公式については別の記事でまとめています。実務・試験勉強で役立つような覚え方も紹介していますので参考にしてください。
梁に荷重が加わったとき、梁が変形する量を「たわみ」と言います。 本記事では、材料力学におけるたわみの求め方、試験等で役立つ公式の覚え方をわかりやすく解説します。 たわみとは 「たわみ」とは何か たわみとは、梁に[…]
たわみの公式の導出方法
たわみの公式の導出方法について解説します。
公式の導出は、大まかに以下の手順で行います。
- 幾何学的な関係から、たわみ曲線の微分方程式を導出する
- 微分方程式から、たわみ曲線の式を求める
- たわみ曲線の式から、たわみの最大値（たわみの公式）を求める
①は材料力学の理解を深めるために知っておきたいという程度ですが、②以降は試験で公式を忘れてしまった際にも非常に役立ちますので、是非覚えておきたい内容です。
① 幾何学的な関係から、たわみ曲線の微分方程式を導出する
梁の変形状態を式で表すために、まず下図のようにモデル化します。
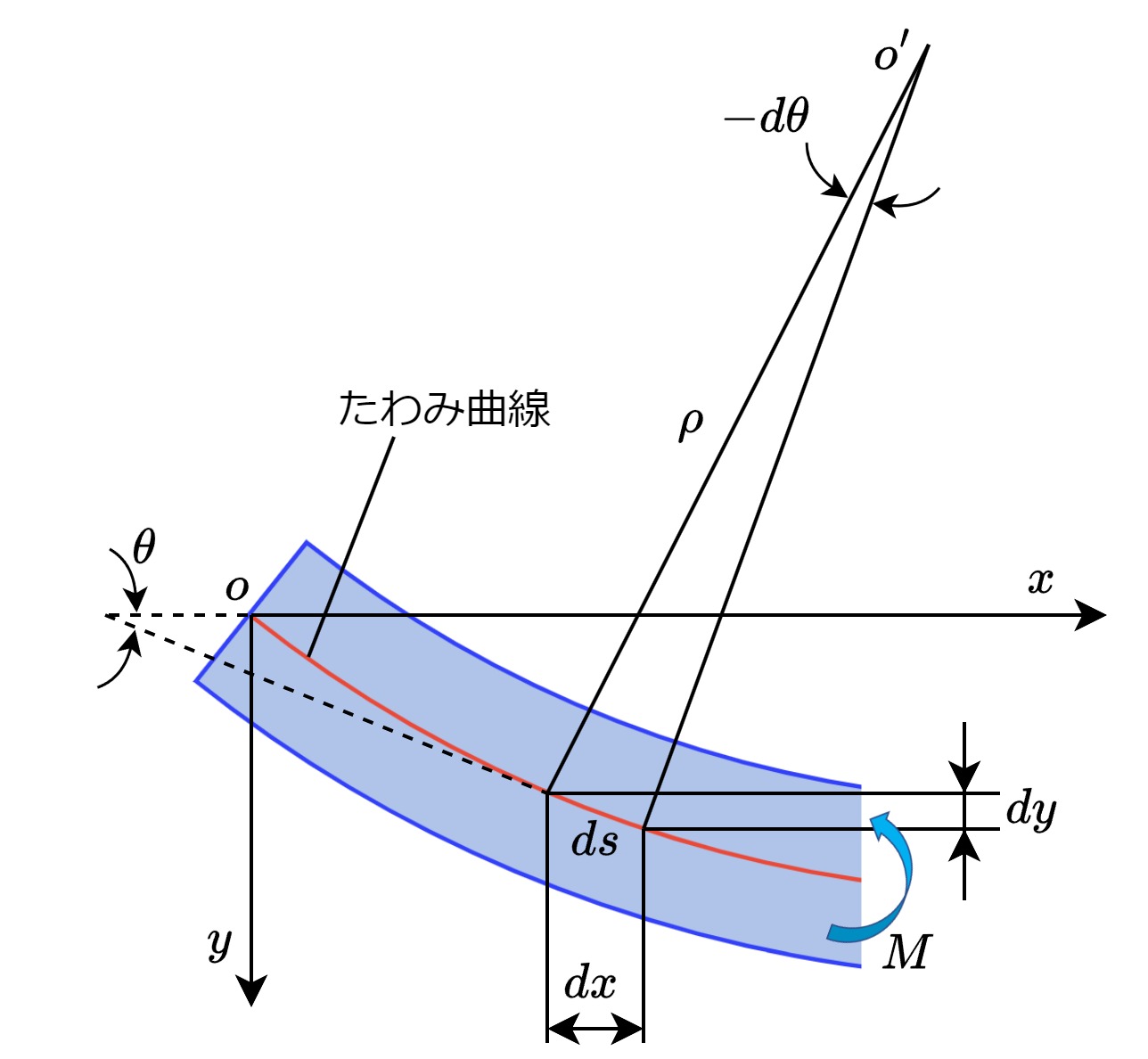
- たわみ曲線：梁の中心軸を表す曲線。この曲線で変形を代表する。
- たわみ角\(\theta\)：たわみ曲線と変形前の軸線とのなす角
- たわみ\(y\)：垂直方向の変位
- 位置\(x\)：軸方向の位置
上図から読み取れる3つの幾何学的な関係式から、「たわみ曲線の微分方程式」を導出する事ができます。導出過程を分かり易くするため、式展開や導入の流れを下に図示します。
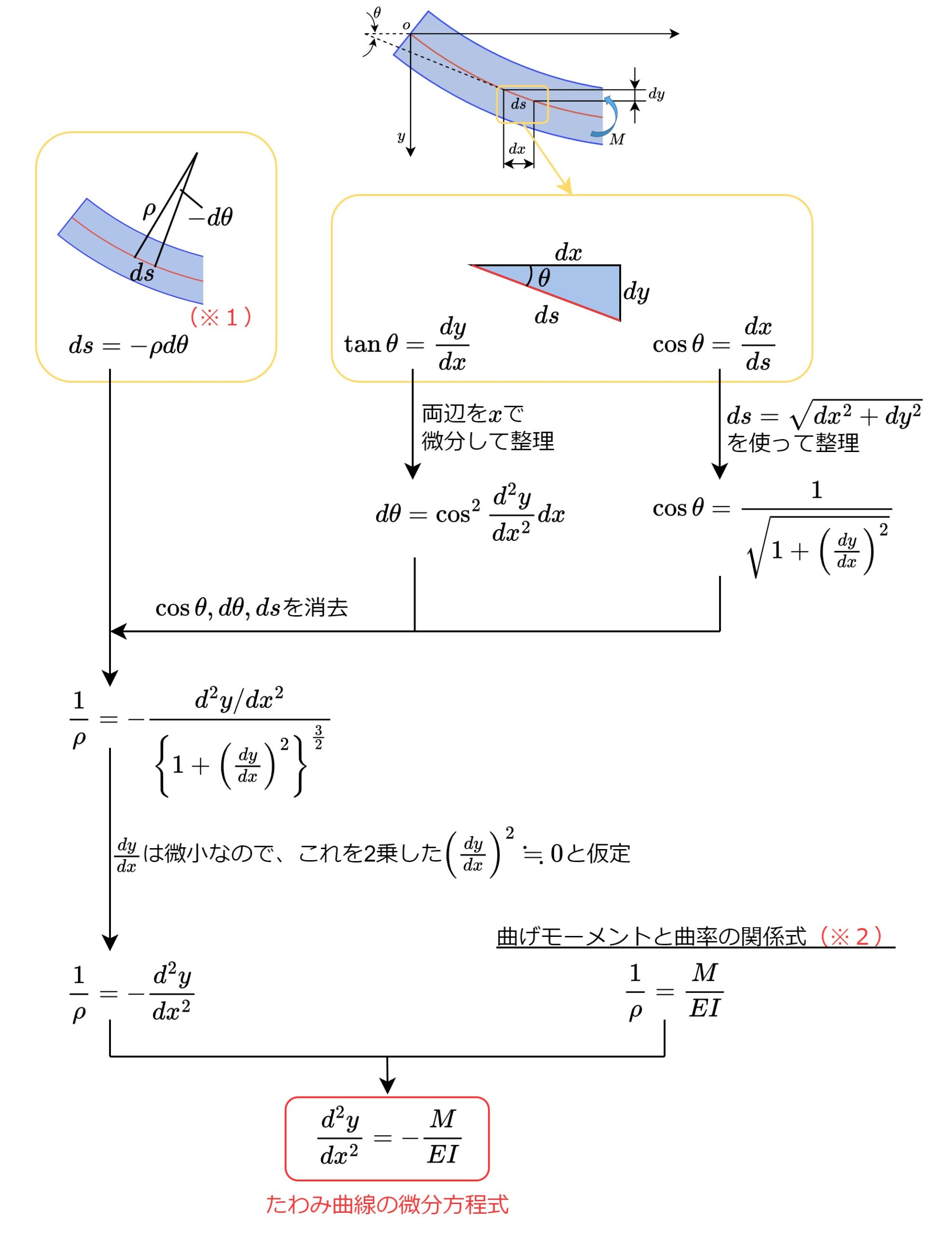
※１：たわみ角\(\theta\)は\(x\)が右に行くに従って小さくなるので、\(-d\theta\)と負の値で表現します。
※２： 曲げモーメント\(M\)と曲率\(1/\rho\)の関係式です。詳しくはこちらの記事（【曲げ応力とは？】意味・求め方・公式の導出方法を分かりやすく解説）で解説しています。
上の式展開で導出された式が、「たわみ曲線の微分方程式」です。
$$\frac{d^2y}{dx^2}=-\frac{M}{EI}$$
- \(M\)：曲げモーメント
- \(E\)：ヤング率
- \(I\)：断面二次モーメント
この微分方程式1つをを暗記しておけば、全てのたわみの公式を求める事ができます。
なお、たわみ角\(\theta\)は微小と考えて、
$$\theta=\frac{dy}{dx}$$
と表します。従って、たわみ曲線の微分方程式を1度積分するとたわみ角\(\theta\)が求まり、もう一度積分するとたわみ\(y\)が求まります。
② 微分方程式から、たわみ曲線の式を求める
たわみ曲線の微分方程式から、以下のStepでたわみ曲線の式を求めます。
- 1) 曲げモーメント\(M\)を\(x\)の関数で表す
- 2) 微分方程式に\(M\)を代入して二階積分する
- 3) 梁の支持条件から積分定数を求める
例として「先端に集中荷重の掛かる片持ち梁」のたわみ曲線の式を導出していきます。
1) 曲げモーメント\(M\)を\(x\)の関数で表す
たわみ曲線の微分方程式
$$\frac{d^2y}{dx^2}=-\frac{M}{EI}$$
において、\(x\)の関数となる（積分される）のは通常は曲げモーメント\(M\)のみですので、まずは\(M\)を\(x\)の関数で表します。（梁の断面形状が位置\(x\)によって変化するような梁の場合は、\(EI\)も\(x\)の関数となりますが、このような問題を扱う事は稀です。）
下図のような片持ち梁では、曲げモーメント\(M\)は次のように表されます。
$$M=-P \left( \ell-x \right)$$
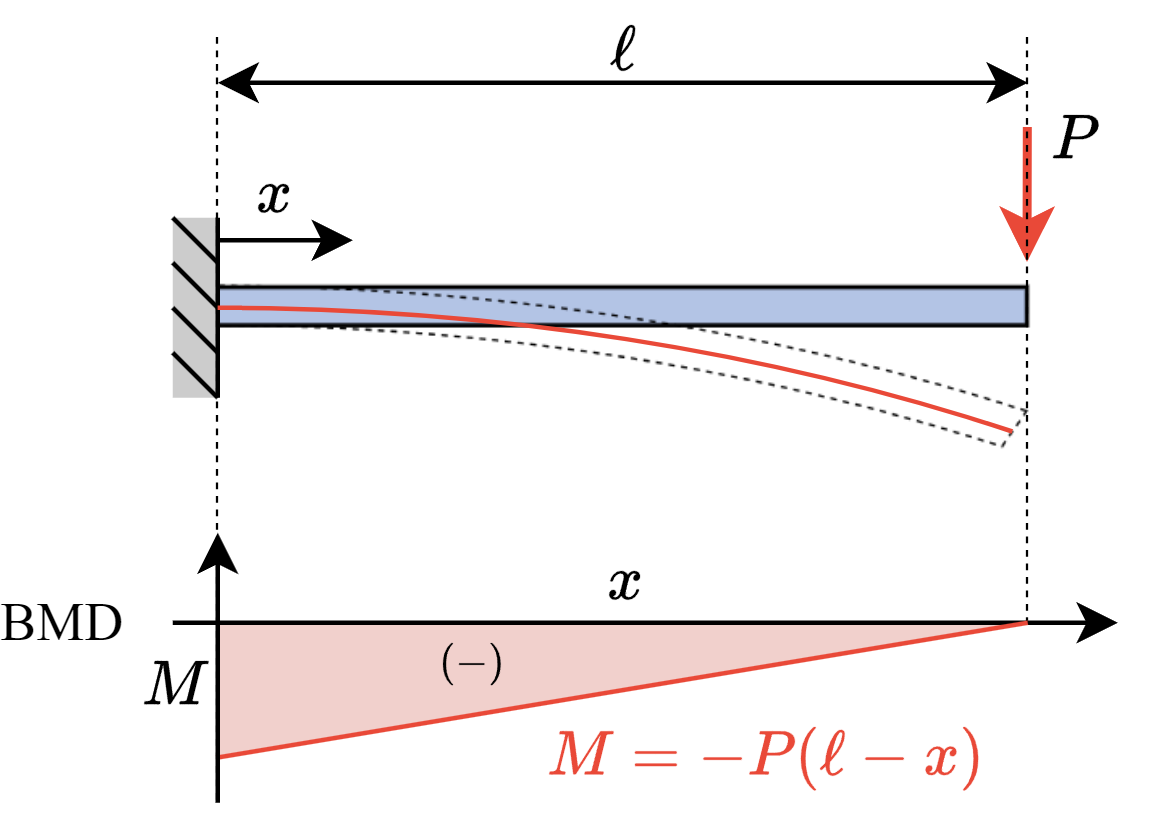
なお、曲げモーメント\(M\)の求め方については、以下の記事で詳しく解説しています。
梁の曲げを考える際には「曲げモーメント」が登場します。 言葉の分かりやすさから、理解した気になりやすい曲げモーメント。 本記事では、そんな曲げモーメントの考え方・計算方法・公式について一からわかりやすく解説します。 […]
梁の曲げ問題ではせん断力と曲げモーメントを求め、その分布をグラフにした「せん断力図」と「曲げモーメント図」を作成します。 本記事では、せん断力図と曲げモーメント図の描き方と、試験等でも役立つ「覚えておくべきグラフの特徴5つ」を解説し[…]
2) 微分方程式に\(M\)を代入して二階積分する
上で求めた曲げモーメント\(M\)の式をたわみ曲線の微分方程式に代入します。
$$\frac{d^2y}{dx^2}=-\frac{M}{EI}=\frac{P}{EI}(\ell-x)$$
これを積分していくと次のようになります。
$$\frac{dy}{dx}=\theta=\frac{P}{EI}\left( \ell x-\frac{1}{2}x^2+C_1\right) \tag{A}$$
$$y=\frac{P}{EI}\left( \frac{1}{2}\ell x^2-\frac{1}{6}x^3+C_1x+C_2 \right) \tag{B}$$
式\((\rm{A})\)は梁のたわみ角\(\theta\)（\(=dy/dx\)）の式、式\((\rm{B})\)は梁のたわみ\(y\)の式（＝たわみ曲線の式）です。あとは積分定数\(C_1,C_2\)が分かれば、たわみ曲線の式が求められます。
3) 梁の支持条件から積分定数を求める
数学ではお馴染みの「境界条件を与えて積分定数を求める」という作業を行います。
難しい話ではなく、「梁の根本\(x=0\)の位置ではたわみ\(y=0\)となるはず」といった当たり前の条件から\(C_1,C_2\)を求めるだけの作業です。境界条件は、求めたい積分定数と同じ数だけ必要です。今回は積分定数が\(C_1,C_2\)と2つあるので、以下の2つの境界条件を考えます。
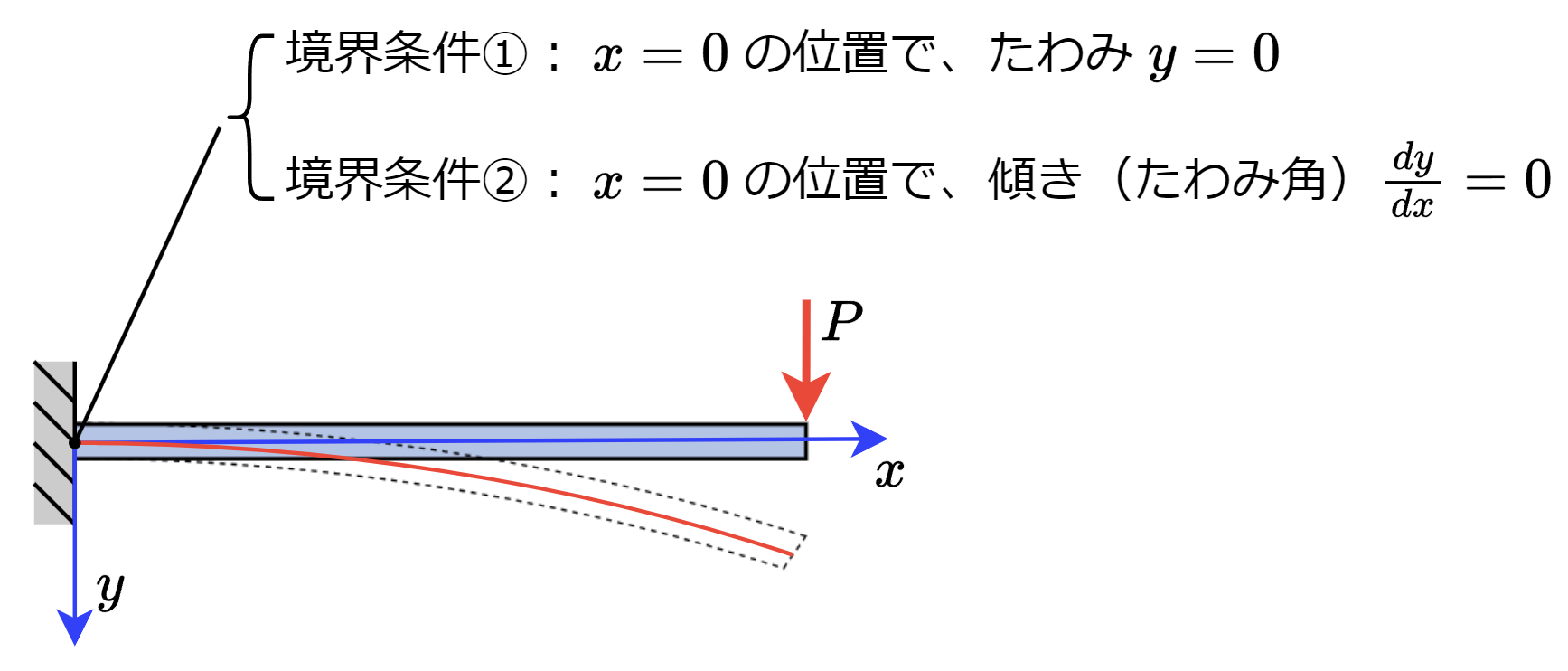
片持ち梁以外でも、境界条件は梁の固定点におけるたわみ\(y\)や、たわみ角\(dy/dx\)の条件から簡単に決められます。
さて境界条件①②を式\((\rm{A})\),\((\rm{B})\)に代入すると、シンプルに\(C_1=0,C_2=0\)と計算できます。従ってたわみ\(y\)の式は次のようになります。
$$y=\frac{P}{EI}\left( \frac{1}{2}\ell x^2-\frac{1}{6}x^3 \right)$$
これでたわみ曲線の式を求める事ができました。
③ たわみ曲線の式から、たわみの最大値（たわみの公式）を求める
たわみ曲線の式に、たわみが最大となる位置\(x\)を代入すればたわみの公式が導出できます。
どの位置でたわみが最大となるかは、支持条件をイメージして考えるのが手っ取り早いです。（もちろん、たわみ曲線の式をグラフに書いて確認する方法もあります）
片持ち梁の場合、梁の先端でたわみが最大となる事は感覚的に分かると思います。
よってたわみ曲線の式に\(x=\ell\)を代入した
$$y=\frac{P\ell^3}{3EI}$$
が、先端に集中荷重が掛かる片持ち梁における、たわみの最大値を求める公式となります。
以上が公式の導出方法です。長い手順に感じるかもしれませんが、Step②③の流れだけでも理解しておくと、たわみの公式を忘れてしまった際に自分で導出できます。
まとめ
たわみの公式の導出方法
たわみの公式の導出方法を解説しました。
導出の流れをまとめます。
- 幾何学的な関係から、たわみ曲線の微分方程式を導出する
（微分方程式は丸暗記でも可）
$$\frac{d^2y}{dx^2}=-\frac{M}{EI}$$ - 微分方程式から、たわみ曲線の式を求める
1) 曲げモーメント\(M\)を\(x\)の関数で表す
2) 微分方程式に\(M\)を代入して二階積分する
3) 梁の支持条件から積分定数を求める - たわみ曲線の式に、たわみが最大となる位置xを代入し、最大値（たわみの公式）を求める
参考文献
本記事の解説は下記の書籍を参考にしています。図解が多く、材料力学を勉強するには最適な教科書だと思います。運営者も購入して10年以上経ちますが、いまだに仕事や資格勉強で使うのでオススメです。
