梁に荷重が加わったとき、梁が変形する量を「たわみ」と言います。
本記事では、材料力学におけるたわみの求め方、試験等で役立つ公式の覚え方をわかりやすく解説します。
たわみとは
「たわみ」とは何か
たわみとは、梁に荷重が加わった時の変形量です。
どれほど頑丈な梁であっても、荷重が加わる以上は常に微小なたわみが発生しています。
基本的に、たわみは可能な限り小さくなるよう設計されます。
建築業界においては、たわみ量は梁の長さの1/250以下に抑える等の基準が定められています。
（参考資料：建築構造設計基準の資料- 国土交通省）
たわみの大きさを決める要素
たわみの大きさ（たわみ量）は以下の５つの条件によって決まります。
- 梁の支持条件：
片持ち梁、単純梁といった梁の支持条件によって、使う公式が異なります。 - 荷重条件：
集中荷重、分布荷重といった荷重条件によっても、使う公式が異なります。 - 荷重の大きさ：
当然ですが、荷重が大きいほどたわみは大きくなります。 - 梁の長さ：
梁が長いほど、たわみは大きくなります。梁が長いと小さなたわみが積み重なり、結果として大きなわたみとなるイメージです。 - 曲げ剛性\(EI\)（\(E\)：ヤング率、\(I\)：断面二次モーメント）：
曲げ剛性（=\(E\times I\)）が大きいほどたわみは小さくなります。
・ヤング率\(E\)：材料の物性値で、引っ張った際の伸びにくさを表します。
・断面二次モーメント\(I\)：梁の断面形状から算出できる数値で、曲げた際の変形し難さを表します。
断面二次モーメント\(I\)の考え方と計算方法は、梁のたわみを求める際には必ず理解しておきたいものです。詳細は以下の記事で解説しています。
梁の曲げを考える際には「断面二次モーメント」が登場します。 材料力学で習いますが名前からして取っつき難く、公式は知っているが良く分からないモノ、という印象があるかと思います。 本記事では断面二次モーメントとは何か、どんな意[…]
たわみを求める公式一覧
種々の支持条件における、たわみの最大値を求める公式を示します。
記号は以下を使用します。
- \(y_{max}\)：たわみの最大値
- \(P\)：荷重
- \(q\)：単位長さあたりの荷重（分布荷重）
- \(\ell\)：梁の長さ
- \(E\)：ヤング率
- \(I\)：断面二次モーメント
| 支持条件・荷重条件 | 梁の状態 | たわみの最大値の公式 |
|---|---|---|
| 片持ち梁・集中荷重 | 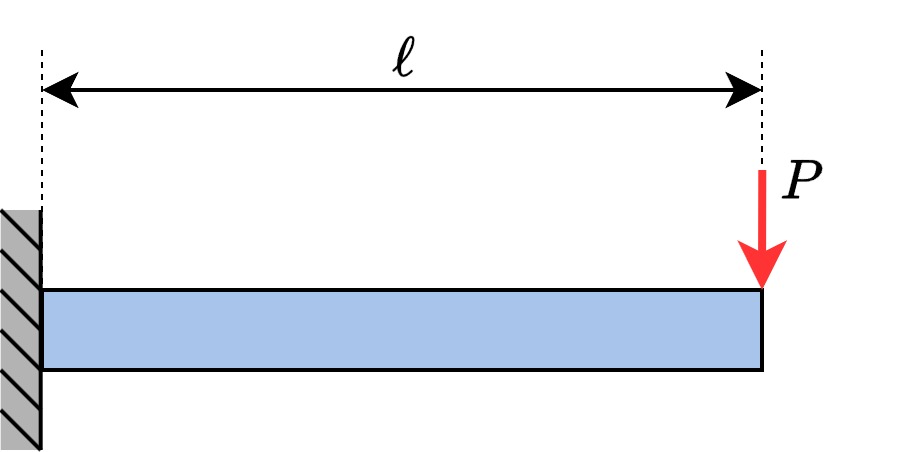 | $$y_{max}=\frac{P\ell^3}{3EI}$$ |
| 片持ち梁・等分布荷重 | 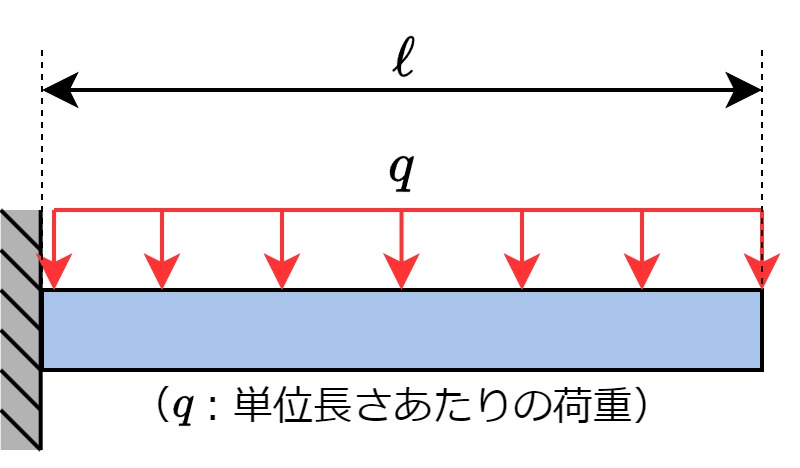 | $$y_{max}=\frac{q\ell^4}{8EI}$$ |
| 単純梁・集中荷重 | 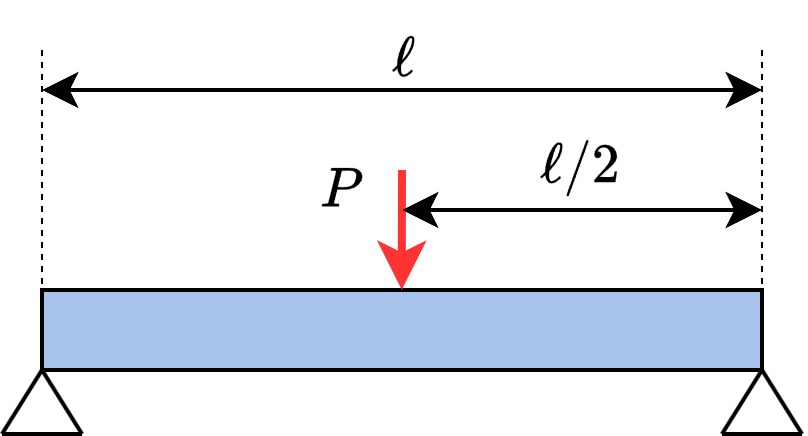 | $$y_{max}=\frac{P\ell^3}{48EI}$$ |
| 単純梁・等分布荷重 | 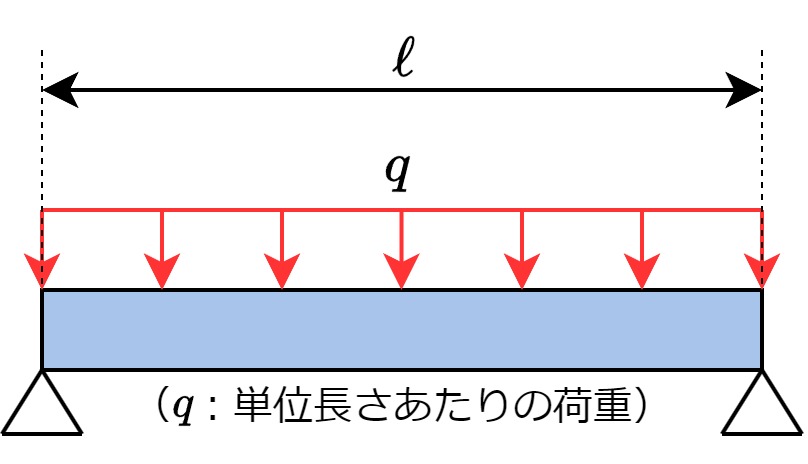 | $$y_{max}=\frac{5q\ell^4}{384EI}$$ |
| 両端固定梁・集中荷重 | 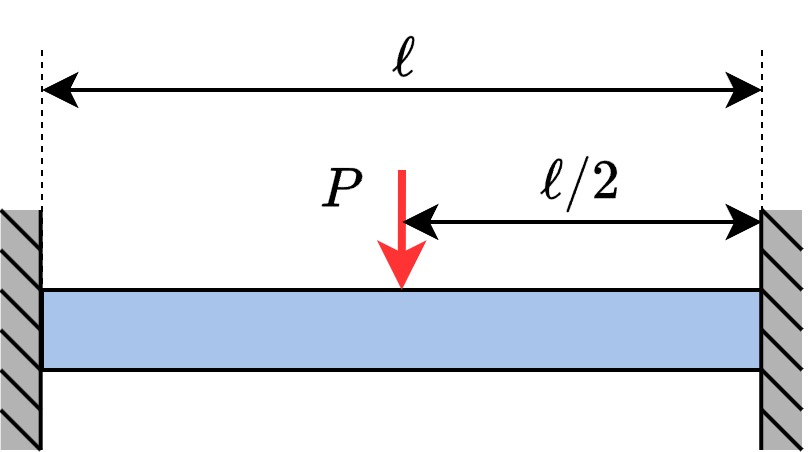 | $$y_{max}=\frac{P\ell^3}{192EI}$$ |
| 両端固定梁・等分布荷重 | 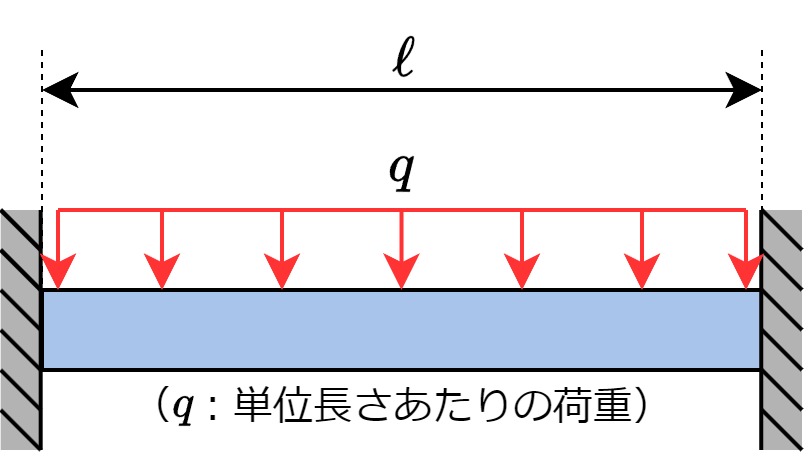 | $$y_{max}=\frac{q\ell^4}{384EI}$$ |
特に、先端に集中荷重の掛かる片持ち梁のたわみの公式：
$$y_{max}=\frac{P\ell^3}{3EI}$$
は最も形がシンプルで覚えやすく、使用頻度も高いので、丸暗記しておくとよいです。
公式の覚え方
たわみの公式を覚えておくと試験などで大変役立ちますが、似た公式が並んでいて、簡単には覚えにくいと思います。以下に覚えるコツを紹介します。
- 記号の配置や次数は、単位換算を考えながら覚える
- 「たわみ易い順」を考えて係数を覚える
- 公式の導出方法を理解する
記号の配置や次数は、単位換算を考えながら覚える
公式の形には以下の法則があります。
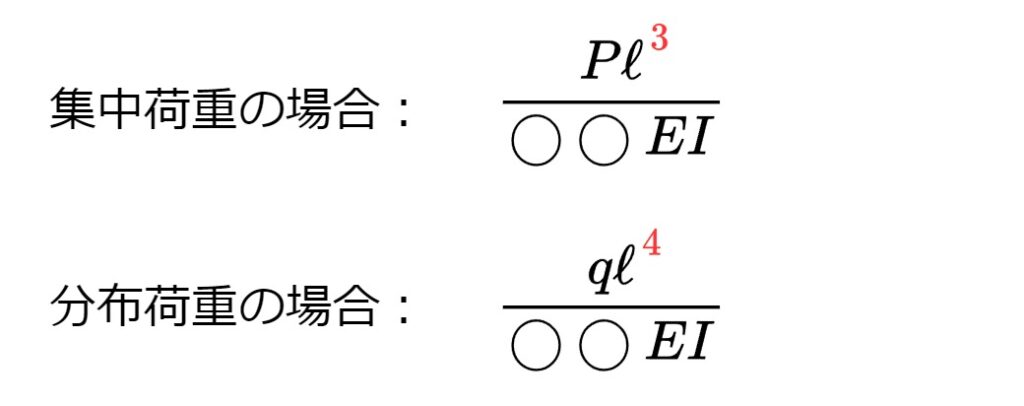
これら記号の配置・次数は単位換算を考えると覚えやすくなります。
一般にたわみの単位は\(\rm{mm}\)を使いますが、単位換算をし易くするため、ここでは単に長さの次元と考えて\(\rm{m}\)とします。同様に公式で使う各記号の単位を考えると以下のようになります。
- 荷重\(P\)：\(\rm{N}\)
- 単位長さあたりの荷重\(q\)：\(\rm{N/m}\)
- ヤング率\(E\)：\(\rm{N/m^2}\)
- 断面二次モーメント\(I\)：\(\rm{m^4}\)
これらを公式に当てはめると、確かにたわみの単位は\(\rm{m}\)となっています。
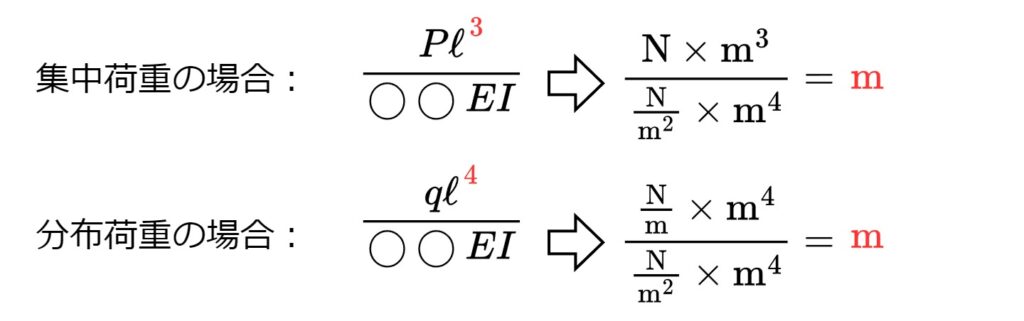
「\(I\)が分母に来るか分子に来るか分からなくなった」「\(\ell\)が3乗か4乗か分からなくなった」といった場合には、このように単位換算により確認できます。
「たわみ易い順」を考えて係数を覚える
記号の前に付く係数「1/〇〇」の覚え方としては、語呂合わせも考えられますが、語呂合わせをいくつも覚えるのも大変です。覚えるボリュームが少しだけ減る別の方法が「たわみ易い順」を考える事です。
片持ち梁＞単純梁＞両端固定梁 の順でたわみは大きくなる
梁の支持条件にはたわみ易い順番があります。以下のように考えると覚えやすいです。
| 片持ち梁 | 根本しか支えられていないので先端の荷重に弱く、最もたわみ易い |
| 単純梁 | 両端が「置いてあるだけ」の状態。片持ち梁と両端固定梁の間のたわみ易さ |
| 両端固定梁 | 両側がしっかり固定されているので最もたわみ難い |
集中荷重＞分布荷重 の順でたわみは大きくなる
例えば同じ10Nを梁に掛けるとき、梁全体に分布させるより、先端や中央に集中させた方がたわみが大きくなる、という事は想像がつきやすいと思います。
これらを踏まえて公式一覧を見ると、確かに「片持ち梁＞単純梁＞両端固定梁」 かつ「集中荷重＞分布荷重」の順に係数が並んでいる事が分かります。
※厳密に言うとこの考え方では、例えば「片持ち梁の分布荷重の係数」＞「単純梁の集中荷重の係数」となる理由は説明できませんが、たまたまこのような順になっているので、覚え方の一つとして参考にしてください。
たわみ易い順の考えを理解したところで、係数の具体手的な覚え方です。分母の数字を揃えた状態で覚えると少しだけ暗記ボリュームが減ります。下の表のように、分母を全て384に揃えて、分子だけ上から順に覚えると良いです。
| 支持条件・荷重条件 （たわみ易い順に並べる） | たわみの最大値の公式 （分母を384に揃えた場合） | 分子 （これを上から順に覚える） |
|---|---|---|
| 片持ち梁・集中荷重 | $$y_{max}=\frac{128P\ell^3}{384EI}$$ | 128 |
| 片持ち梁・等分布荷重 | $$y_{max}=\frac{48q\ell^4}{384EI}$$ | 48 |
| 単純梁・集中荷重 | $$y_{max}=\frac{8P\ell^3}{384EI}$$ | 8 |
| 単純梁・等分布荷重 | $$y_{max}=\frac{5q\ell^4}{384EI}$$ | 5 |
| 両端固定梁・集中荷重 | $$y_{max}=\frac{2P\ell^3}{384EI}$$ | 2 |
| 両端固定梁・等分布荷重 | $$y_{max}=\frac{q\ell^4}{384EI}$$ | 1 |
係数の語呂合わせをいくつも覚えるよりも、少しだけ楽な覚え方を紹介しました。
公式の導出方法を理解する
公式を丸暗記するだけでなく、導出の基本的な考え方を理解する事も重要です。試験で公式を忘れてしまった際に自分で計算できますし、複雑な条件での応用も効きます。
たわみの公式は全て、以下に示す微分方程式を解いたものです。
$$\frac{d^2y}{dx^2}=-\frac{M}{EI}$$
- \(y\)：たわみ
- \(x\)：梁の長さ方向の位置
- \(M\)：曲げモーメント
- \(E\)：ヤング率
- \(I\)：断面二次モーメント
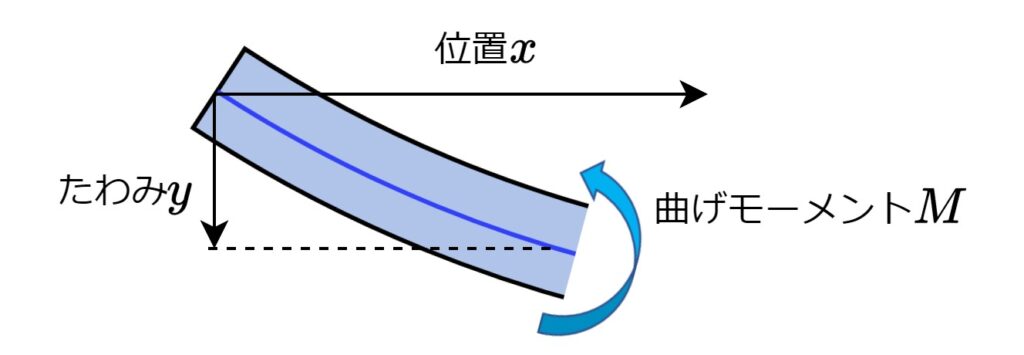
この微分方程式を、各々の支持条件での境界条件を与えながら解くと、全ての公式が導出されます。境界条件というのは「支持点x=0の位置ではたわまないので、y=0」といった条件です。それほど難しい計算でもないので、公式を忘れてしまった時は自分で導出するのも手です。
導出方法の詳細や具体例については、以下の記事で詳しく解説しています。
梁に荷重が加わった時の変形量を「たわみ」と言います。たわみの大きさは公式を使えば簡単に計算する事ができますが、本記事では公式の導出方法・考え方を図解で分かりやすく解説します。 導出の流れを頭に入れておくと、試験で公式を忘れてしまった[…]
まとめ
たわみの求め方・公式の覚え方
材料力学におけるたわみの求め方、試験等で役立つ公式の覚え方を解説しました。
ポイントをまとめます。
- たわみとは、梁に荷重が加わった際の変形量のこと
- たわみは支持条件、荷重条件、荷重の大きさ、梁の長さ、曲げ剛性によって決まる
- 片持ち梁（先端に集中荷重が掛かる場合）のたわみの公式だけでも覚えておくと便利：
$$y_{max}=\frac{P\ell^3}{3EI}$$ - 公式の覚え方：「記号の配置や次数は、単位換算を考えながら覚える」「たわみ易い順を考えて係数を覚える」「公式の導出方法を理解する」
皆様の参考になれば幸いです。
参考文献
本記事の解説は下記の書籍を参考にしています。図解が多く、材料力学を勉強するには最適な教科書だと思います。運営者も購入して10年以上経ちますが、いまだに仕事や資格勉強で使うのでオススメです。
