材料力学では「断面二次モーメント」と「断面係数」が頻出しますが、
名前も算出方法も似ているので混同し易いかと思います。
本記事では断面二次モーメントと断面係数の違いを分かり易く解説します。
断面二次モーメントと断面係数の違い
先に結論を書くと、断面二次モーメントと断面係数の違いはズバリ下の通りです。
| 断面二次モーメント \(I\) | 断面係数 \(Z\) | |
|---|---|---|
| 意味合い | 曲げた時の変形しにくさ(硬さ) | 曲げた時の応力の立ちにくさ(強さ) |
| 使う場面 | はりのたわみ・変形量を求める | はりに掛かる応力を求める |
どちらも断面形状のみによって決まる物理量で、材質などは関係しません。
使う時に便利なように式のまとめ方(定義)が少し違うだけです。
たわみと応力のどちらを求めたいかによって、
断面二次モーメントと断面係数を使い分けます。
ここからは断面二次モーメントと断面係数それぞれについて、
もう少し詳しく解説します。
断面二次モーメントとは
意味合い
曲げた時の変形しにくさ(硬さ)を表す物理量です。
はりのたわみ・変形量を求める際に使います。
断面二次モーメントが大きいほどたわみが小さく、
変形しにくい断面形状である事を意味します。
よく使う公式
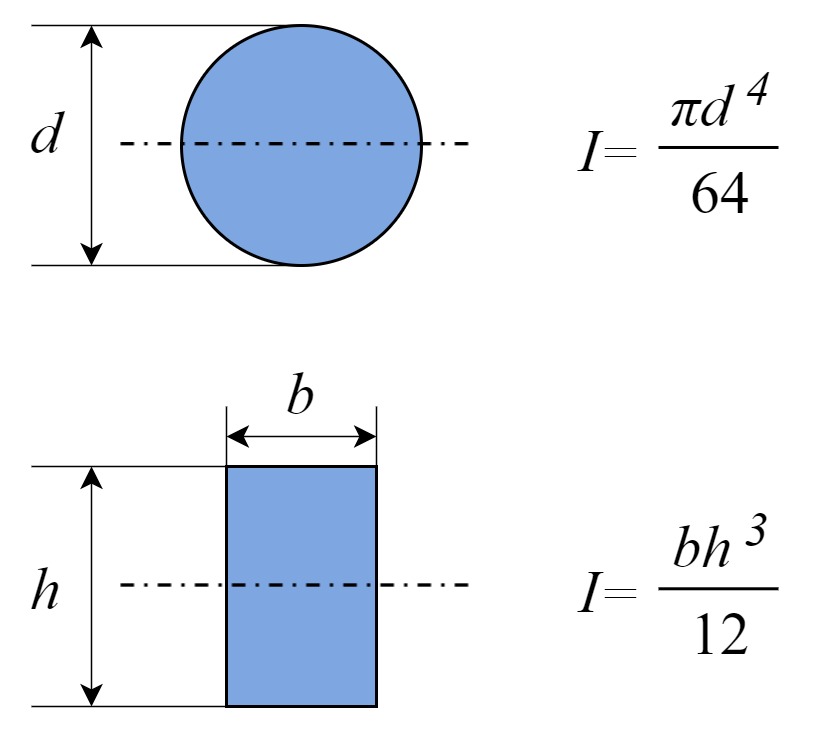
よく使うのは断面形状が円形の時と長方形の時です。
それぞれの断面二次モーメントの公式を記載します。
断面二次モーメントを使う場面
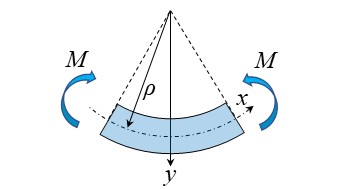
下の図のように断面二次モーメント\(I\)、ヤング率\(E\)のはりに
曲げモーメント\(M\)を掛けたとき、はりの中立面における曲率\(1/ρ\)は
次のように表されます。
\( \frac{1}{\rho}=\frac{M}{EI} \)
この関係式を基として、微分方程式を使いながら式変形していくと、
各条件のはりのたわみ量を計算する事ができます。(詳細は省きます)
例えば下の図のように、長さ\(\ell\)の片持ちはりの先端に集中荷重\(P\)が掛かる場合、
先端のたわみ\(y\)は次のようになります。

\(y=\frac{P\ell^3}{3EI}\)
断面二次モーメント\(I\)が大きいほど、たわみ\(y\)が小さくなる関係になっています。
はりの固定方法や荷重の掛かり方の条件(境界条件)が変われば
細かい係数は変わりますが、たわみ\(y\)が断面二次モーメント\(I\)に反比例する、
というのは変わりません。
「断面二次モーメント\(I\)は、はりのたわみを求める際に使う」
という事がお分かり頂けましたでしょうか。
断面二次モーメントの計算方法・考え方については以下の記事でより詳しく解説しています。
梁の曲げを考える際には「断面二次モーメント」が登場します。 材料力学で習いますが名前からして取っつき難く、公式は知っているが良く分からないモノ、という印象があるかと思います。 本記事では断面二次モーメントとは何か、どんな意[…]
はりのたわみの求め方・公式の覚え方については、以下の記事で詳しく解説しています。
梁に荷重が加わったとき、梁が変形する量を「たわみ」と言います。 本記事では、材料力学におけるたわみの求め方、試験等で役立つ公式の覚え方をわかりやすく解説します。 たわみとは 「たわみ」とは何か たわみとは、梁に[…]
(おまけ)なぜこんな変な名前なのか?
この項はおまけなので、読み飛ばしてOKです。
「断面二次モーメント」という取っ付きにくい名前はどこから来たのか?について、
解説したいと思います。
まずモーメントとは「定点から任意の点までの位置ベクトルと、その点におけるベクトル量の積」と定義されています。
(参考:weblio辞書、 Wikipedia)
要するに「中心までの距離×何か」で表される物理量と解釈できます。
確かに力のモーメントや慣性モーメントも
中心までの距離に力を掛けたり、質量を掛けて表されていますね。
では断面二次モーメントはどうか?について説明するために、
断面二次モーメントの定義を説明します。
下の図のように、曲げが掛かるはりの微小断面を考えたとき、
断面二次モーメント\(I\)は次のように定義されています。
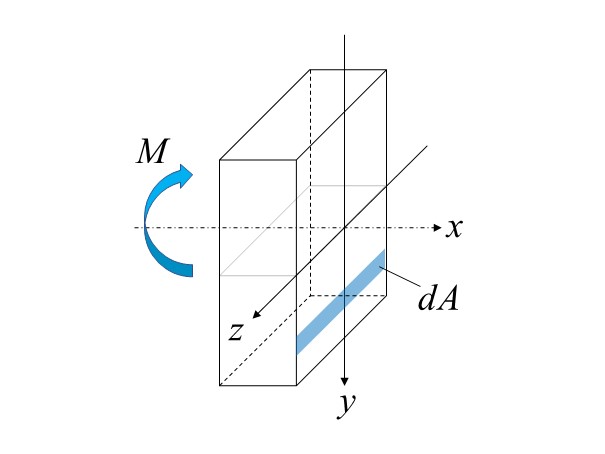
\(I=\int_{A}^{}y^2dA\)
式の意味までは考えなくて良いですが、
中立軸(\(z\)軸)からの距離\(y\)の2乗と微小要素面積\(dA\)を掛けたものの総和
で表されています。
モーメントの定義である「中心までの距離×何か」で表されている上、
\(y\)の2乗(2次)で計算されているので、
「微小断面における2次のモーメント」→「断面二次モーメント」
と名前が決められたのです。
断面係数とは
意味合い
曲げた時の応力の立ちにくさ(強さ)を表す物理量です。
はりに掛かる応力を求める際に使います。
断面係数が大きいほど応力が小さく、
破壊しにくい断面形状である事を意味します。
断面係数\(Z\)は断面二次モーメント\(I\)を使って次のように定義されます。
$$Z=\frac{I}{e}$$
ここで\(e\)は中立軸から表面までの距離です。
断面二次モーメント\(I\)を\(e\)で割っただけですが、
応力を計算する際は\(I\)を使うより\(Z\)を使う方が式の形がシンプルなので、
別の文字を使うというだけです。
よく使う公式
よく使うのは断面形状が円形の時と長方形の時です。
それぞれの断面係数の公式を記載します。
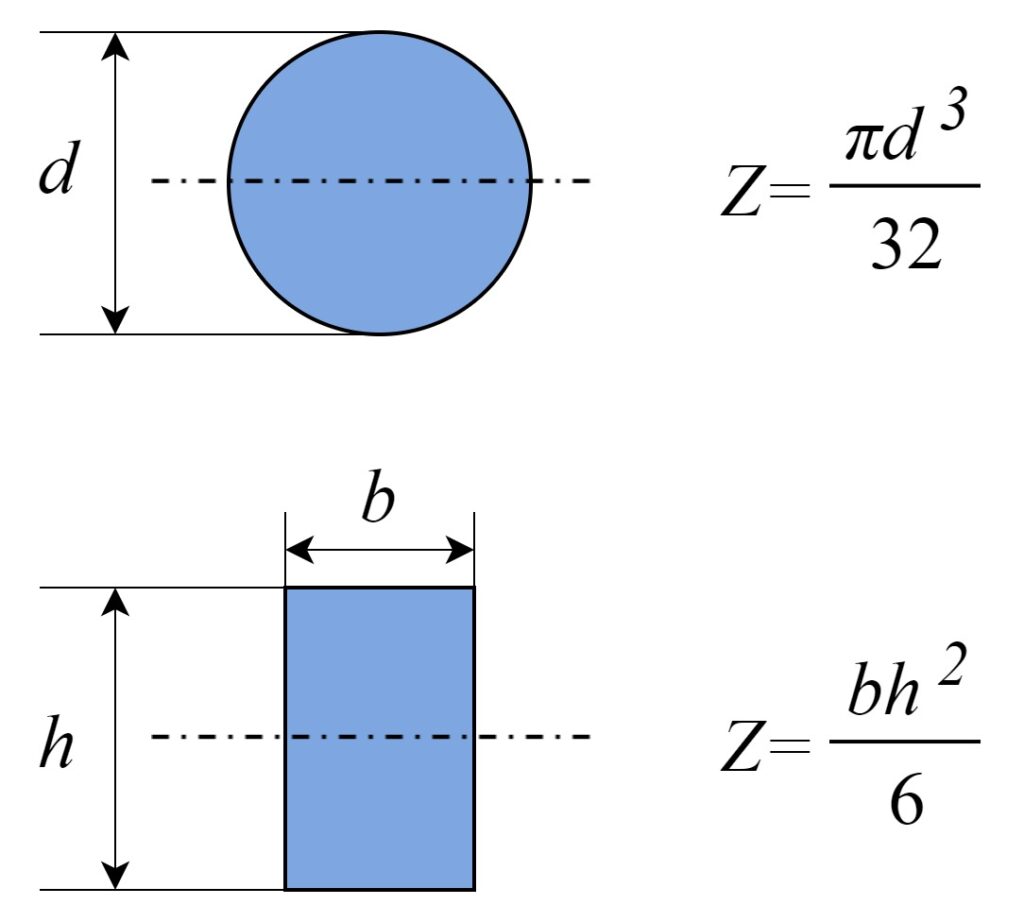
上で説明した断面二次モーメントの公式と比較すると、
\(I\)を中立軸から表面までの距離(\(d/2\)や\(h/2\))で割った
形になっているのが確認できます。
断面係数を使う場面
下の図のように断面二次モーメント\(I\)のはりに
曲げモーメント\(M\)を掛けたとき、軸方向の任意の位置\(y\)における応力\(\sigma\)は
次のように表されます。
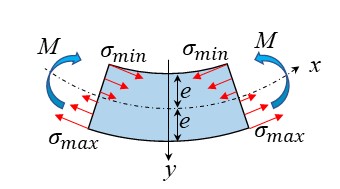
\(\sigma=\frac{My}{I}\)
中立面より上半分は圧縮、下半分は引っ張りの応力が掛かります。
最大応力\(\sigma_{max}\)と最小応力\(\sigma_{min}\)は符号が違うだけで絶対値は同じです。
中立面からの距離\(y\)が大きい方が応力\(\sigma\)が大きくなり、
\(y=e\)となる表面の位置において最大応力\(\sigma_{max}\)となります。
設計の実務においては、
「最も応力の高い表面の位置でも応力が許容値以下になるか?」を気にします。
つまり、表面の応力さえ分かれば、内部の応力はどうでもよいのです。
従って、\(y=e\)での応力値
$$\sigma=\frac{Me}{I}$$
を多用する事になります。ここで\(I\)、\(e\)は断面形状によって決まる物なので、
ひとまとめにして新たに\(Z=I/e\)という物理量を定義し、応力を
$$\sigma=\frac{M}{Z}$$
というシンプルな計算式で出せるように工夫した、というわけです。
断面係数\(Z\)が大きいほど、応力\(\sigma\)は小さくなります。
応力を下げてはりを壊れにくくしたければ、
断面係数\(Z\)の大きい形状にすれば良いのです。
「断面係数\(Z\)は、はりの応力求める際に使う」
という事がお分かり頂けましたでしょうか。
断面係数については、以下の記事でより詳しく解説しています。
梁の曲げを考える際、「断面係数」という物理量が登場します。 本記事では断面係数の意味・求め方を初学者でも分かるよう、図解を交えて詳しく解説します。 「断面係数」とは何か? 何を表しているのか 「断面係数」とはズ[…]
まとめ・比較表
混同しがちな「断面二次モーメント」と「断面係数」の違いを解説しました。
両者の違いを表にまとめます。
| 断面二次モーメント \(I\) | 断面係数 \(Z\) | |
|---|---|---|
| 意味合い | 曲げた時の変形しにくさ(硬さ) | 曲げた時の応力の立ちにくさ(強さ) |
| 使う場面 | はりのたわみ・変形量を求める | はりに掛かる応力を求める |
| 定義 | $$I=\int_{A}^{}y^2dA$$ \(A\):断面積、\(y\):中立軸からの距離 | $$Z=\frac{I}{e}$$ \(e\):中立軸から表面までの距離 |
| 公式 | 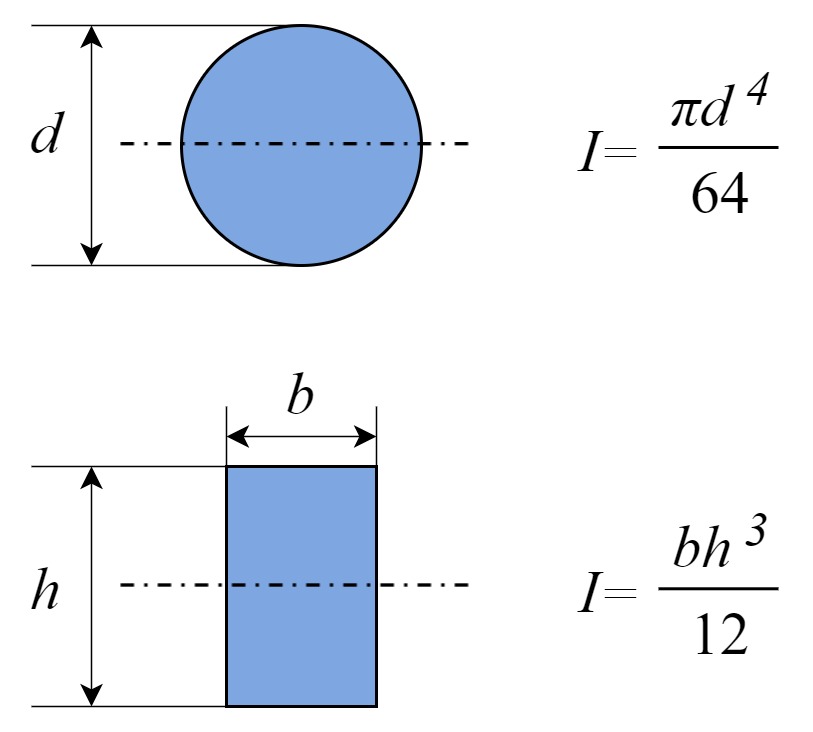 |  |
違いを理解して適切に使い分けましょう。