流体の物性値として「粘度」と「動粘度」があります。
定義が分かり難く、名前も似ているため取っ付き難いイメージが
あるかと思います。
本記事では「粘度」と「動粘度」の定義・計算方法・両者の違いを
詳しく解説します。
粘度(=粘性係数)とは
粘度のイメージ
粘度は別名で「粘性係数」とも呼ばれ、
流体の「さらさら」「ドロドロ」具合を表すものです。
例えば、コップに水を入れてスプーンでかき混ぜる場合と、
はちみつを入れてスプーンでかき混ぜる場合を比較します。
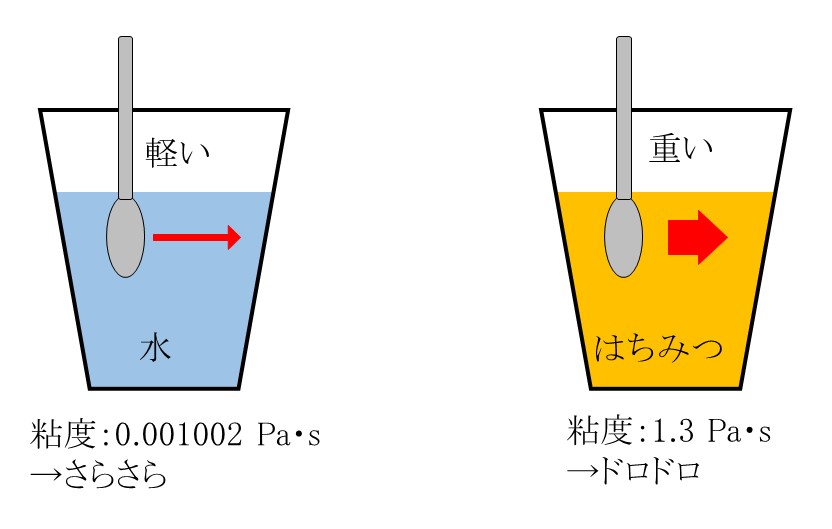
当然、はちみつを入れた時の方が重い(大きい力が必要)になります。
これは、はちみつの方が粘度が大きいためです。
粘度が大きい流体ほど「ドロドロ」、
小さい流体ほど「さらさら」になります。
粘度の定義式
粘度とは、「流体を変形させるときには変形速度に応じた力が必要になる」
という性質を表したものです。
下の図のように、間隔\(H\)が空いている2枚の平板間を流体で満たし、
上の1枚だけを速度\(U\)で平行に動かす場合を考えます。
速度分布を考えると、固定された下の平板付近の流体の速度は0、
上の平板付近の流体の速度は\(U\)となります。
平板の速度\(U\)が小さい場合には、速度分布は直線的となり、
これを「クウェット流れ」と呼びます。
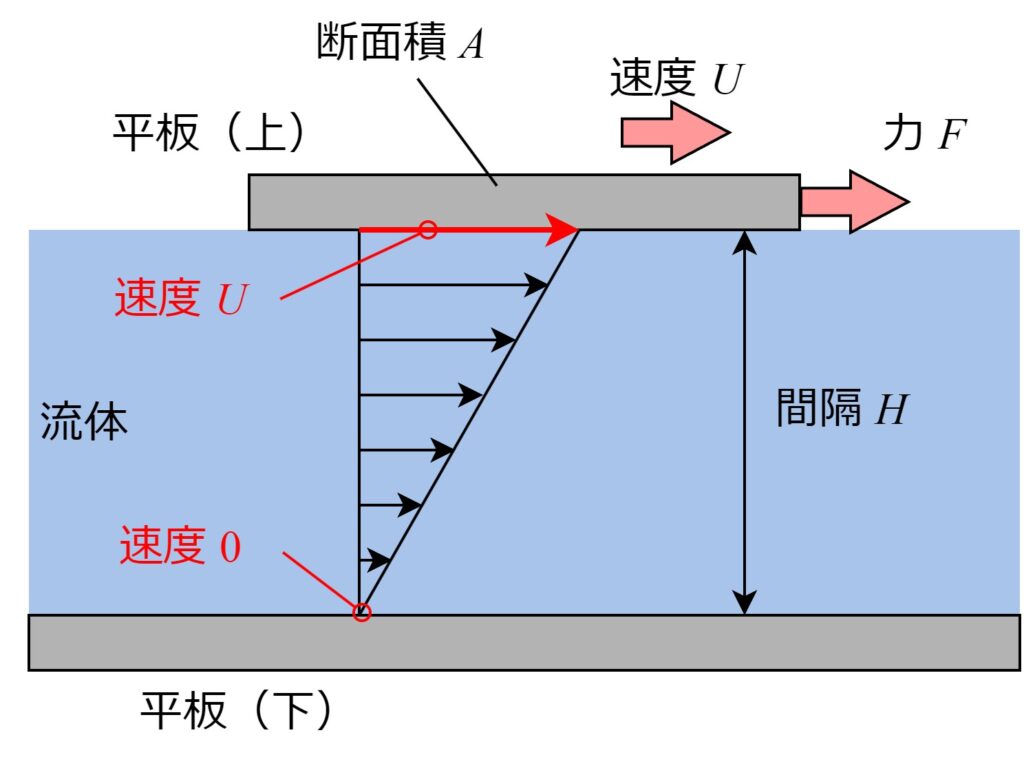
ここで平板に加える力を\(F\)、面積を\(A\)とすれば、
せん断応力\(\tau(\tau=F/A)\)は\(U/H\)に比例することが実験的に分かっています。
従って、
$$\tau=\mu \frac{U}{H}$$
と書けます。比例定数\(\mu\)を粘度(=粘性係数)といい、単位は\(\rm{[Pa・s]}\)を用います。
流体の種類、温度、圧力によって決まる物性値です。
一般的には、クウェット流れのように直線状の速度分布とは限らず、
下の図のように曲線状になります。
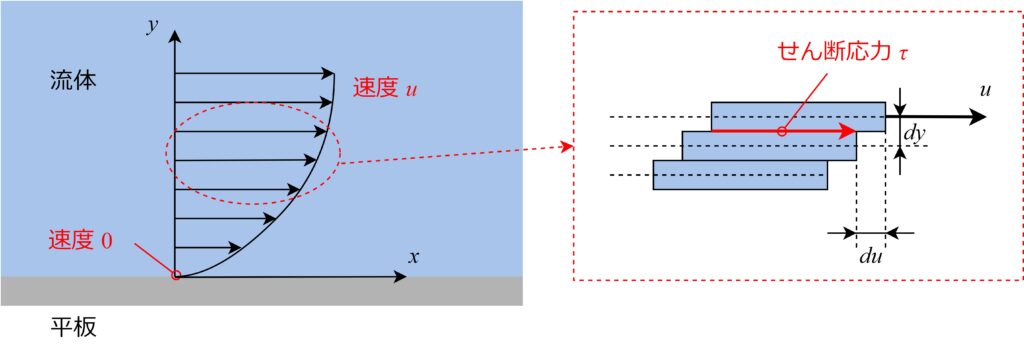
従って流体に働くせん断応力は次のように書けます。
$$\tau=\mu\frac{du}{dy}$$
これを「ニュートンの粘性法則」といい、粘度の定義式として一般に用いられます。
なお\(du/dy\)は速度勾配を表しており、上式は先ほど述べた
「流体を変形させるときには変形速度に応じた力が必要になる」
という性質を表している事が分かります。
粘度の温度依存性
粘度には温度依存性があり、液体と気体とで、温度と粘度の関係が逆になります。
液体
液体の場合、温度が上昇すると粘度が低下します。
液体の粘度は、液体の分子同士が引き合う力(分子間力)によって生じます。
温度が上昇すると液体の分子運動が活発になり、
分子が自由に動き回ろうとします。
すると分子同士が引き合う力に逆らい易くなり、粘度が低下します。
気体
気体の場合、温度が上昇すると粘度も上昇します。
気体は広い空間を分子が高速で飛び回っている状態で、
この分子同士が衝突して速度が平均化されることで
粘度が生じると言われています。
温度が上昇すると分子の運動がより高速になり、
衝突力・衝突頻度が増して粘度が上昇します。
動粘度(=動粘性係数)とは
動粘度のイメージ
動粘度は別名で「動粘性係数」とも呼ばれ、
「流れの伝わりにくさ」を表すものです。
動粘度を直感的にイメージすることは少し難しいですが、
例えば洗面器に流体を入れて、手でグルグルとかき回す場合を考えます。
水の場合は全体がグルグルと回りだし、渦になります。
子供の頃にお風呂で遊んだ事もあるかもしれません。
一方で空気の場合、グルグルと回る手の周辺には風が起こるかもしれませんが、
全体が渦になって回ることは考えにくいと思います。
はちみつを入れた場合では回す事すら不可能だと思います。
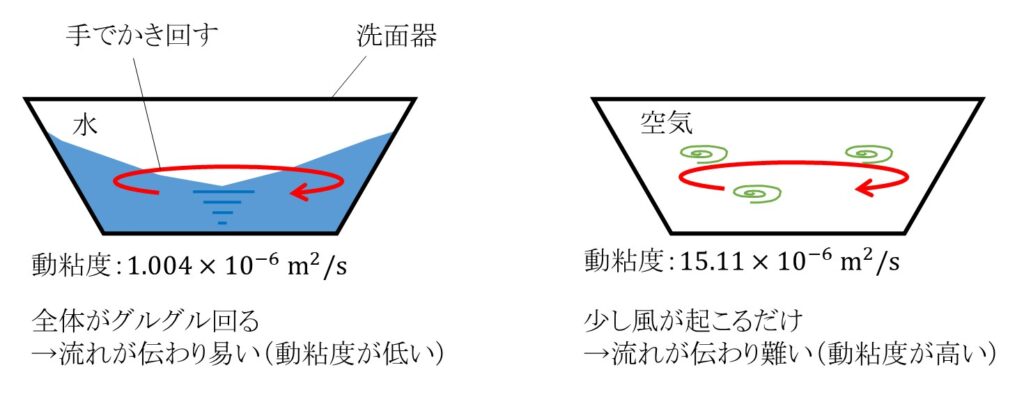
グルグルと全体が回る=流れが伝わり易い=動粘度が低い流体である、
とイメージすると良いです。
動粘度が高い流体ほど、流れが伝わりにくい流体となります。
動粘度の定義式
動粘度は「粘度」を「密度」で割って計算します。
$$\nu=\frac{\mu}{\rho}$$
単位は\(\rm{[m^2/s]}\)です。
流体の粘度が、流体の動き難さに与える影響を考えるために使われます。
動粘度が高い流体ほど動き難い(流れが伝わりにくい)流体となります。
なぜ「粘度」を「密度」で割るのか?
流体の動きを考える際に、なぜ「粘度」を「密度」で割った
「動粘度」を使うのかを考えます。
流体の粒子を車に例えると、動粘度は「車のブレーキの利き易さ」を表します。
粘度は「ブレーキ力」、密度は「車の重量」です。
ブレーキ力が同じでも、重い車はブレーキが利き難くなります。
ブレーキが利き難い車は止まり難い=流れが止まらず周囲に伝わり易い
という事になります。
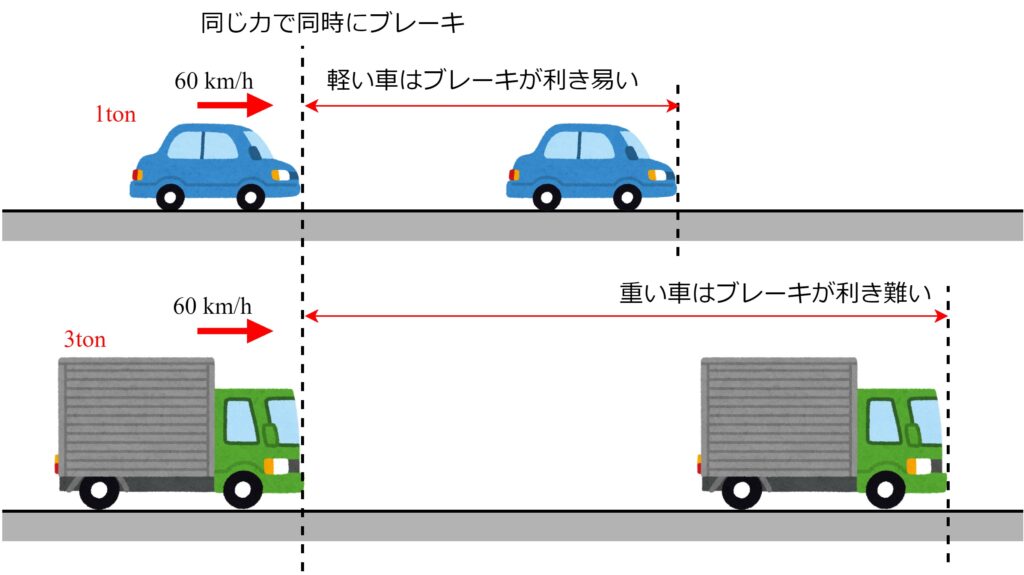
ブレーキ力だけでなく、車の重量も考慮した「ブレーキの利き易さ」
を考えた方が流体の動きを論じやすいため、動粘度が使われます。
「粘度」と「動粘度」の違いを表・グラフで解説
「粘度」と「動粘度」について解説してきましたので、
両者の違いをまとめます。
一言でいうと「粘度を密度で割ったものが動粘度」となりますが、
その他の違いについて表に記載しました。
| 粘度(=粘性係数) | 動粘度(=動粘性係数) | |
|---|---|---|
| 記号 | \(\mu\) | \(\nu\) |
| 単位 | \(\rm{[Pa・s]}\) | \(\rm{[m^2/s]}\) |
| 定義式 | $$\tau=\mu\frac{du}{dy}$$ (ニュートンの粘性法則) | $$\nu=\frac{\mu}{\rho}$$ (\(\rho\):密度) |
| イメージ | かき混ぜた時の抵抗力の大きさ | 流れの伝わりにくさ |
次に代表的な流体:水、乾燥空気、ギヤ油について粘度と動粘度を比較します。
1気圧、20℃の時、各流体の粘度・密度・動粘度は以下のようになります。
(ギヤ油の物性値は銘柄によって異なるので参考数値と捉えてください)
| 粘度\(\rm{[Pa・s]}\) | 密度\(\rm{[kg/m^3]}\) | 動粘度\(\rm{[m^2/s]}\) | |
|---|---|---|---|
| 水 | \(1.002×10^{-3}\) | \(998.22\) | \(1.004×10^{-6}\) |
| 乾燥空気 | \(1.822×10^{-5}\) | \(1.205\) | \(1.512×10^{-5}\) |
| ギヤ油 | \(7.258×10^5\) | \(896\) | \(8.100×10^2\) |
大小のイメージを掴みやすくするため、
対数目盛でグラフにすると以下のようになります。
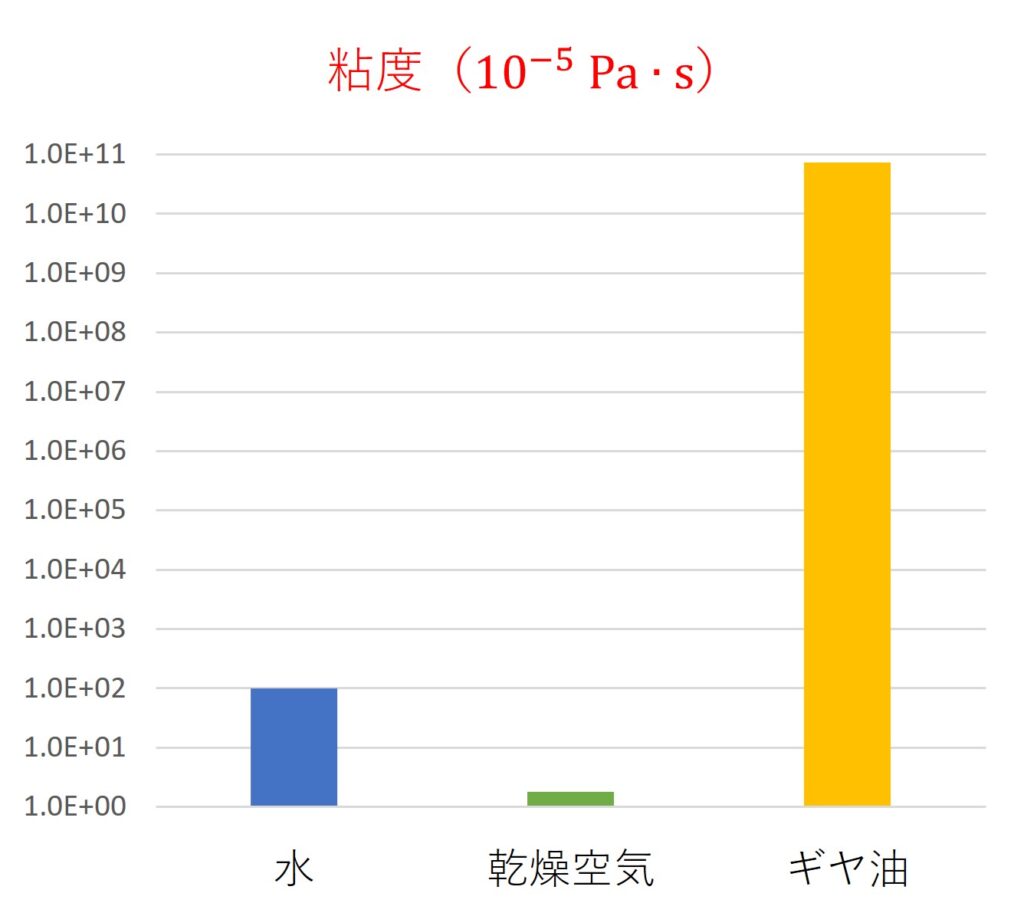
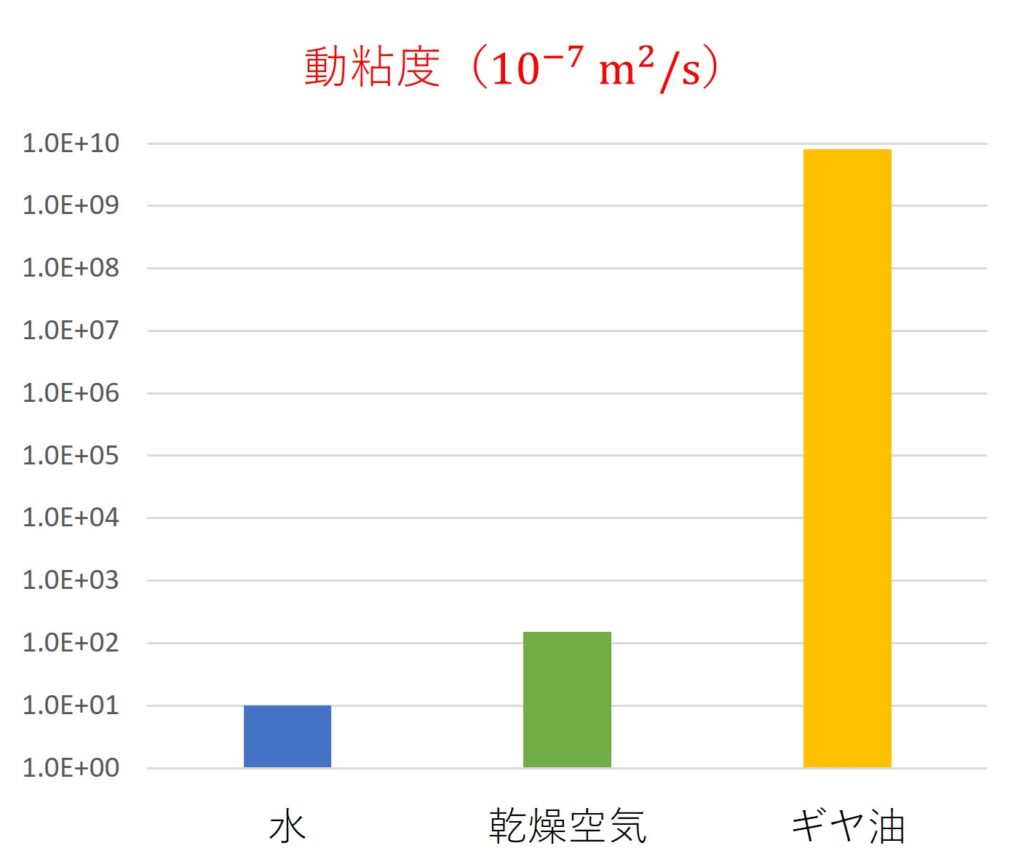
ギヤ油の粘度・動粘度が圧倒的に高いのは想像通りだと思います。
水と空気を比較すると、粘度は水の方が高い一方で、
動粘度は空気の方が高くなっています。
これは水の方が空気よりも密度が約1,000倍も大きいので、
粘度を密度で割ると大小が逆転するためです。
まとめ
「粘度」と「動粘度」について、定義・計算方法・両者の違いを解説しました。
ポイントをまとめます。
- 「粘度」は流体をかき混ぜた時の抵抗力を表し、ドロドロの流体ほど粘度が大きい
- 「動粘度」は流れの伝わりにくさを表し、粘度を密度で割って求める
- 粘度を密度で割るのは、密度が重い流体ほど止まり難い(流れが伝わり易い)
現象を表現するため
皆様の参考になれば幸いです。







