「断面二次モーメント」という言葉を聞いて、ピンとこない方もいるかもしれません。
材料力学や構造設計において頻繁に登場するこの概念は、梁や柱の設計において非常に重要な役割を果たします。
しかし、その専門的な響きから、理解が難しいと感じる方も多いのではないでしょうか。
本記事では、断面二次モーメントの基本的な意味から、計算方法、実際の用途までを、図解を交えて分かりやすく解説します。
「断面二次モーメント」とは?
断面二次モーメントの意味と定義
断面二次モーメントとは、物体を曲げようとする力に対して「どれだけ曲がりにくい形状か」を表す物理量です。記号は「\(I\)」で表し、材料力学や構造設計において、物体の変形量やたわみを求める際に使用します。
例えば下の図のように、幅が広い物体を横に寝かせた状態で曲げた場合と、縦に起こした状態で曲げた場合とでは、曲がりにくさが全く異なります。これは断面二次モーメント差によるものです。断面二次モーメントの大きい物体の方が曲がりにくい、という性質があります。
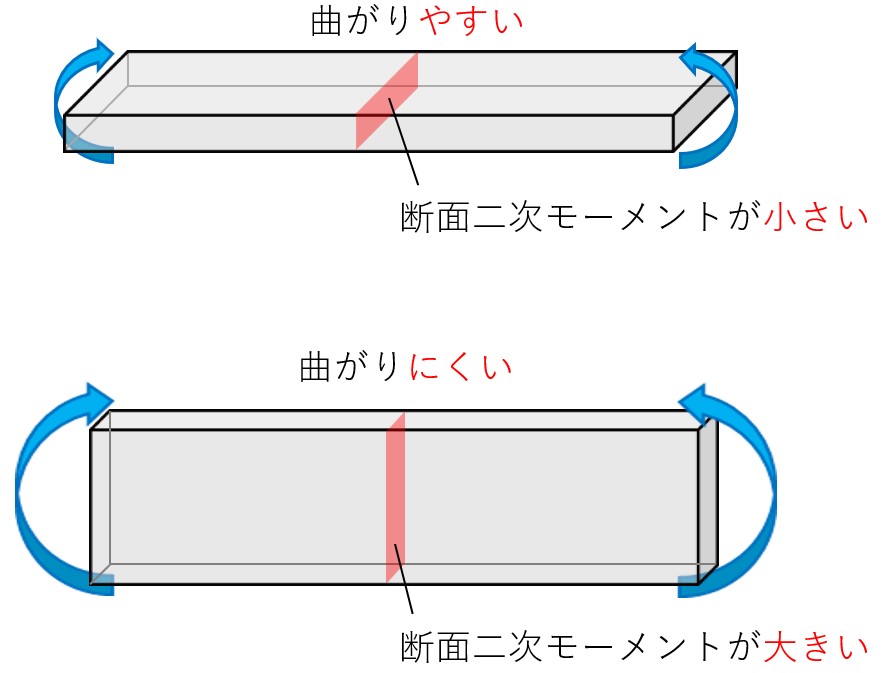
注意すべき点として、断面二次モーメントは断面の形状・寸法によって決まる値であり、材質などは全く関係しません。ゴムよりも金属の方が曲がりにくい、というような材質による違いは、ヤング率\(E\)という別の値で考慮されます。「同じ材質で比べた時にどれだけ曲がりにくい形状か」を表現できるよう、断面二次モーメント\(I\)とヤング率\(E\)は切り分けられています。
また、同じ形状であっても曲げる向きによって断面二次モーメントが異なります。上の例では、縦に起こした状態で曲げた方が断面二次モーメントが大きくなりました。これは「曲げる面に対して外側に面積が多い形状の方が断面二次モーメントが大きい」という、断面二次モーメントの計算方法に由来します。詳しくは後述します。
まとめると、断面二次モーメントとは、
- 物体を曲げようとする力に対して「どれだけ曲がり難い形状か」を表す
- 断面の形状・寸法によって決まる値であり、材質などは関係しない
- 曲げる面に対して外側に面積が多い形状の方が数値が大きくなり、曲がりにくい
という性質を持つ物理量となります。
断面二次モーメントの用途
断面二次モーメント\(I\)は、はりのたわみを求める際に使います。
例として、下図のような断面二次モーメント\(I\)、長さ\(\ell\)、ヤング率\(E\)の片持ちはりを考えます。このはりの先端に集中荷重\(P\)が掛かる場合、先端のたわみ\(y\)は次のように計算できます。

\(y=\frac{P\ell^3}{3EI}\)
たわみ\(y\)が、断面二次モーメント\(I\)に反比例する形となっています。従って、断面二次モーメント\(I\)が大きいほど、たわみ\(y\)が小さくなる事が分かります。
なお、たわみ\(y\)を求める計算式(たわみの公式)は、はりの固定方法や荷重のかけ方によって異なります。詳しくは以下の記事で解説しています。
梁に荷重が加わったとき、梁が変形する量を「たわみ」と言います。 本記事では、材料力学におけるたわみの求め方、試験等で役立つ公式の覚え方をわかりやすく解説します。 たわみとは 「たわみ」とは何か たわみとは、梁に[…]
梁に荷重が加わった時の変形量を「たわみ」と言います。たわみの大きさは公式を使えば簡単に計算する事ができますが、本記事では公式の導出方法・考え方を図解で分かりやすく解説します。 導出の流れを頭に入れておくと、試験で公式を忘れてしまった[…]
「断面二次モーメント」と「断面係数」の違い
断面二次モーメントと良く似た物理量として「断面係数」がありますが、別物ですので混同しないように注意しましょう。
- 断面二次モーメント\(I\):
「どれだけ曲がりにくい形状か」を表す。はりのたわみ・変形量を求める際に使う - 断面係数\(Z\):
「どれだけ応力が立ちにくい形状か」を表す。はりに掛かる応力を求める際に使う
計算に便利なように、断面二次モーメントと断面係数は式のまとめ方(定義)が少しだけ異なります。両者の違いについては以下の記事で詳しく解説しています。
材料力学では「断面二次モーメント」と「断面係数」が頻出しますが、名前も算出方法も似ているので混同し易いかと思います。 本記事では断面二次モーメントと断面係数の違いを分かり易く解説します。 断面二次モーメントと断面係数の違い[…]
また、断面係数の意味や求め方については、以下の記事で詳しく解説しています。
梁の曲げを考える際、「断面係数」という物理量が登場します。 本記事では断面係数の意味・求め方を初学者でも分かるよう、図解を交えて詳しく解説します。 「断面係数」とは何か? 何を表しているのか 「断面係数」とはズ[…]
断面二次モーメントの計算方法
計算の基本的な考え方
断面二次モーメント\(I\)は「断面の中心からどれだけ遠い位置に面積が集中するか」を数値化したものです。以下の式で計算できます:
$$I=\int_A y^2 dA$$
- \(dA\):物体の断面を構成する、微小部分の面積
- \(y\):中立軸(例:ビームの中央)から微小部分\(dA\)までの距離
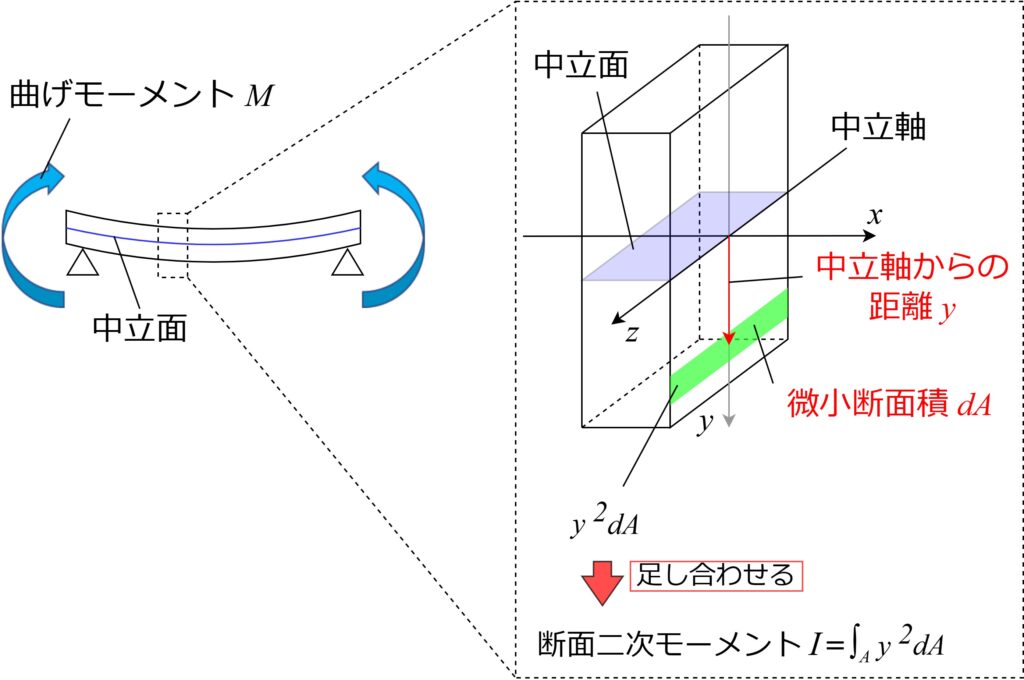
つまり、断面二次モーメントは「微小断面積\(dA\)×中立軸からの距離\(y\)の2乗」の総和となります。距離\(y\)が2乗で計算されているのがポイントで、遠い位置にある微小断面積\(dA\)が大きく影響する事になります。これは遠い位置にある断面の方が、曲げる力に対して強く踏ん張る事ができるためです。(詳しくは後述します)
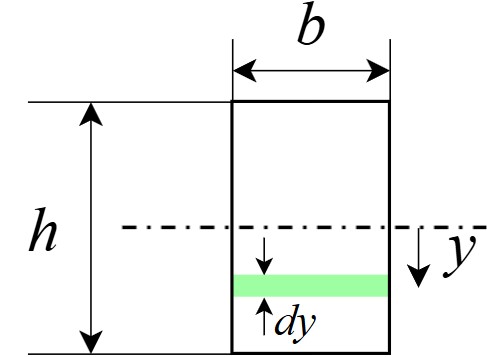
例として、下の図のような長方形断面の断面二次モーメントを計算してみます。微小断面積\(dA=b\times dy\)である事を考慮すると、以下のように計算できます。
$$I=\int_A y^2 dA=\int_{-\frac{h}{2}}^{\frac{h}{2}}y^2b\times dy=\frac{bh^3}{12}$$
ここで注目したいのは、断面二次モーメントの計算結果が、断面の高さ\(h\)の3乗に比例している事です。例えば断面の高さ\(h\)を2倍にすると、物体の曲がり難さを\(2^3=8\)倍にできる(たわみ量を1/8に低減できる)という事を意味します。断面二次モーメントは、断面の幅方向\(b\)の寸法よりも、高さ方向\(h\)の寸法に大きく影響されるのです。
断面二次モーメントの大きな形状とは?
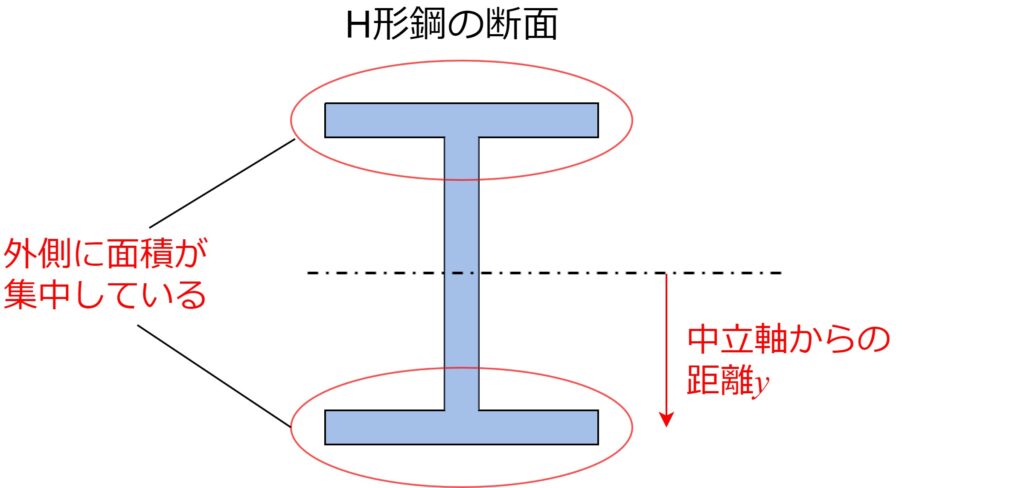
前述のように、断面二次モーメントは「微小断面積\(dA\)×中立軸からの距離\(y\)の2乗」の総和で計算されます。このため、中立軸から遠い位置(=外側)にいる微小断面積は、「距離の2乗」の影響で断面二次モーメントに大きく影響します。
従って断面積の合計が同じであっても、中立軸の外側に断面積が集中した形状ほど断面二次モーメントが大きく、曲げに対して有利となります。
この原理に則り、理にかなった形状をしているのがH形鋼です。
外側に断面積が集中しており、少ない材料で大きな断面二次モーメントを出すことが出来ます。
「二次モーメント」の意味は?なぜ距離の2乗を掛ける?
「断面二次モーメント」という単語の中の「二次モーメント」の意味を考えてみます。これは「モーメント」という概念とその「次数」に関係しています。
「モーメント」とは?
物理や工学における「モーメント」とは、ある基準点や軸からの距離と、その距離に作用する量(力や面積など)の積として定義されます。例えば力のモーメントは、力×距離で表され、どれくらいの回転力を持つかを表します。同じように、断面二次モーメントも「面積」に対してモーメントを求めたものです。
「二次」の意味は?
二次とは、距離の2乗を取ることを意味していますが、断面二次モーメントはなぜ距離を2乗して計算するのかについて解説します。下の図のような梁の微小部分において、どれだけの曲げモーメントを受けられるか考えます。
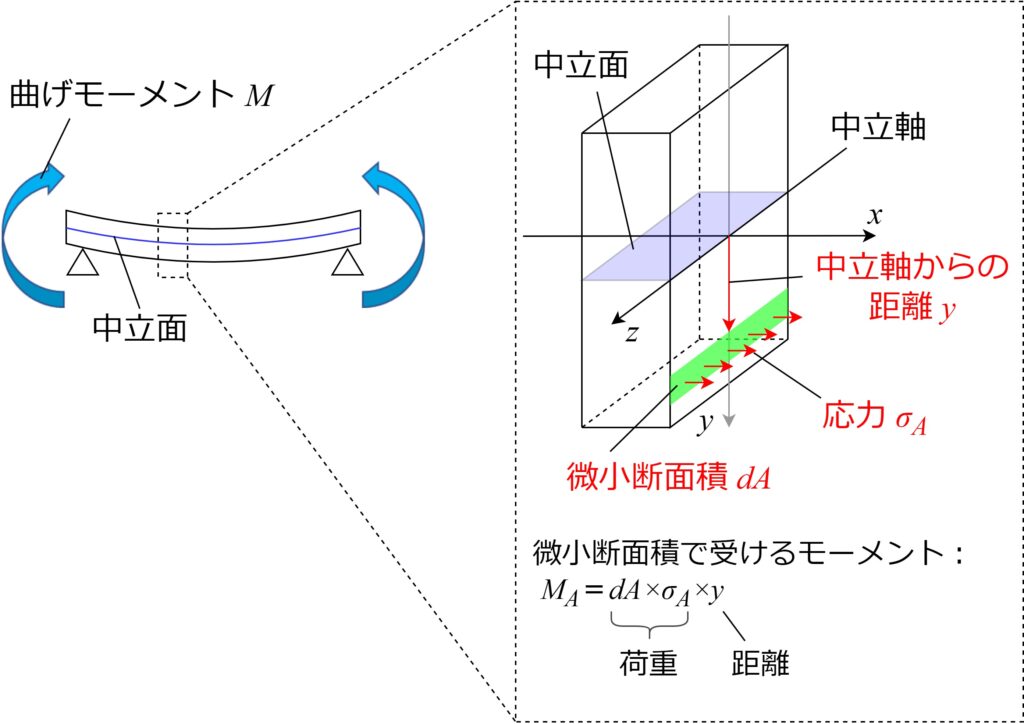
微小断面\(dA\)を考えたとき、この微小断面に掛かる応力を\(\sigma_A\)、受け持つ曲げモーメントを\(M_A\)と置きます。力のモーメントは「荷重」×「距離」なので、
$$M_A=(dA×\sigma_A)×y$$
となります。モーメントを考える時の距離\(y\)が出てきました。これが断面に掛ける距離\(y\)の2乗のうち、1つ目です。
次に距離\(y\)の2つ目ですが、微小断面に掛かる\(\sigma_A\)は下の図のように分布しており、距離\(y\)に比例しています。
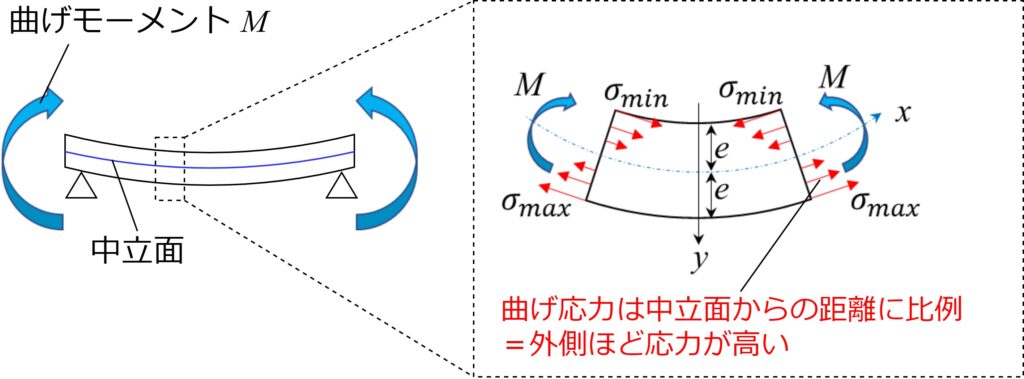
従って梁の外側の方が強く引っ張り・圧縮されます。表面に掛かる最大の応力を\(\sigma_{max}\)とすると、\(\sigma_{A}\)は以下で表されます。
$$\sigma_{A}=\sigma_{max}×\frac{y}{e}$$
これを踏まえて、微小断面\(dA\)で受け持つ曲げモーメント\(M_A\)は
$$M_A=dA×\sigma_{max}×\frac{1}{e}×y^2$$
と書き直す事ができ、距離\(y\)の2乗に比例した形になる事が分かります。
つまり、モーメントを考える時の「力」と「距離」の両方で中立軸(中立面)からの距離\(y\)が掛かるので、断面二次モーメントは距離\(y\)の2乗に比例するのです。
良く使う断面二次モーメントの公式
円形と長方形の断面二次モーメントの公式を示します。
どちらも頻繁に登場する公式なので覚えておくと便利です。
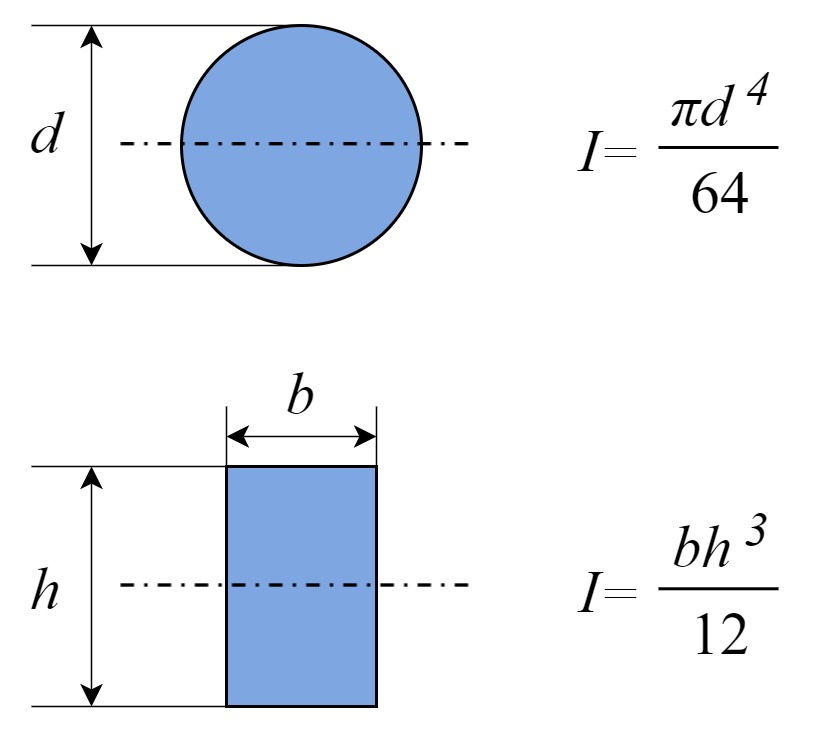
断面二次モーメントは「断面積」×「距離の2乗」の総和で計算される事から、距離の4乗の次元となっている事が分かります。
複雑形状の断面二次モーメントの求め方
断面二次モーメントを求める際に役立つ、基本的な考え方を2つ紹介します。以下を抑えておけば、複雑形状の断面二次モーメントも手計算で求める事ができます。
断面二次モーメントは「足し引き」できる
同一の中立軸を持つ断面であれば、断面二次モーメントを足し引きすることが出来ます。
例えば円筒形の断面二次モーメントは、中実の場合の断面二次モーメントから、中抜きされた分の断面二次モーメントを引き算する事で求められます。
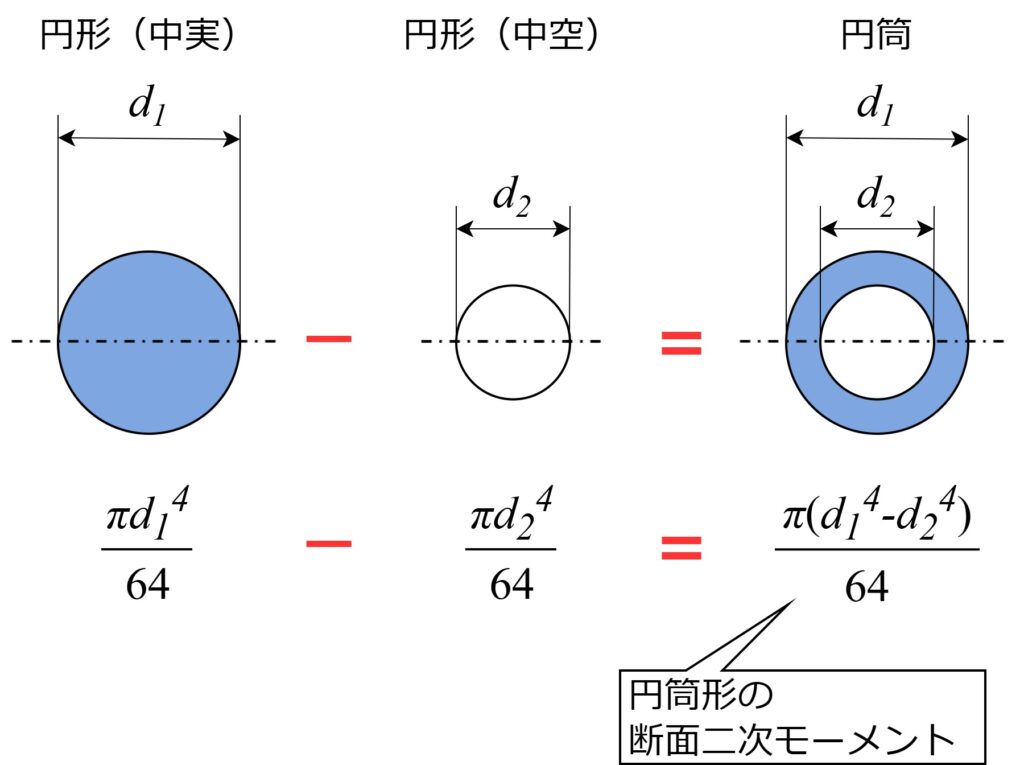
中空の長方形などの場合も同様の考え方で計算できます。
注意点として、「断面二次モーメント\(I\)」は足し引きできますが、「断面係数\(Z\)」は足し引きできません。複雑形状の断面係数を求める場合は、断面二次モーメントで足し引きした後に断面係数に換算する必要があります。
中立軸からズレた形状は「平行軸の定理」が便利
下の図のように断面が中立軸からズレた形状の場合は、「平行軸の定理」を使うと便利です。
元々の断面二次モーメント\(I\)に、「断面積」×「移動距離の2乗」を足す事で、ズレた後の断面二次モーメント\(I’\)を計算できます。
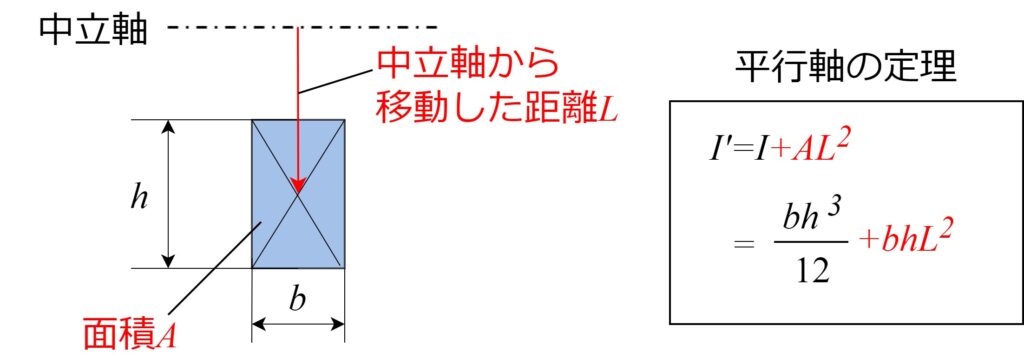
平行軸の定理を使えば、H形鋼の断面二次モーメントなども簡単に求める事ができます。
まとめ
断面二次モーメントの意味、計算方法、用途を解説しました。
本記事のポイントをまとめます。
- 断面二次モーメントとは、物体を曲げようとする力に対して「どれだけ曲がり難い形状か」を表す物理量
- 断面の形状・寸法によって決まる値であり、材質などは関係しない
- 曲げる面に対して外側に面積が多い形状の方が数値が大きくなり、曲がりにくい
- 断面二次モーメントが分かれば、物体の変形量やたわみを計算できる
皆様の参考になれば幸いです。







