梁の曲げ問題ではせん断力と曲げモーメントを求め、その分布をグラフにした「せん断力図」と「曲げモーメント図」を作成します。
本記事では、せん断力図と曲げモーメント図の描き方と、試験等でも役立つ「覚えておくべきグラフの特徴5つ」を解説します。
「せん断力」と「曲げモーメント」とは
梁には「せん断力」と「曲げモーメント」が作用する
荷重を受ける梁の断面には、「せん断力」と「曲げモーメント」が働きます。
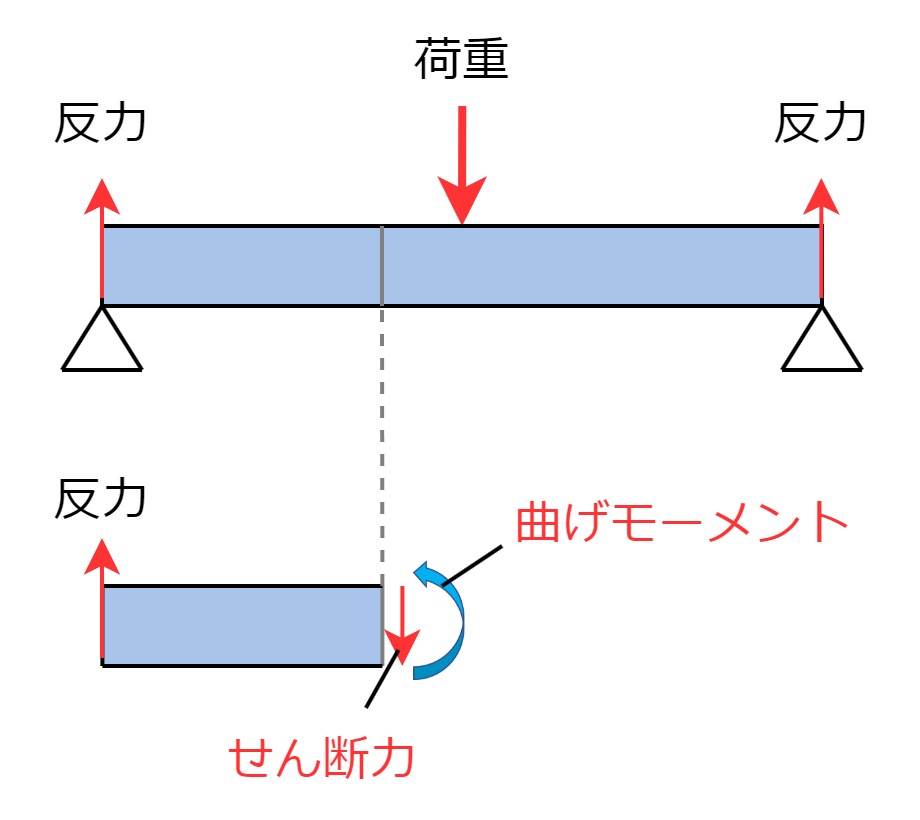
設計においては、せん断力と曲げモーメントを両方求め、「どちらでも壊れない事」を確認していきます。
せん断力とは
せん断力とは、部材を「互い違い」にずらすような内力のことです。
下図のように梁を分割して考えた時、各断面は矢印の方向に内力を受ける事で形が釣り合っています。これがせん断力です。
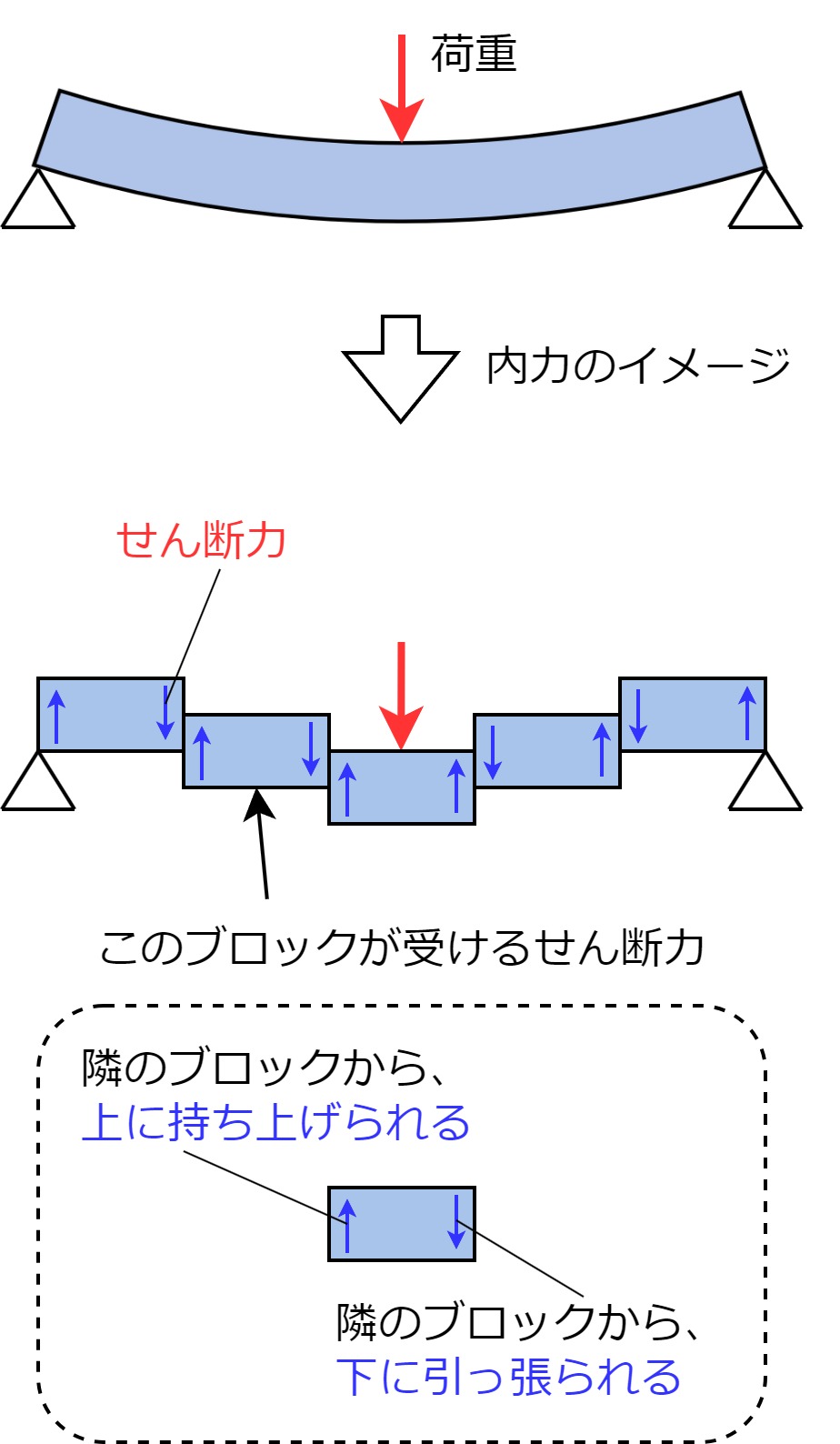
せん断力については、別の記事で詳しく解説しています。
物体内の二つの平面が互いにずれるような変形を「せん断」と言い、この時にかかる力を「せん断力」と言います。機械設計においては曲げや引張と合わせて、せん断についての考慮も欠かせません。 本記事では、せん断力の意味・求め方・許容値など[…]
曲げモーメントとは
曲げモーメントとは、部材を曲げようとする内力のことです。
少し厳密に言うと、曲げられた部材の内部に発生する「断面を回転させるモーメント」のことです。
なぜ、部材を曲げようとする内力をモーメントで表すのかを簡単に説明します。
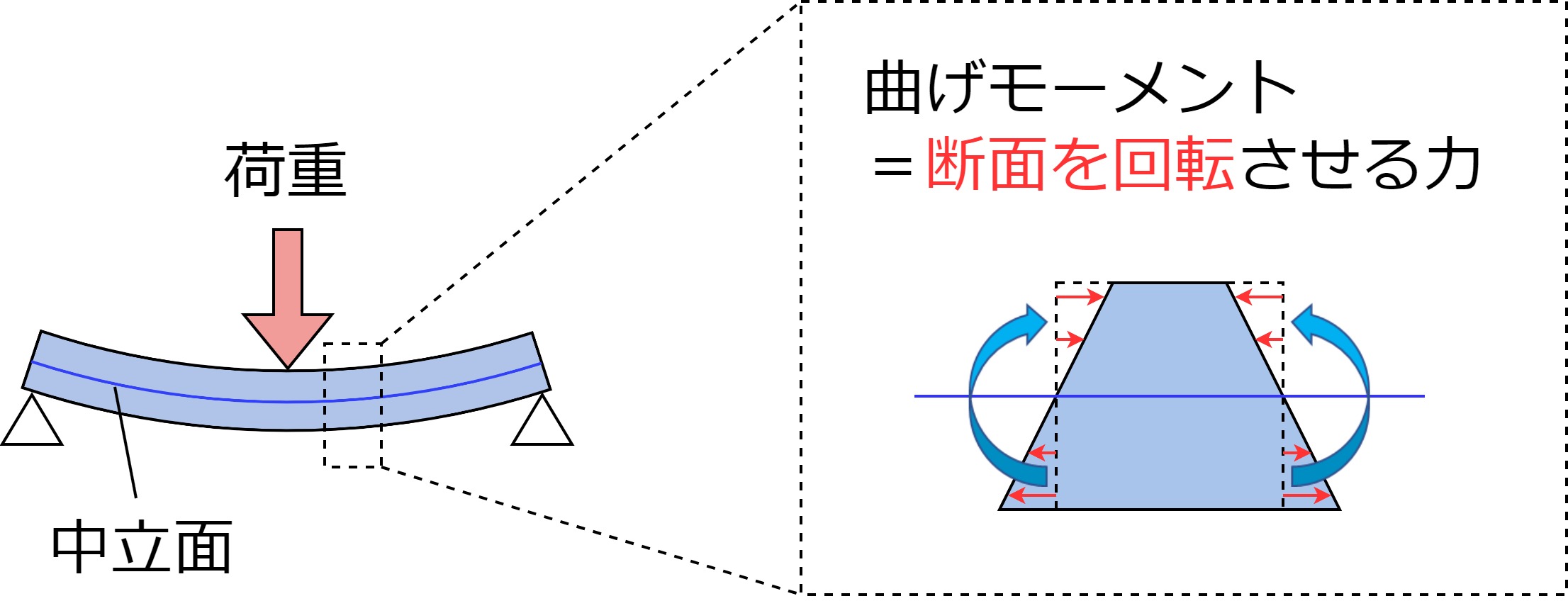
上図のように梁を曲げたときの微小部分を考えます。
梁全体は弓なりに曲がっているので、その微小部分は右のように少しずつ断面が上向きになるよう変形している事になります。この変形させる力が、断面を中央周りに回転させるように働いているので、梁を曲げる力を、曲げ「モーメント」と呼ぶのです。
曲げモーメントについては、別の記事で詳しく解説しています。
梁の曲げを考える際には「曲げモーメント」が登場します。 言葉の分かりやすさから、理解した気になりやすい曲げモーメント。 本記事では、そんな曲げモーメントの考え方・計算方法・公式について一からわかりやすく解説します。 […]
正負の考え方
せん断力と曲げモーメントには、正負の方向にお約束があります。
イメージとしては、最もシンプルな梁である単純梁（両端支持梁とも言います）に荷重を掛けた時に、「原点寄りの左側のブロックが受ける力の方向が正」と考えると覚えやすいです。
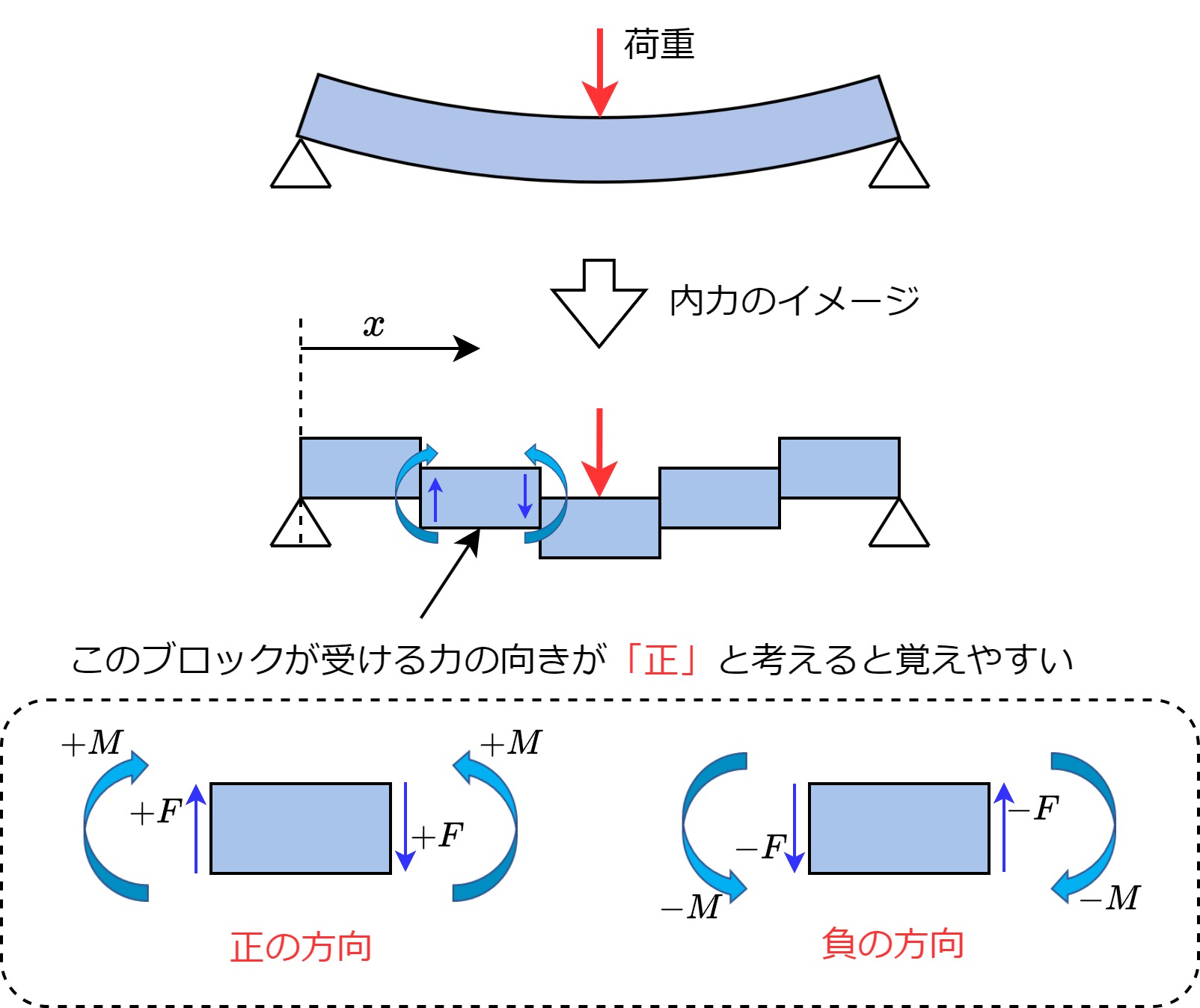
下向きに荷重を掛けた場合を正とする事に始めは違和感があるかもしれませんが、梁は重力の方向に荷重を受ける事が一般的なので、設計上この方が都合が良いのです。
符号を間違えると、下向きに荷重を加えているのに上方向に梁が持ち上がる、というおかしな結果になるので、細心の注意が必要になります。
「せん断力」と「曲げモーメント」の求め方を4つのStepで解説
梁の曲げ問題では、せん断力と曲げモーメントはセットで求めます。
求め方のステップは以下の通りです。
- 梁全体の力とモーメントの釣り合いより、支持反力を求める
- 任意の位置で梁を仮想的に切断し、2分割にする
- 切り離された梁における力とモーメントの釣り合いを解く
- せん断力図と曲げモーメント図を描く
下図の梁を例に、順を追って説明します。
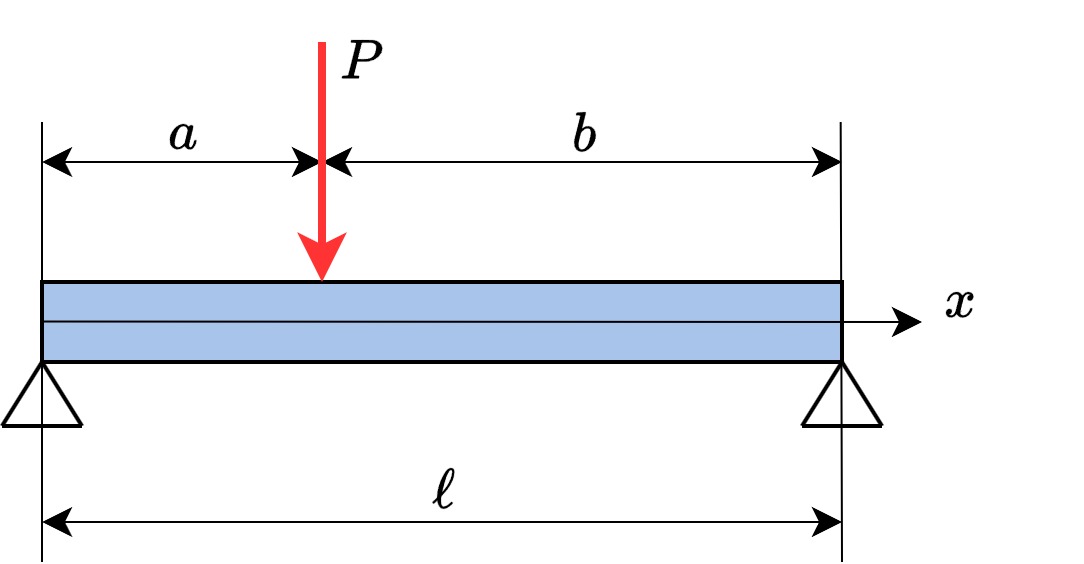
【Step①】梁全体の力とモーメントの釣り合いより、支持反力を求める
梁は荷重\(P\)を受けるだけでなく、支持点からの反力を受けて釣り合いを保っています。まずは梁全体の力とモーメントの釣り合いより、全ての支持点から受ける反力を求めます。
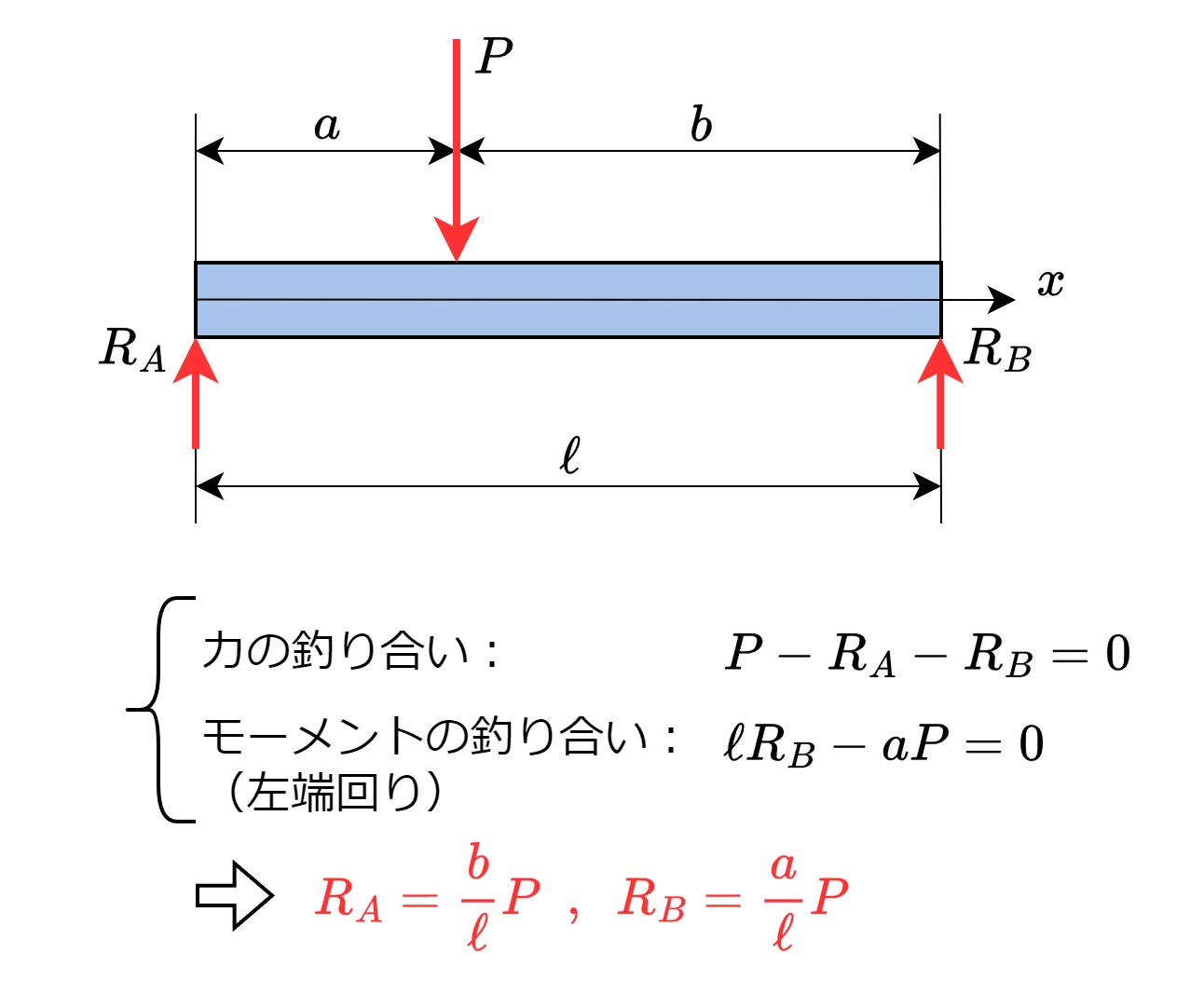
【Step②】任意の位置で梁を仮想的に切断し、2分割にする
梁の左端を原点とし、距離\(x\ (x<a)\)離れた位置のせん断力・曲げモーメントを求めていきます。
まずはこの位置で梁を仮想的に切断し、2分割にします。断面にはせん断力\(F\)と曲げモーメント\(M\)が、上述した「正の方向」に働いていると仮定して矢印を書きます。ここで逆方向に書いてしまうと、後の計算で正負を間違う事になります。
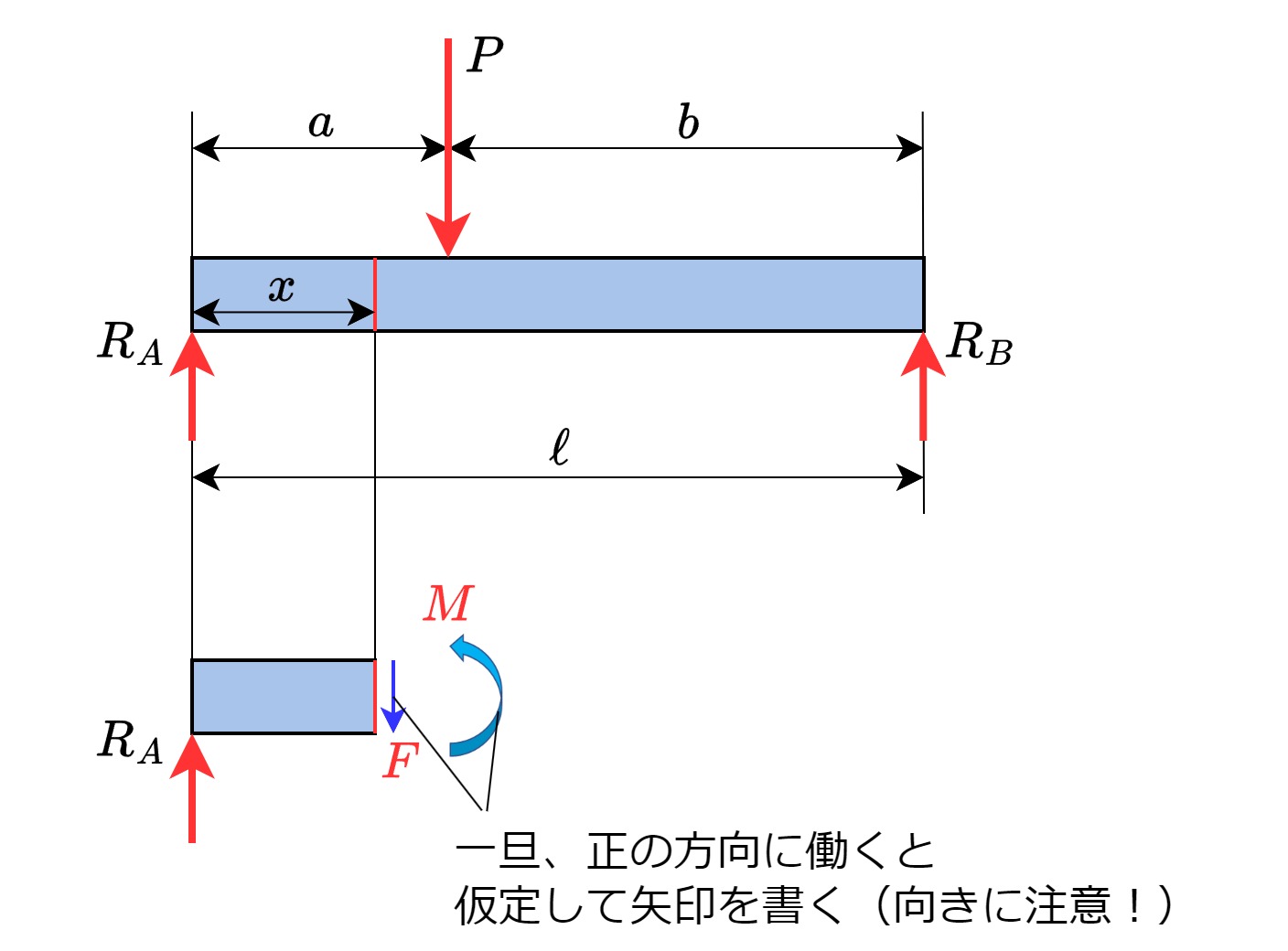
【Step③】切り離された梁における力とモーメントの釣り合いを解く
切り離された梁（左右どちらでも可）における力とモーメントの釣り合いから、せん断力\(F\)と曲げモーメント\(M\)を求めます。
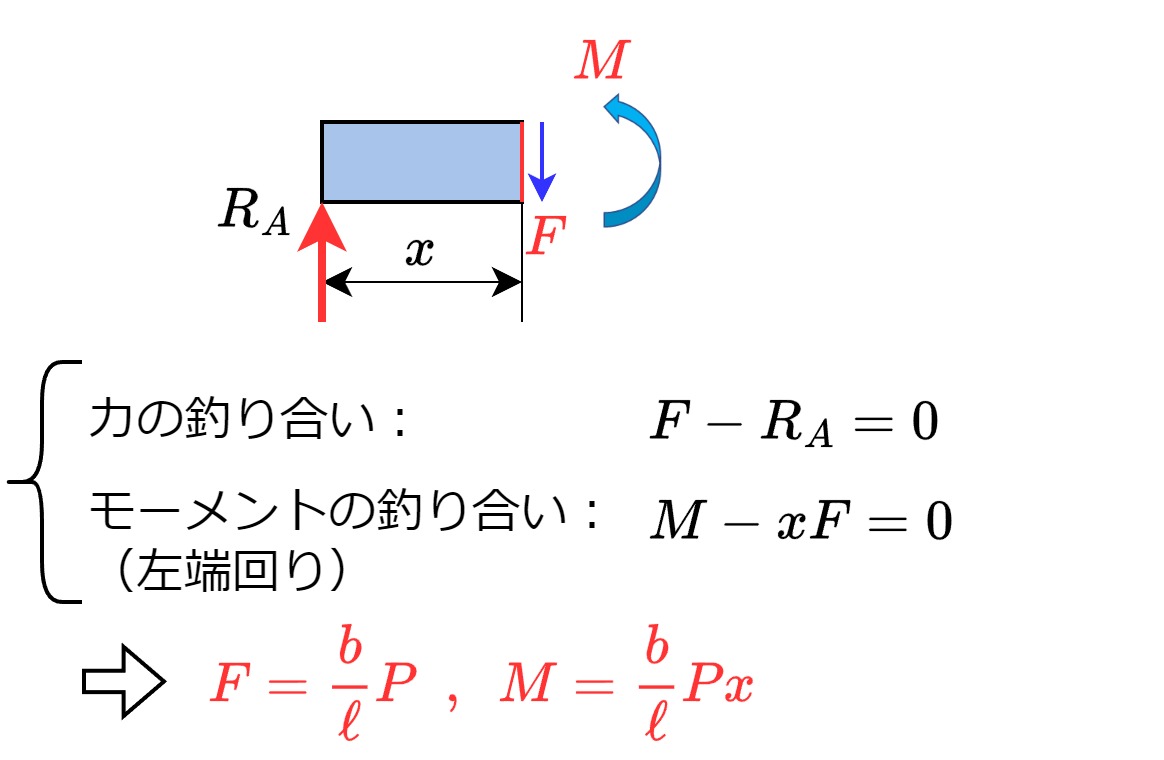
以上で、この切断位置におけるせん断力\(F\)と曲げモーメント\(M\)を求める事ができました。
同様に\(x>a\)の位置におけるせん断力\(F\)と曲げモーメント\(M\)も求めます。
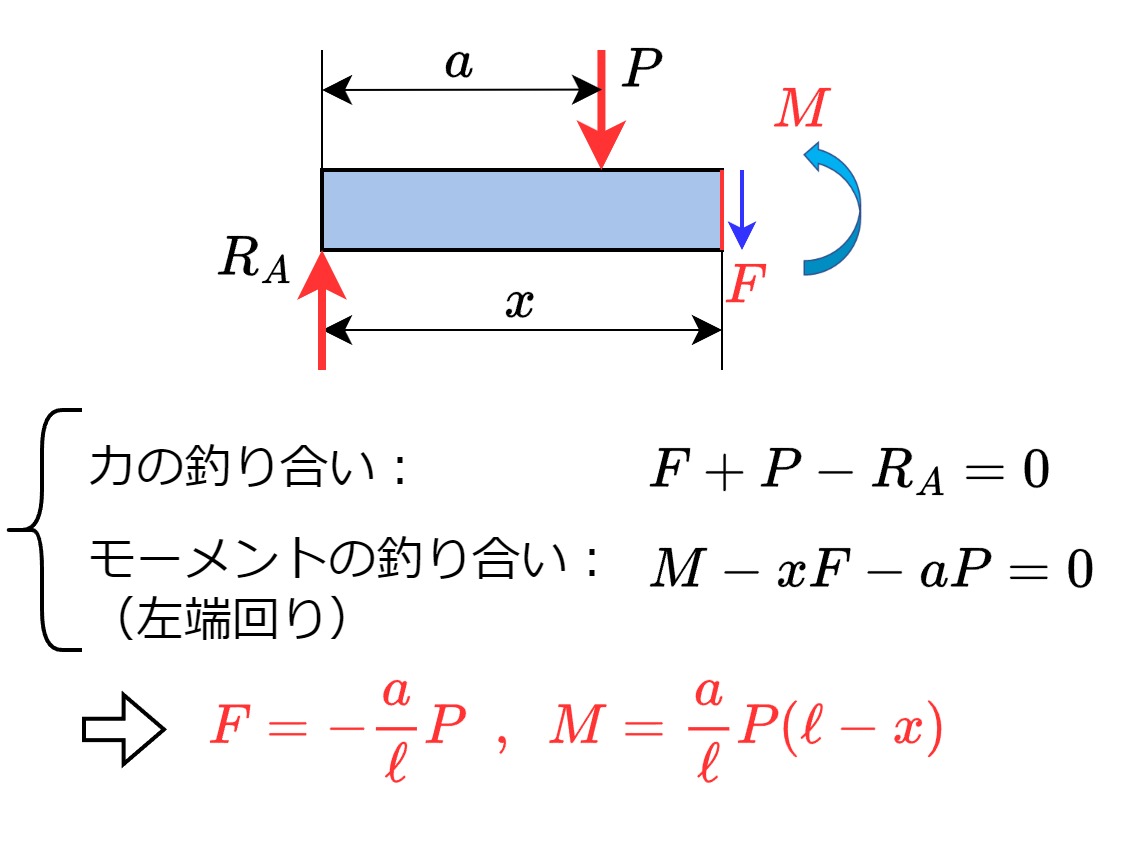
なお、同じ切断面を逆側（右側）の梁から解いた場合でも計算結果は同じになります。ただし断面が左側に来るとせん断力\(F\)と曲げモーメント\(M\)の正方向が変わる事に注意してください。
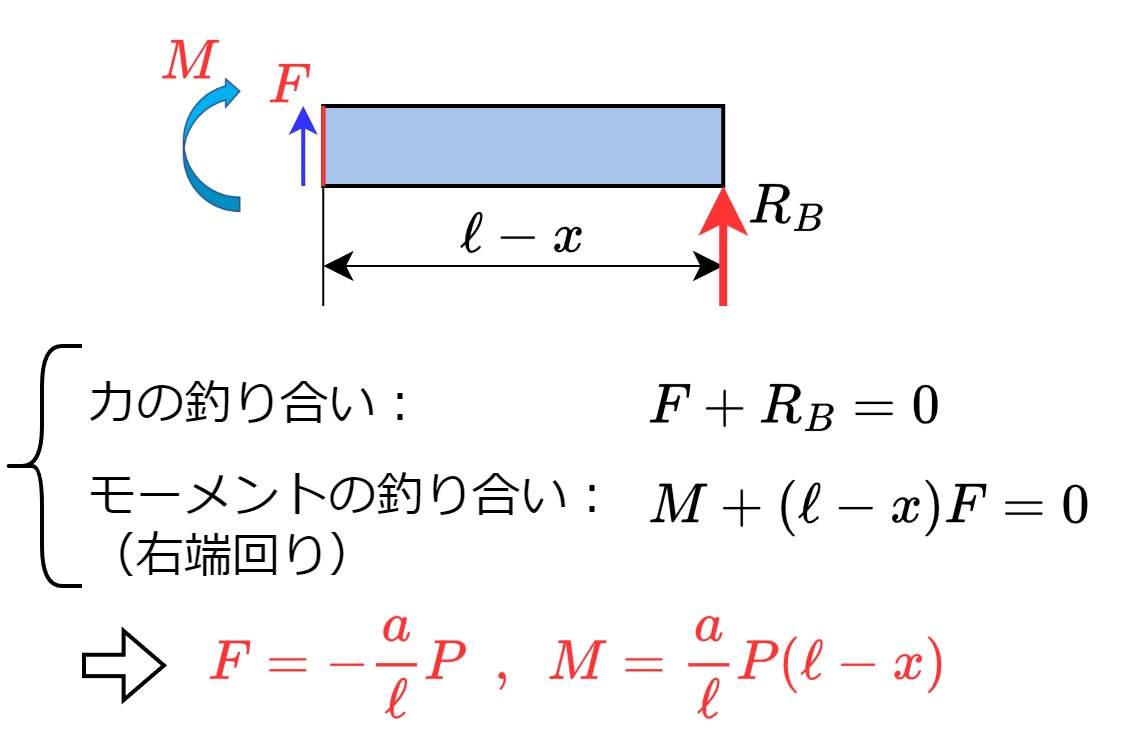
【Step④】せん断力図と曲げモーメント図を描く
最後に、求めたせん断力\(F\)と曲げモーメント\(M\)を、それぞれグラフにします。これらをせん断力図、曲げモーメント図と呼びます。詳細については後述します。
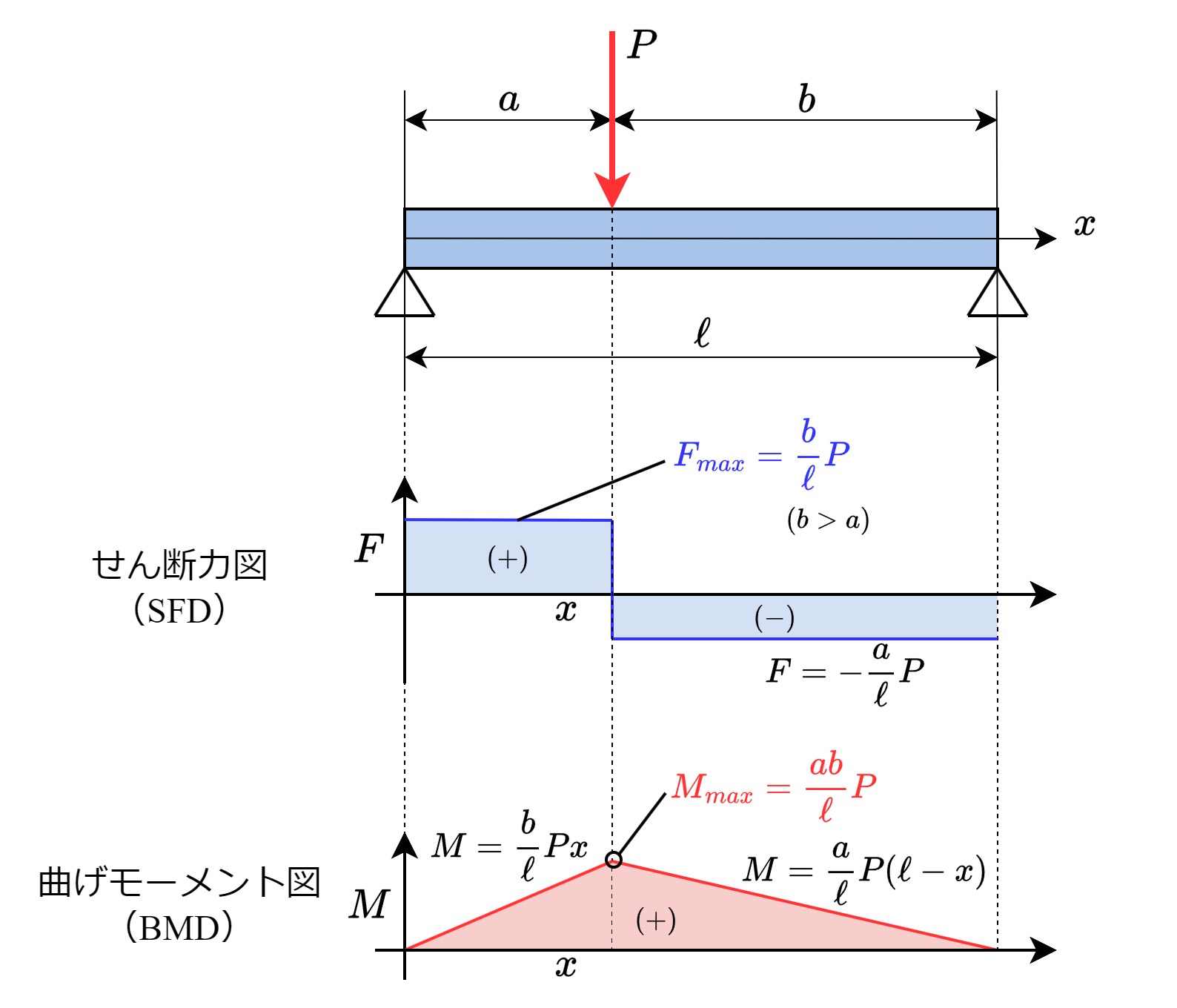
せん断力図（SFD）と曲げモーメント図（BMD）
せん断力図（SFD）・曲げモーメント図（BMD）とは
梁に掛かるせん断力\(F\)と曲げモーメント\(M\)は、切断位置\(x\)によって変化します。この関係を見易く図示したものが、せん断力図と曲げモーメント図です。
せん断力図はSFD（Shearing Force Diagramの略）、曲げモーメント図はBMD（Bending Moment Diagramの略）とも呼ばれます。
せん断力図・曲げモーメント図を描くことで、「最も大きな力が掛かる位置」が一目瞭然となります。
SFD・BMDと公式の一覧
様々な梁におけるせん断力図（SFD）・曲げモーメント図（BMD）と、最大値の公式を示します。
| 梁の種類・SFD・BMD | せん断力\(F\)・曲げモーメント\(M\)の式 |
|---|---|
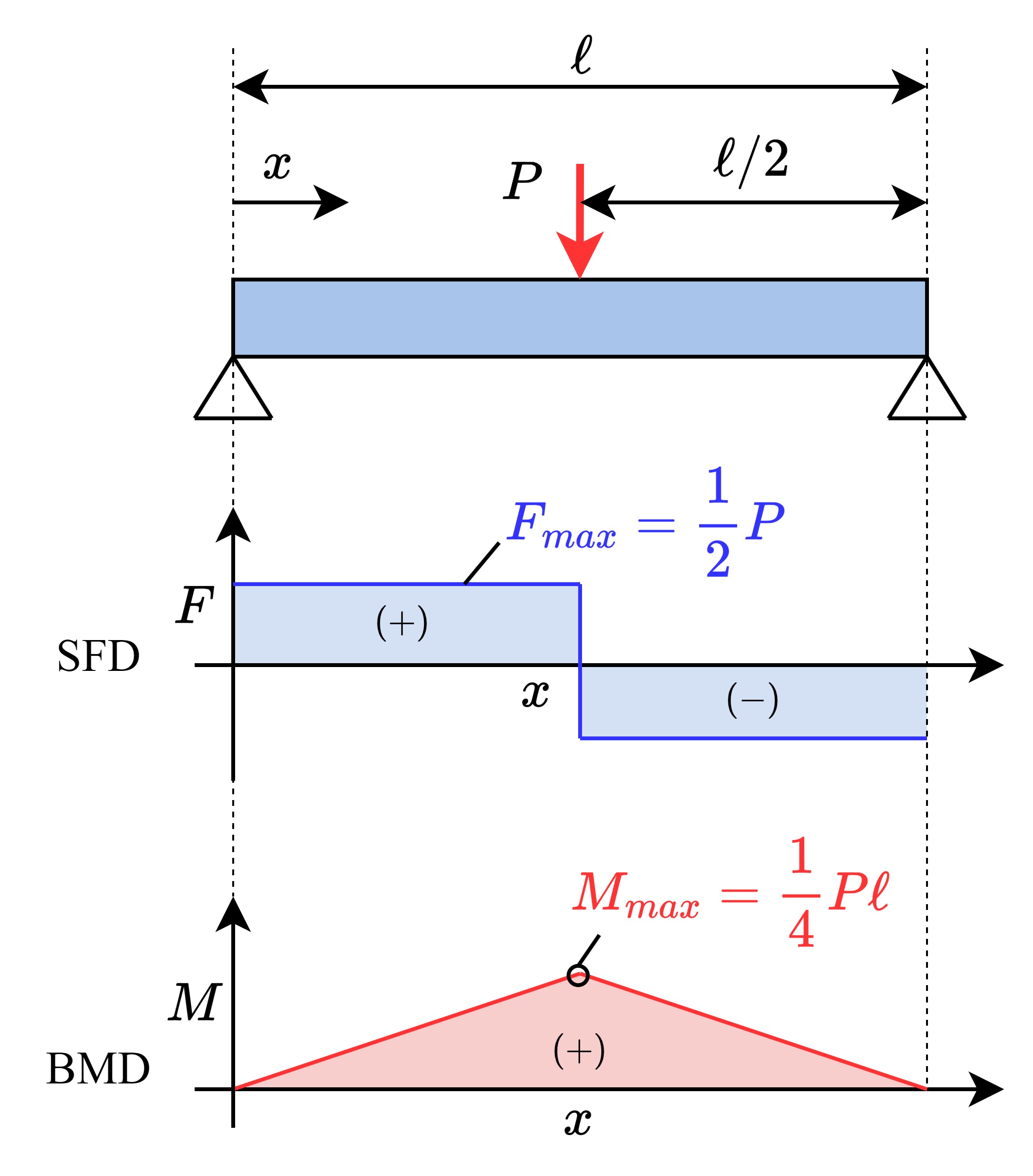 | \(F= \begin{cases}\displaystyle\frac{1}{2}P&\displaystyle(0\leq x \leq \frac{\ell}{2}) \\ \\ -\displaystyle\frac{1}{2}P&\displaystyle(\frac{\ell}{2}\leq x \leq \ell) \end{cases} \) \(M= \begin{cases}\displaystyle\frac{1}{2}Px&\displaystyle(0\leq x \leq \frac{\ell}{2}) \\ \\ \displaystyle\frac{1}{2}P(\ell-x)&\displaystyle(\frac{\ell}{2}\leq x \leq \ell) \end{cases} \) |
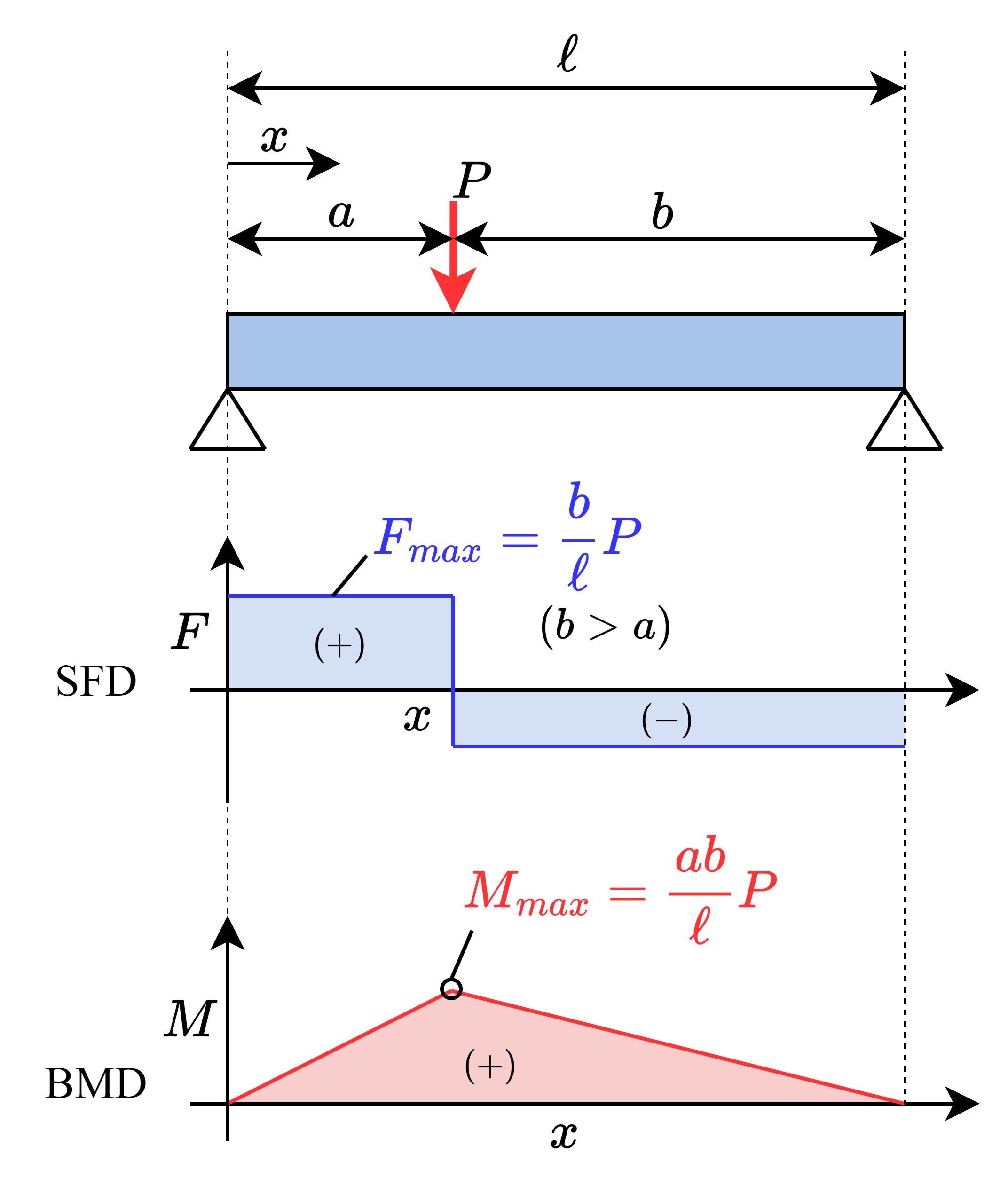 | \(F= \begin{cases}\displaystyle\frac{b}{\ell}P&\displaystyle(0\leq x \leq a) \\ \\ -\displaystyle\frac{a}{\ell}P&\displaystyle(a\leq x \leq \ell) \end{cases} \) \(M= \begin{cases}\displaystyle\frac{b}{\ell}Px&\displaystyle(0\leq x \leq a) \\ \\ \displaystyle\frac{a}{\ell}P(\ell-x)&\displaystyle(a\leq x \leq \ell) \end{cases} \) |
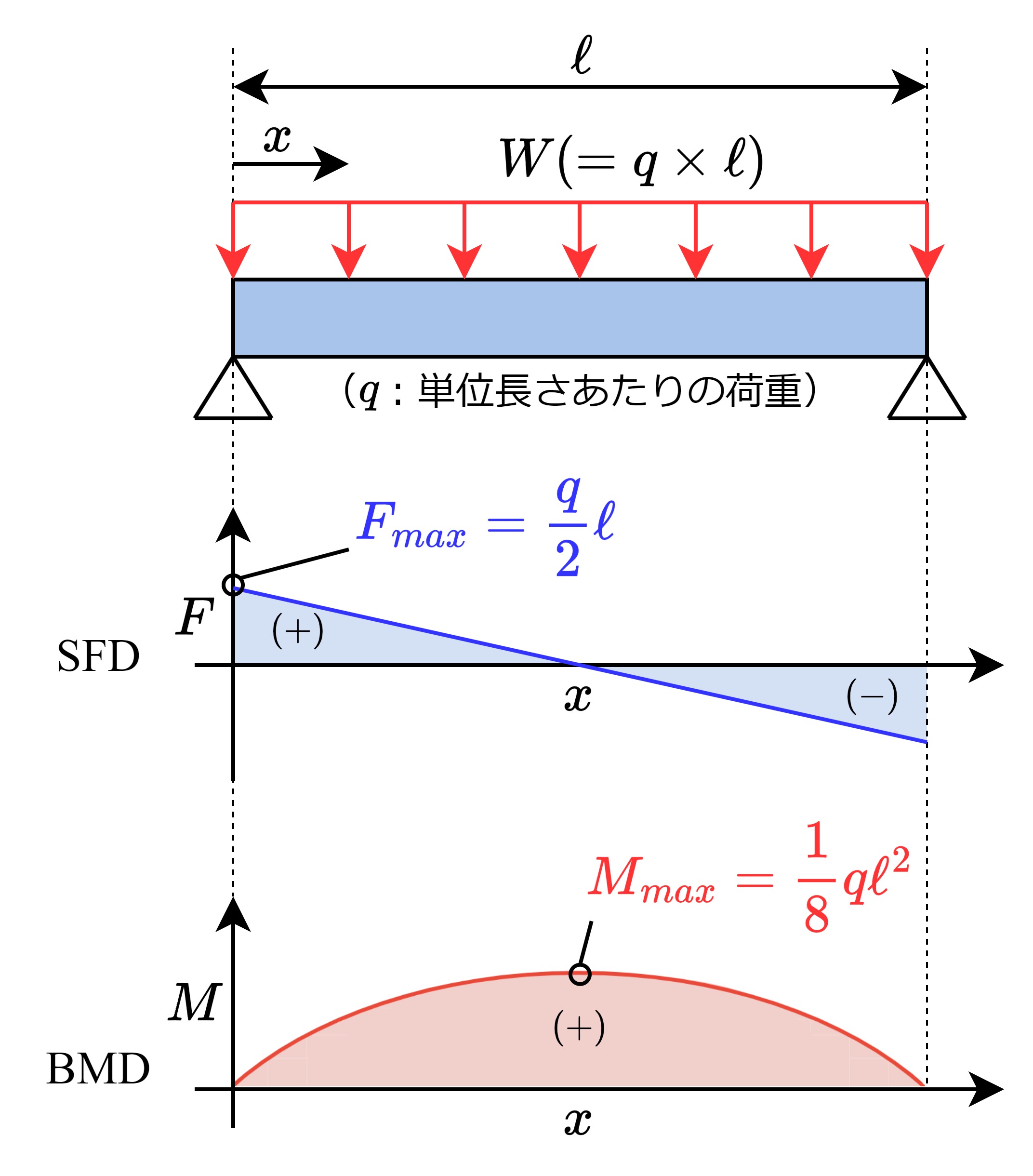 | \(\displaystyle F=q\left(\frac{\ell}{2}-x\right)\) \(\displaystyle M=\frac{1}{2}qx(\ell-x)\) |
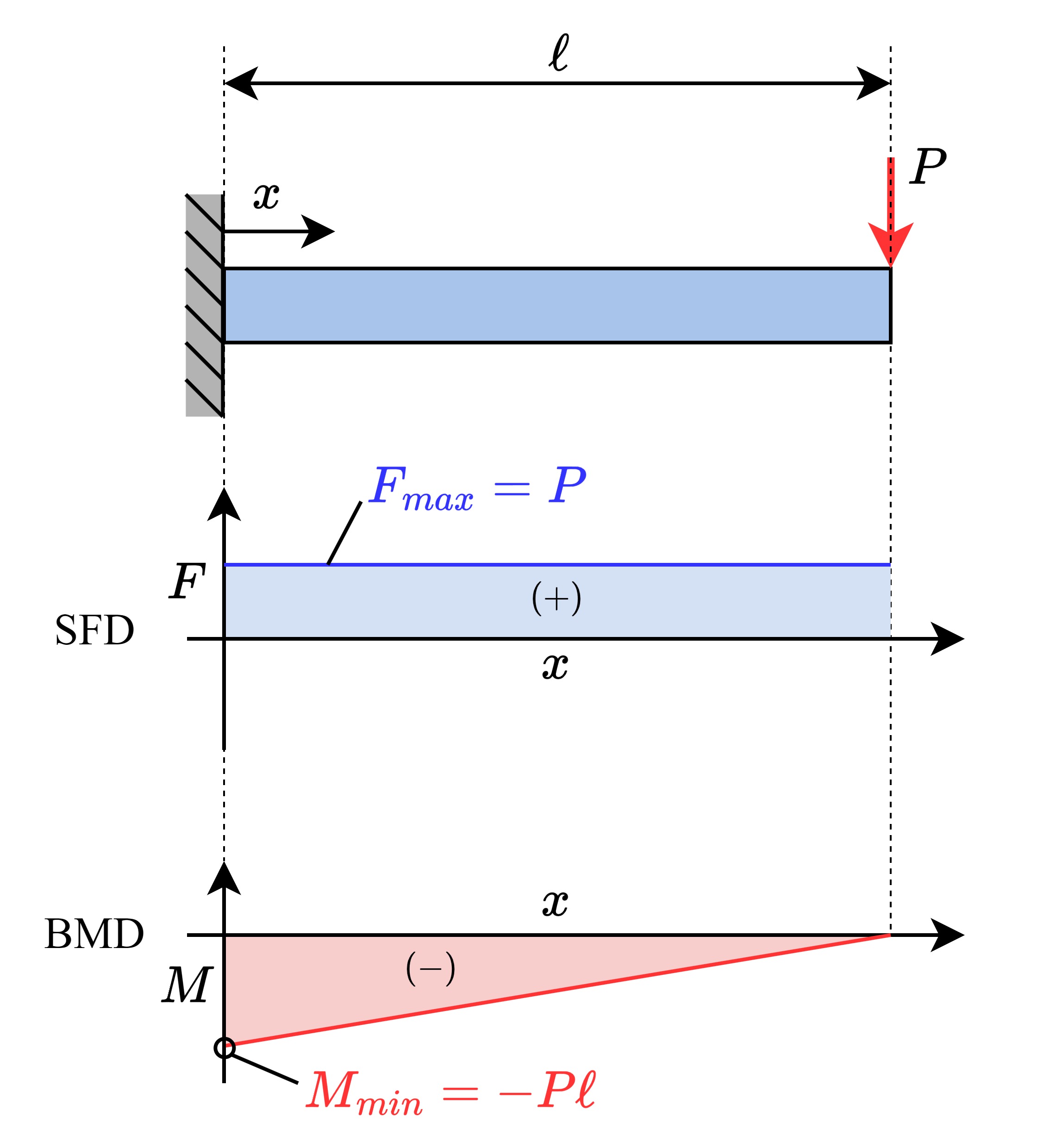 | \(\displaystyle F=P\) \(\displaystyle M=-P(\ell-x)\) |
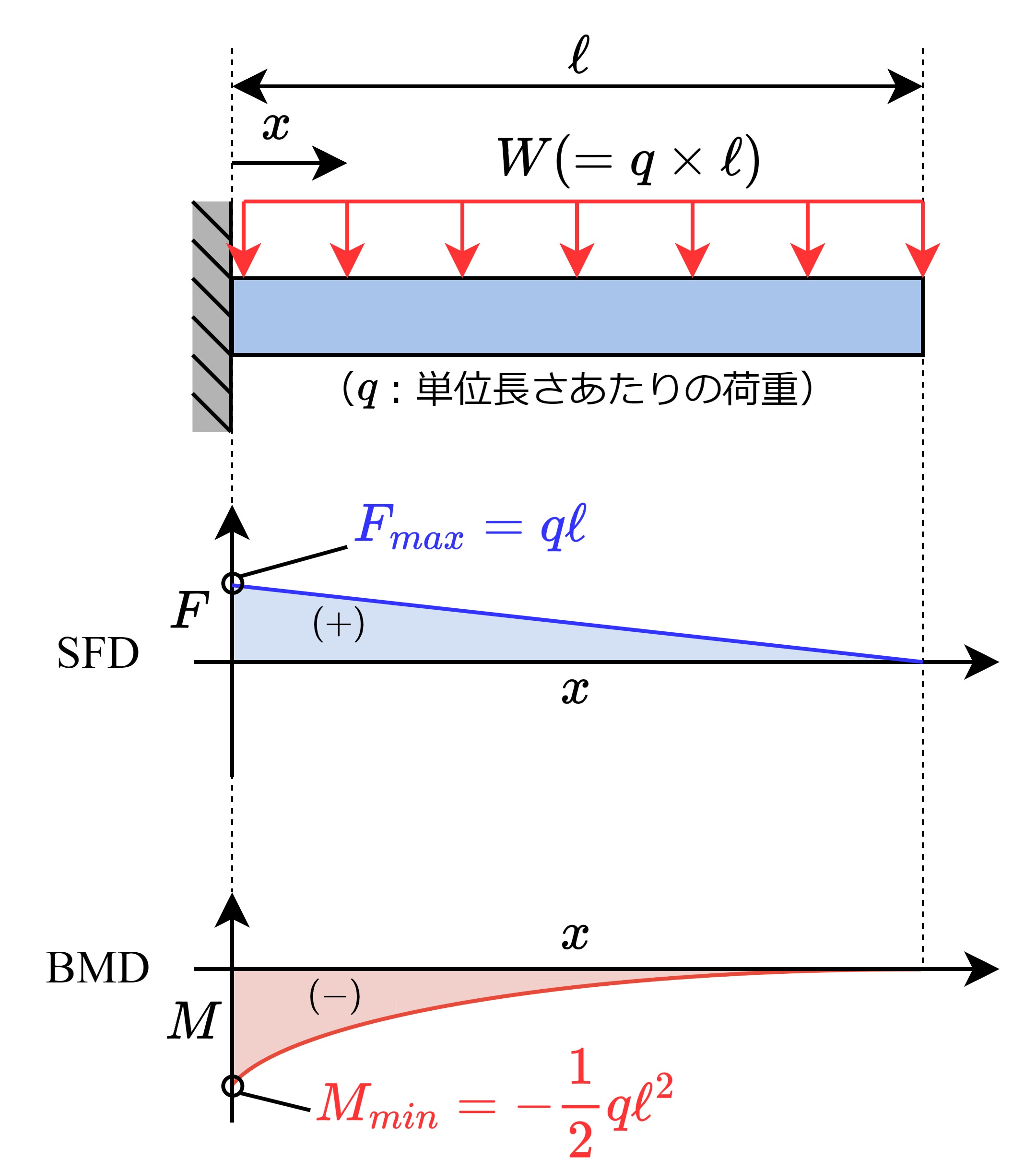 | \(\displaystyle F=q(\ell-x)\) \(\displaystyle M=-\frac{q}{2}(\ell-x)^2\) |
覚えておくべきグラフの特徴（5つ）
せん断力図（SFD）と曲げモーメント図（BMD）の覚えておくべき特徴を５つ挙げます。自分でグラフを書いた時に形がおかしくないかを確認するため、頭に入れておくと良いでしょう。試験等でも役立ちます。
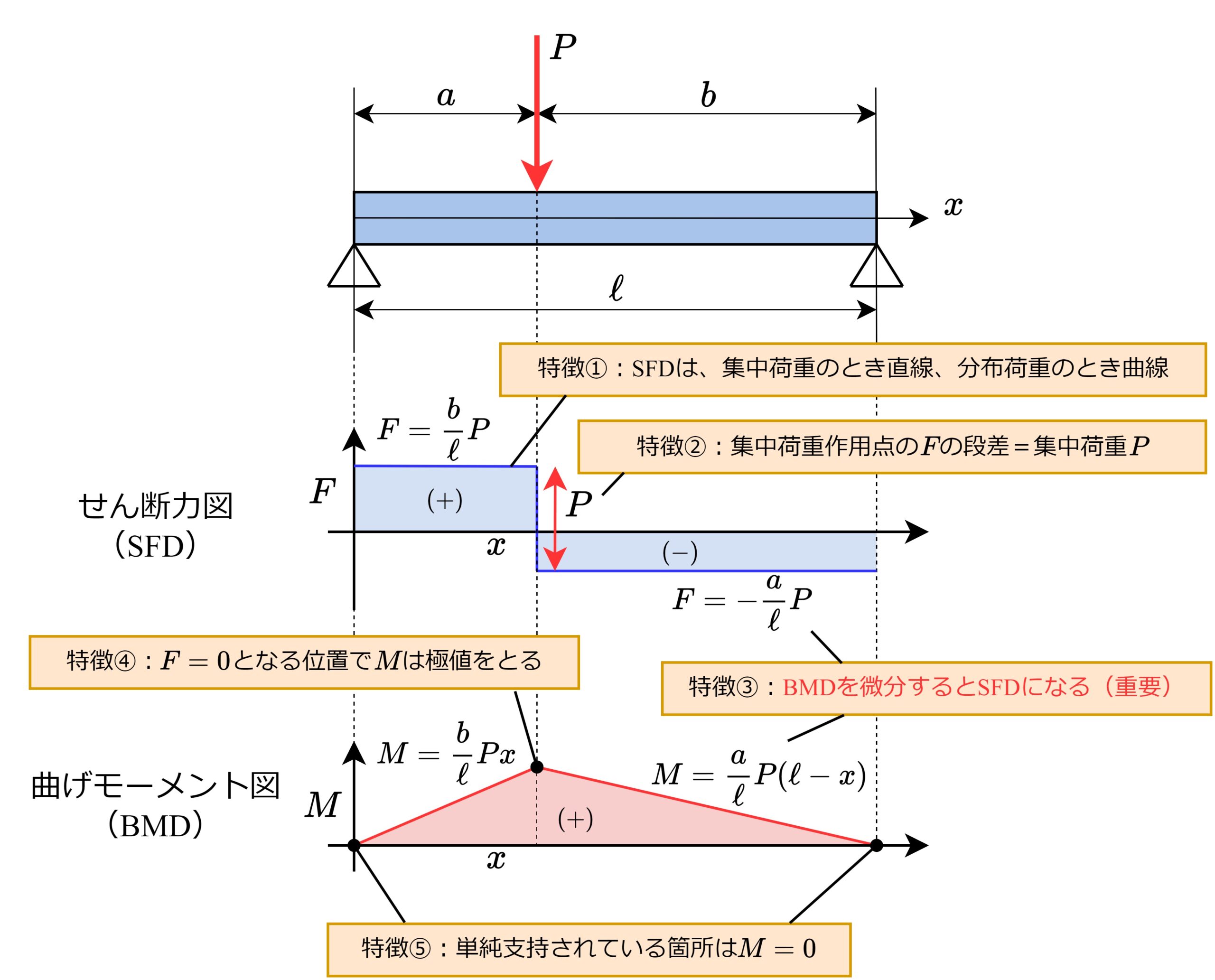
- 【特徴①】せん断力図（SFD）は、集中荷重のとき直線、分布荷重とき曲線
- 【特徴②】集中荷重作用点のせん断力\(F\)の段差＝集中荷重\(P\)
- 【特徴③】曲げモーメント図（BMD）を微分するとせん断力図（SFD）になる
- 【特徴④】せん断力\(F=0\)となる位置で曲げモーメント\(M\)は極値をとる
- 【特徴⑤】単純支持されている箇所は曲げモーメント\(M=0\)
下図を例に、順に解説します。
【特徴①】せん断力図は、集中荷重のとき直線、分布荷重とき曲線
上で紹介したせん断力図の一覧を見て分かる通り、せん断力図は集中荷重のとき直線、分布荷重のとき曲線となります。
【特徴②】集中荷重作用点のせん断力の段差＝集中荷重
集中荷重作用点におけるせん断力\(F\)の段差は、集中荷重\(P\)と同じ値となります。
例えば梁の長手方向の2箇所に\(P_1,P_2\)の荷重がそれぞれ作用していた場合でも、その位置でせん断力図にはそれぞれ\(P_1,P_2\)の段差が生じます。
【特徴③】曲げモーメント図を微分するとせん断力図になる
せん断力図の\(F\)は、曲げモーメント図の\(M\)の傾き（勾配）を表しており、以下の関係があります。
$$\frac{dM}{dx}=F$$
つまり、曲げモーメント図が求まれば、それを\(x\)で微分する事で簡単にせん断力図を描くことが出来ます。自分の描いたグラフが合っているか確認する際に有力な情報となりますので、この特徴は特に覚えておくと良いです。
【特徴④】せん断力＝０となる位置で曲げモーメントは極値をとる
上記の通り曲げモーメント図を微分するとせん断力図となります。従って、せん断力の正負が変わる位置（\(F=0\)となる位置）において、曲げモーメントの勾配の正負が変わる（＝極値をとる）ことになります。
【特徴⑤】単純支持されている箇所は曲げモーメント＝０
単純支持されている箇所は「梁が置いてあるだけ」なので回転を支持できず、曲げモーメントを受ける事がありません。よって単純支持された点において曲げモーメント\(M＝0\)となります。
一方で、壁などで固定支持されている場合は、梁の端でも曲げモーメント\(M\)を受けることが出来ます。
梁はほとんどの場合「曲げモーメント」で壊れる
梁にはせん断力と曲げモーメントが掛かりますが、実はせん断力で梁が壊れることは稀で、ほとんどの場合は曲げモーメントで壊れます。
これは一般的な梁の形状において、曲げ応力の最大値と、せん断応力の最大値を比べた時に、曲げ応力の方が桁違いに大きいからです。試験問題などではせん断力と曲げモーメントの両方を求めますが、実務においては、このような理由でせん断力を計算しない場合もあります。
詳細については、別の記事で詳しく解説しています。
物体内の二つの平面が互いにずれるような変形を「せん断」と言い、この時にかかる力を「せん断力」と言います。機械設計においては曲げや引張と合わせて、せん断についての考慮も欠かせません。 本記事では、せん断力の意味・求め方・許容値など[…]
まとめ
梁の曲げ問題におけるせん断力・曲げモーメントの求め方、およびせん断力図（SFD）・曲げモーメント図（BMD）の描き方について解説しました。
ポイントをまとめます。
- せん断力とは、部材を「互い違い」にずらすような内力のこと。
- 曲げモーメントとは、部材の内部に発生する「断面を回転させるモーメント」のこと。
- せん断力と曲げモーメントは、梁を仮想的に切断して、力とモーメントの釣り合いを解いて求める。
- せん断力図（SFD）と曲げモーメント図（BMD）を描けば、どの位置で最大の力が掛かるかが一目瞭然となる。
- SFDとBMDは、以下の特徴を覚えておくと便利：
①SFDは、集中荷重のとき直線、分布荷重とき曲線
②集中荷重作用点のせん断力\(F\)の段差＝集中荷重\(P\)
③BMDを微分するとSFDになる
④せん断力\(F=0\)となる位置で曲げモーメント\(M\)は極値をとる
⑤単純支持されている箇所は曲げモーメント\(M=0\)
皆様の参考になれば幸いです。
