構造力学や機械設計において頻繁に登場する「曲げモーメント」。
言葉の響きは分かりやすいものの、「どんな力なのか?」「なぜモーメントと呼ぶのか?」といった本質を正しく説明できる人は意外と少ないかもしれません。
本記事では、曲げモーメントの基本的な考え方から、計算方法、代表的な公式までを図や例を交えてわかりやすく解説します。学生・若手エンジニア・構造設計に関わる方に向けて、曖昧な理解をしっかり補強できる内容になっています。
曲げモーメントとは
はじめに、曲げモーメントの定義や、正負のルール、記号・単位、そして他のモーメントとの違いについて整理します。力学が苦手な人でも“感覚”で理解できるよう、順を追って解説していきます。
曲げモーメントとは何か
曲げモーメントとは、部材に外力がかかったとき、その部材を「曲げる方向に働く力のモーメント(回転させる力)」のことです。
もっと正確に言えば、部材の内部に発生する「断面を回転させようとする力」を指します。
このように聞くと少し抽象的ですが、図を見ながらイメージしてみましょう。
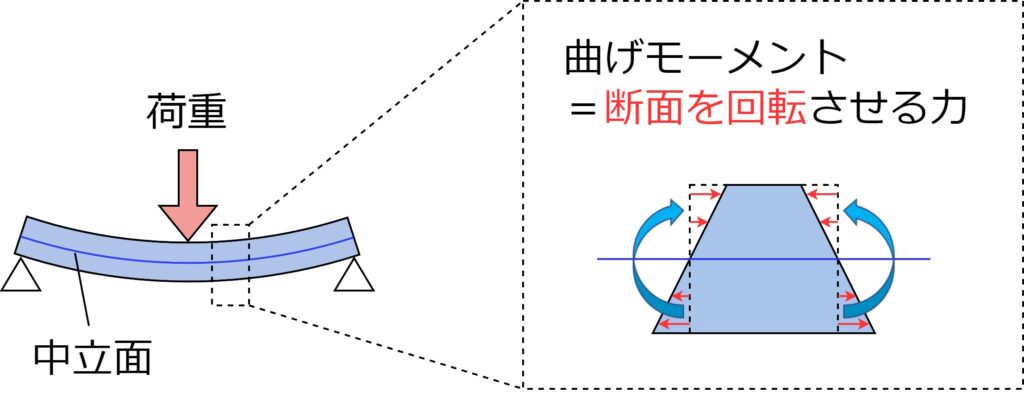
たとえば梁の両端を固定し、中央に荷重をかけたとします。梁全体は弓のようにしなり、上側が圧縮、下側が引張される形で曲がっていきます。このとき、梁の内部では各断面がわずかに回転するような力を受けており、それこそが「曲げモーメント」なのです。
つまり、曲げモーメントとは「梁を単に押しつぶす・引っぱる」のではなく、「回転させて変形させる」内部の力。この内部の回転力をモーメント(力 × 距離)という形で数値化し、部材の安全性や変形量を評価していきます。
曲げモーメントの正負
曲げモーメントには正負の方向にお約束があり、「下側に凸となる場合に曲げモーメントを正とする」という考えが一般的です。
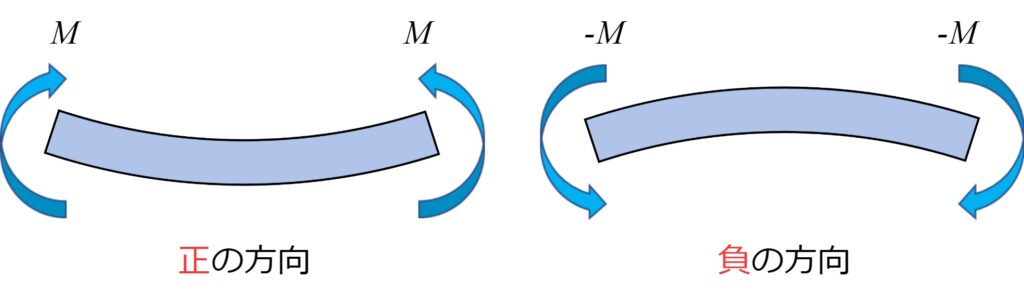
覚え方としては、最も基本的な梁であるな単純梁(両端支持梁)の場合に、重力などで自然に曲がる方向を正とする、と考えるとよいでしょう。
現実世界では梁に掛かる荷重は下向き(重力の方向)となる場合がほとんどなので、この向きを正としておく方が便利、という事です。
曲げモーメントの記号・単位
曲げモーメントは記号\(M\)で表します。
曲げモーメントも「力のモーメント」と同様に力×距離で計算するので、単位は[Nm]です。
計算方法の詳細については後述します。
力のモーメントとの違い
「曲げモーメント」と「力のモーメント」は別物です。
一言でいうと、力のモーメントは外力、曲げモーメントは内力という違いがあります。
力のモーメントは「外力による物体全体の回転」を考えるのに対し、曲げモーメントは「外力を受けた物体内部の断面の回転」を考えます。
曲げモーメントの求め方
上で説明したように曲げモーメントは「断面を回転させる力」です。
ある断面における曲げモーメントを知るには、梁を仮想的に切り断面を出現させ、「この断面に曲げモーメントがいくら掛かると考えれば、切り離した梁におけるモーメントのつり合いが取れるか」を考えて算出します。
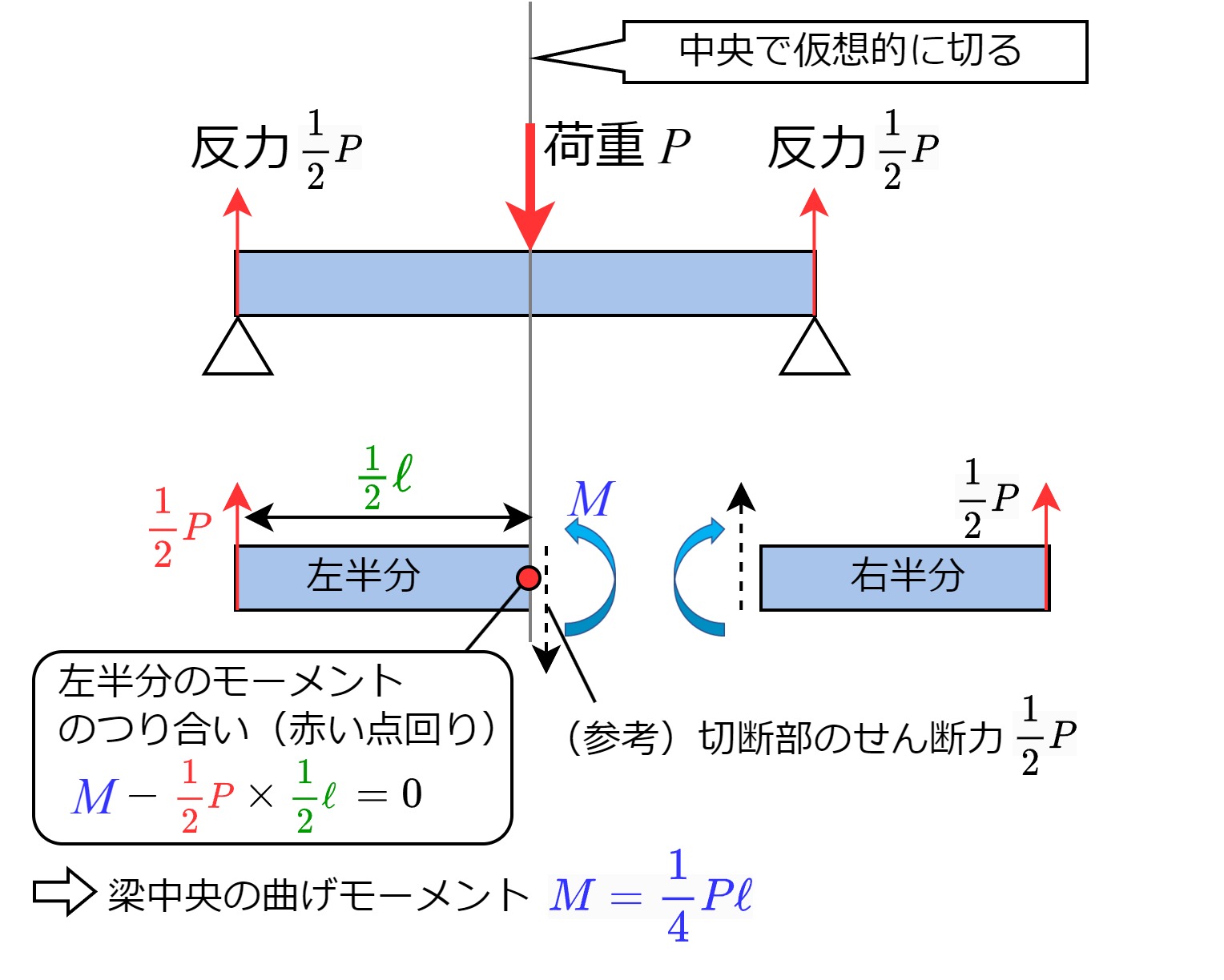
算出した曲げモーメントを、見易いようにグラフ化したものが曲げモーメント図(BMD)です。
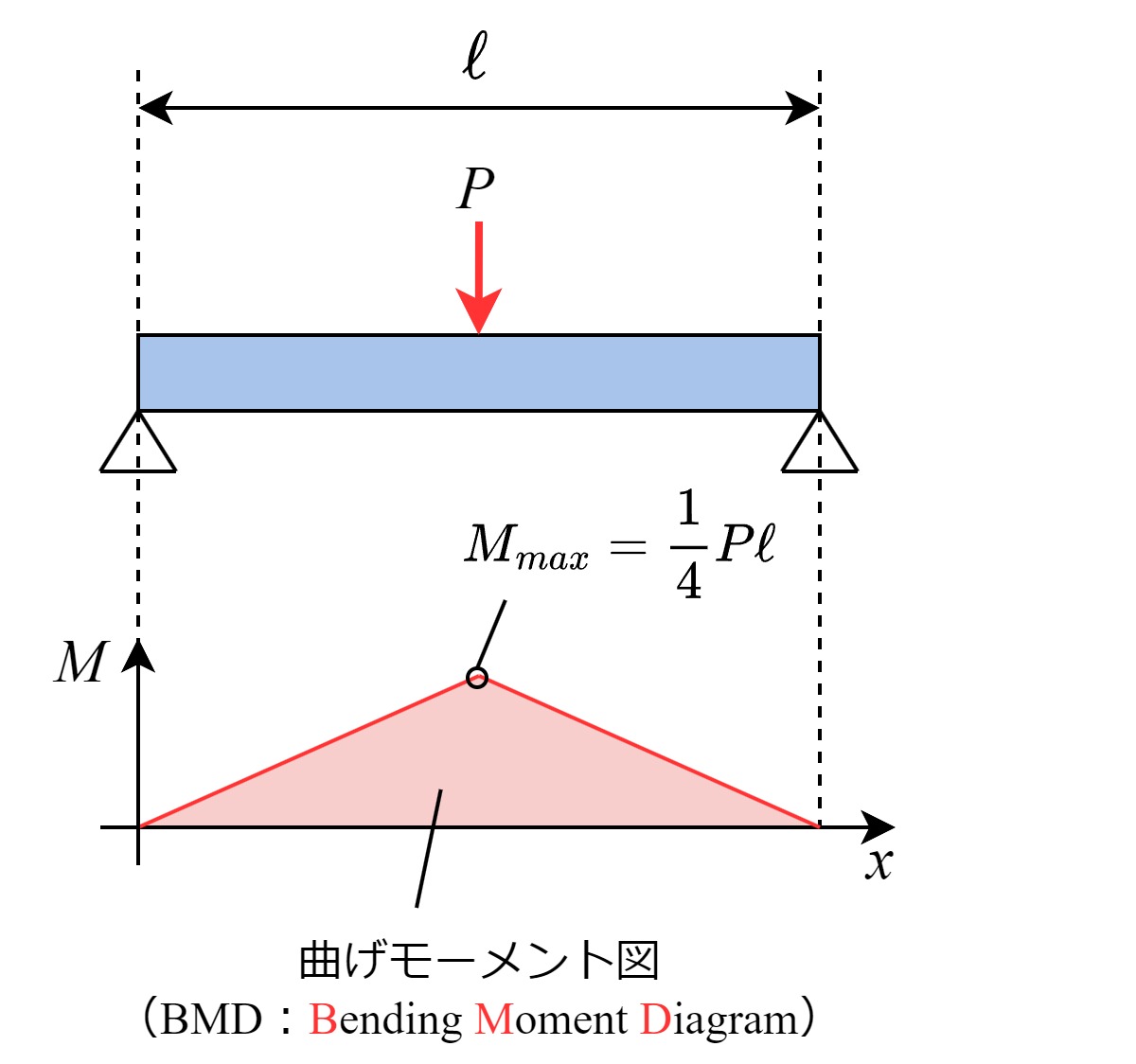
曲げモーメントの計算方法の詳細と、曲げモーメント図の描き方については、別記事で詳しく解説しています。
梁の曲げ問題ではせん断力と曲げモーメントを求め、その分布をグラフにした「せん断力図」と「曲げモーメント図」を作成します。 本記事では、せん断力図と曲げモーメント図の描き方と、試験等でも役立つ「覚えておくべきグラフの特徴5つ」を解説し[…]
なお、本記事では割愛しましたが、梁には曲げモーメントの他に「せん断力」も働きます。曲げモーメントとせん断力はセットで考える事が重要です。せん断力については別の記事で詳しく解説しています。
物体内の二つの平面が互いにずれるような変形を「せん断」と言い、この時にかかる力を「せん断力」と言います。機械設計においては曲げや引張と合わせて、せん断についての考慮も欠かせません。 本記事では、せん断力の意味・求め方・許容値など[…]
曲げモーメントの公式
代表的な梁における曲げモーメント図(BMD)と、曲げモーメントの公式を一覧で示します。
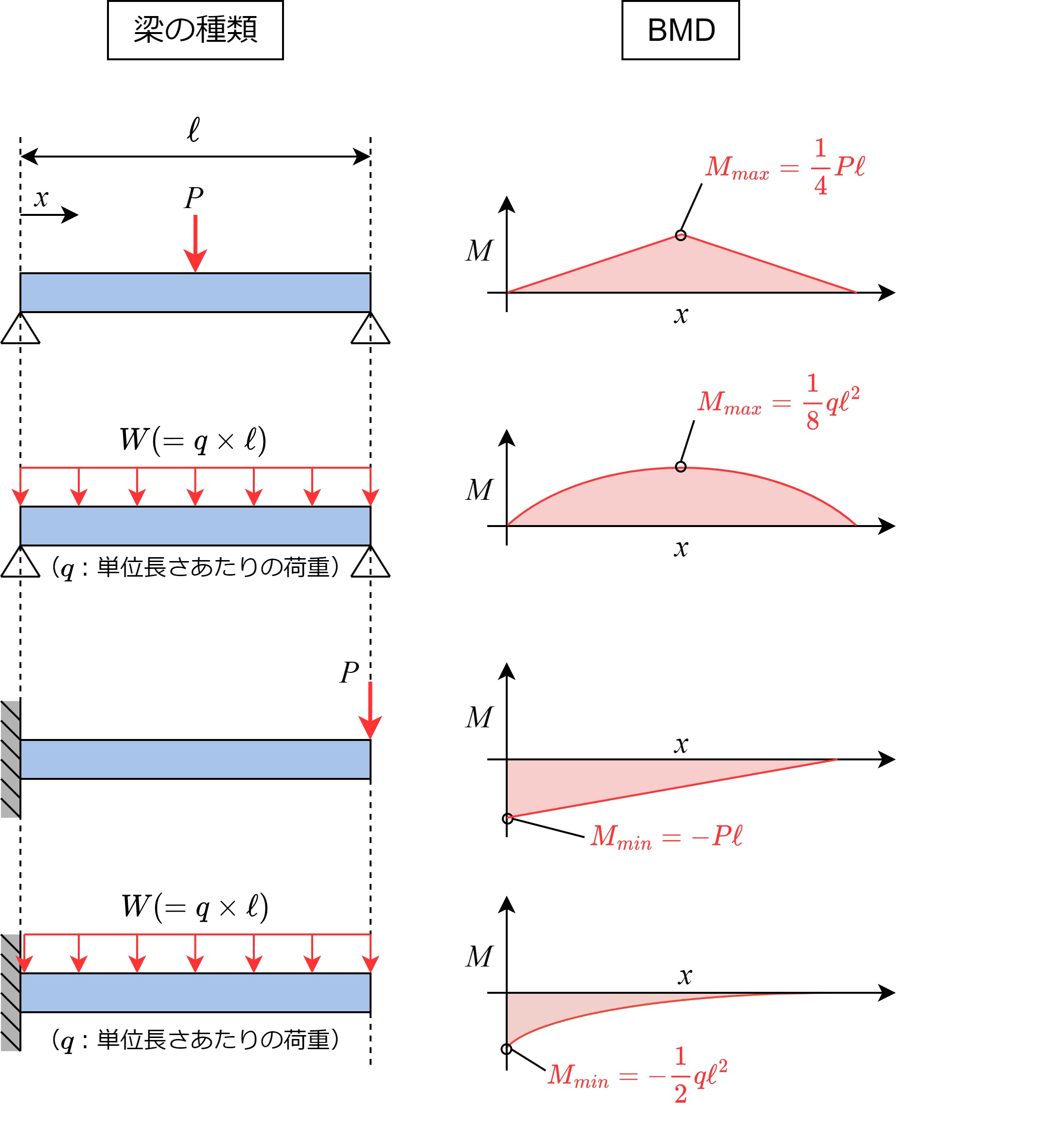
曲げモーメント図(BMD)の描き方と公式の詳細については別の記事で解説していますので、気になる方は下記からご覧ください。
👉【保存版】曲げモーメント図・せん断力図の描き方と覚えておくべき5つの特徴
なお、上の図で紹介したのは基本的なケースのみです。荷重条件がより複雑な場合の曲げモーメントの公式一覧や導出方法を知りたい方は、下記の書籍が役立ちます。
おすすめポイント
- 材料力学を基礎からしっかり学べる定番書
- 図解が豊富で独学でも理解しやすい
- 資格試験・実務のどちらにも活用できる
運営者自身も10年以上使い続けており、今でも設計や資格勉強の際に必ず開く本です。
曲げ応力との関係
「曲げモーメント」と「曲げ応力」は、名前が似ていますが別物です。
| 曲げモーメント | 部材を曲げようとする力(断面を回転させる力) |
| 曲げ応力 | 部材の内部に発生する引張・圧縮応力 |
両者の関係を説明します。
下図のように曲げられた梁の微小部分を切り出したとき、断面には赤矢印のイメージで曲げ応力\(\sigma\)がかかります。曲げ応力の掛かり方の特徴は以下の通りです。
- 中立面を境に、凹側(上側)は圧縮、凸側(下側)は引張りとなる
- 中立面から遠くなるほど曲げ応力が大きくなり、表面で最大となる
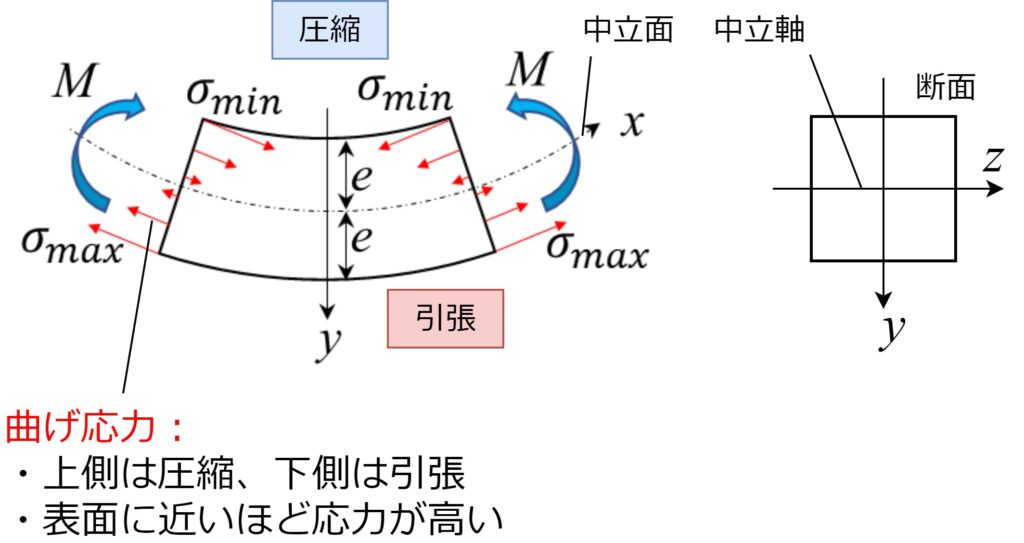
このとき、曲げモーメント\(M\)と、曲げ応力\(\sigma\)の関係は次のように表されます。
$$\sigma=\frac{My}{I} \tag{1} $$
- \(\sigma\):曲げ応力
- \(M\):曲げモーメント
- \(y\):中立軸までの距離
- \(I\):断面二次モーメント
なお断面二次モーメント\(I\)とは、部材の変形しにくさを表す物理量で、断面形状によって算出されるものです。詳しくは別記事で解説しています。
「断面二次モーメント」という言葉を聞いて、ピンとこない方もいるかもしれません。材料力学や構造設計において頻繁に登場するこの概念は、梁や柱の設計において非常に重要な役割を果たします。 しかし、その専門的な響きから、理解が難しいと感[…]
さて、式(1)より曲げモーメントが大きい場所ほど曲げ応力も大きくなり、こうした場所で部材が壊れやすくなる、という事が分かります。
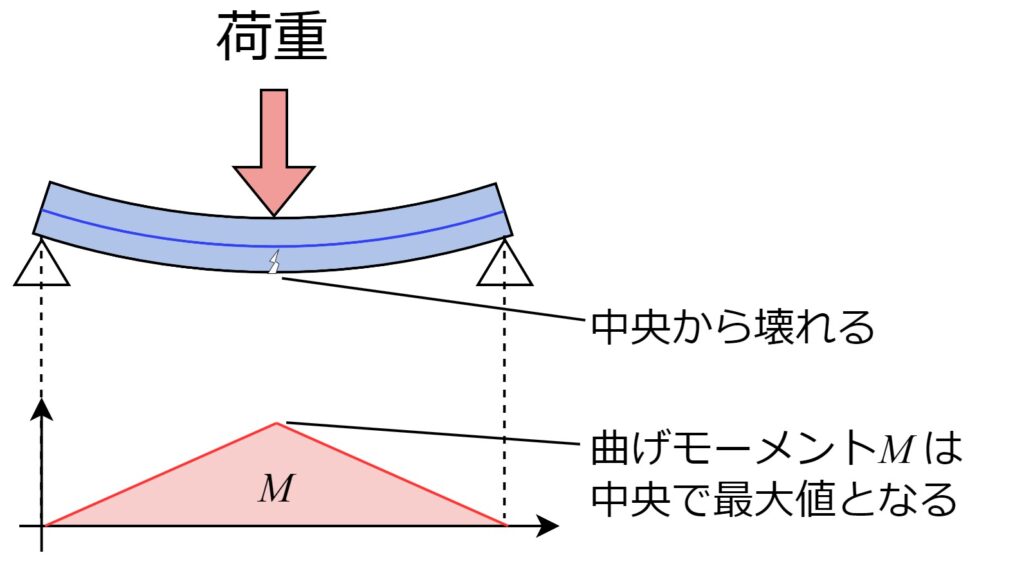
例えば下図の場合、荷重を増やしていくと中央で梁が折れる事がイメージできると思います。
これは曲げモーメントが中央の位置で最大となるため、曲げ応力も中央で最大となるからです。なお梁の上側は圧縮、下側は引張となりますので、梁中央の下側から引張応力によって引きちぎられるように梁が破断していきます。
曲げモーメントによる変形(たわみ)
曲げモーメントが分かれば、梁の変形量(たわみ)を求める事ができます。
下の図のように断面二次モーメント\(I\)、ヤング率\(E\)の梁に曲げモーメント\(M\)を掛けたとき、梁の中立面における曲率\(1/\rho\)は次のように表されます。
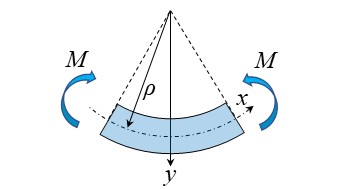
\( \frac{1}{\rho}=\frac{M}{EI}=-\frac{d^2y}{dx^2} \)
梁の固定方法から決まる境界条件を与えて微分方程式を解くと、たわみ量を計算する事ができます。(詳細は省きます)
例えば下の図のように、長さ\(\ell\)の片持ちはりの先端に集中荷重\(P\)が掛かる場合、先端のたわみ\(y\)は次のようになります。

\(y=\frac{P\ell^3}{3EI}\)
このように、曲げモーメントから梁のたわみを求める事ができます。
梁のたわみの求め方・公式の覚え方については、以下の記事で詳しく解説しています。
梁に荷重が加わったとき、梁が変形する量を「たわみ」と言います。 本記事では、材料力学におけるたわみの求め方、試験等で役立つ公式の覚え方をわかりやすく解説します。 たわみとは 「たわみ」とは何か たわみとは、梁に[…]
また、たわみの公式の導出方法については、以下の記事で詳しく解説しています。
梁に荷重が加わった時の変形量を「たわみ」と言います。たわみの大きさは公式を使えば簡単に計算する事ができますが、本記事では公式の導出方法・考え方を図解で分かりやすく解説します。 導出の流れを頭に入れておくと、試験で公式を忘れてしまった[…]
まとめ
曲げモーメントとは
曲げモーメントの考え方・計算方法・公式について解説しました。
ポイントをまとめます。
- 曲げモーメント(部材を曲げようとする力)は、断面を回転させる力で表現する
- 曲げモーメントは下側に凸変形する方向を正、上側に凸変形する方向を負とする
- 曲げモーメントが大きい箇所では曲げ応力が大きくなり、部材が壊れやすい
- 曲げモーメントを計算するには、梁を仮想的に切断し断面を出現させ、切り離した梁におけるモーメントのつり合いを考える
皆様の参考になれば幸いです。
参考文献
本記事の解説は下記の書籍を参考にしています。材料力学を基礎からしっかり学びたい方に、もっとも信頼できる一冊です。図解が豊富で独学でも理解しやすく、資格試験・実務どちらにも活用できます。運営者も10年以上使い続けており、今でも実務や資格勉強の際に必ず開く本です。ぜひ下記からチェックしてみてください。







