流体力学や配管設計では「レイノルズ数」が頻繁に登場します。
本記事ではレイノルズ数の求め方・物理的な意味を解説していきます。
レイノルズ数とは何か
レイノルズ数とは流れの状態を知る上で重要な数値であり、
「流体の粘性力と慣性力の比」で定義される無次元量です。
無次元量なのでレイノルズ数には単位がありません。
主に、流れが層流か乱流かを見分けるために使われます。
「粘性力と慣性力の比」の意味や「層流と乱流」については後述します。
レイノルズ数の求め方
定義式
レイノルズ数は以下の定義式で求めます。
$$Re=\frac{\rho V L}{\mu}=\frac{VL}{\nu}$$
- \(\rho\):流体の密度 \(\rm{(kg/m^3)}\)
- \(V\):流体の速度 \(\rm{(m/s)}\)
- \(L\):代表長さ \(\rm{(m)}\)
- \(\mu\):流体の粘度 \(\rm{(Pa・s)}\)
- \(\nu\):流体の動粘度 \(\rm{(m^2/s)}\)
代表長さとは
「代表長さ」という言葉通り、流れの形を代表していれば、
基本的にはどのように取っても構いません。
ただし配管の場合は内径、自動車の場合は車高、飛行機の翼の場合は翼弦、
のように、対象物によって代表長さ\(L\)の取り方の「お約束」があります。
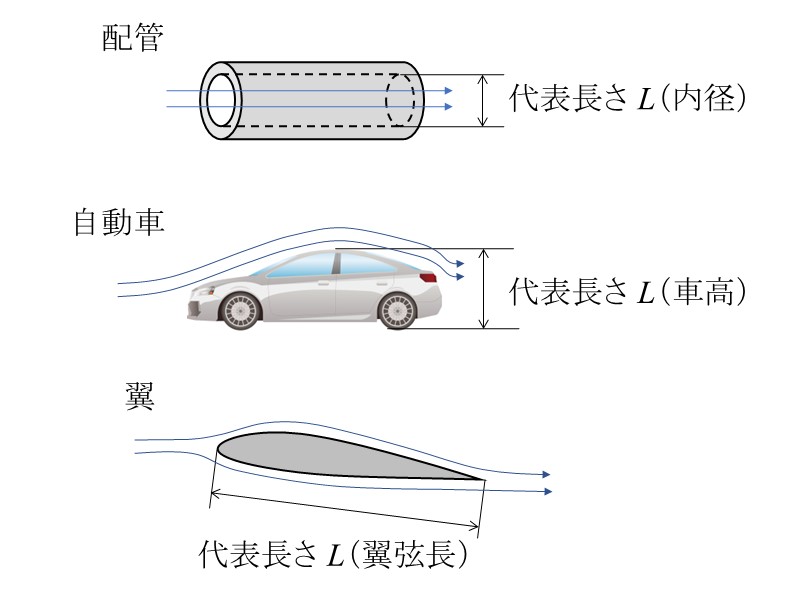
レイノルズ数は流れを相似形状で捉えて比較するものなので、
正しく比較するためには、対象物ごとに代表長さ\(L\)の取り方を揃える必要があります。
粘度、動粘度とは
粘度\(\mu\)は流体の「さらさら」「ドロドロ」具合を表す物性値です。
一方、動粘度\(\nu\)は「流れの伝わりにくさ」を表す物性値で、
粘度\(\mu\)を密度\(\rho\)で割って求めます。
$$\nu=\frac{\mu}{\rho}$$
粘度と動粘度の定義・違い・直感的なイメージについては、
以下の記事で詳しく解説しています。
流体の物性値として「粘度」と「動粘度」があります。 定義が分かり難く、名前も似ているため取っ付き難いイメージがあるかと思います。 本記事では「粘度」と「動粘度」の定義・計算方法・両者の違いを詳しく解説します。 粘度([…]
レイノルズ数は「粘性力と慣性力の比」を表す
レイノルズ数は「分母が流体の粘性力」、「分子が流体の慣性力」を表しており、
全体で「粘性力と慣性力の比」を表しています。
流れを下の図のようにモデル化したとき、
粘性力と慣性力どのように表せるかを考えます。
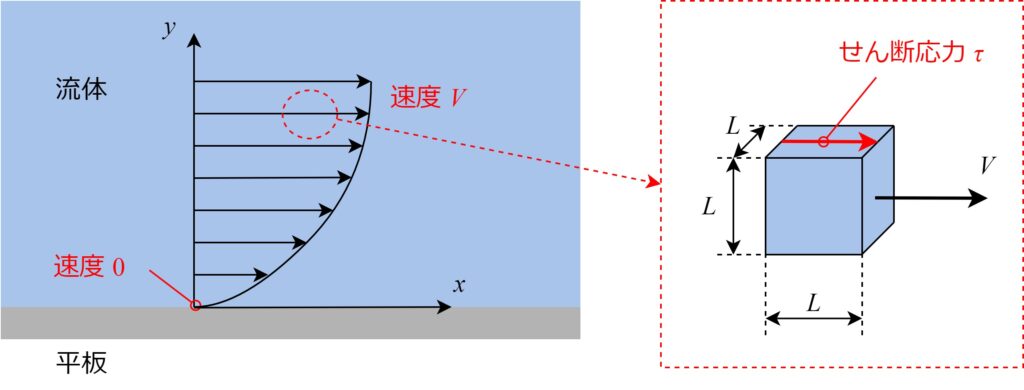
粘性力
粘性力は流体に作用するせん断応力\(\tau\)に起因します。
ニュートンの粘性法則より、せん断応力\(\tau\)は以下で表されます。
$$\tau=\mu\frac{dV}{dL}$$
(上式は粘度\(\mu\)の定義式としてよく使われます。)
これに流体の断面積\(L^2\)を掛ければせん断力になりますから、
流体に作用する粘性力\(F_v\)は以下のようになります。
$$F_v=(面積)×(せん断応力)=L^2×\mu\frac{dV}{dL}$$
慣性力
流体の加速度\(\alpha\)は、速度\(V\)の時間(\(t\))変化として以下で表されます。
$$\alpha=\frac{dV}{dt}$$
これに質量\(\rho L^3\)を掛ければ力になりますから、
流体に作用する慣性力\(F_i\)は以下のようになります。
$$F_i=(質量)×(加速度)=\rho L^3×\frac{dV}{dt}$$
慣性力/粘性力がレイノルズ数となる
上で求めた粘性力と慣性力の比を取り、速度\(V=dL/dt\)を考慮すると、
レイノルズ数の定義式になる事が確認できます。
$$Re=\frac{慣性力}{粘性力}=\frac{\rho L^3×\frac{dV}{dt}}{L^2×\mu\frac{dV}{dL}}=\frac{\rho L \frac{dL}{dt}}{\mu} =\frac{\rho V L}{\mu}$$
レイノルズ数で層流 or 乱流を判定できる
レイノルズ数の大小によって流れが「層流」か「乱流」かが決まります。
層流とは
目安として\(Re<2,300\)の時、流れは層流となります。
層流とは流れが乱れることなく、整列しながら真っすぐ進んでいる状態です。
レイノルズ数は慣性力/粘性力ですので、流体の粘性力が強い場合、
流れが自由に動き回ろうとする力が抑えられるので、
層流になり易くなります。
乱流とは
目安として\(Re>4,000\)の時、流れは乱流となります。
乱流とは流れが様々な方向に乱れた状態です。
レイノルズ数は慣性力/粘性力ですので、流体の慣性力が強い場合、
流れが自由に動きまわる力が粘性力に勝ち、乱流になり易くなります。
遷移域とは
\(2,300≦Re≦4,000\)の時は「遷移域」と呼ばれ、
流れの状態により層流になったり、乱流になったりします。
層流・乱流の比較
レイノルズ数の違いによる流れの状態を比較します。
| 層流 | 遷移域 | 乱流 | |
|---|---|---|---|
| \(Re\) | \(Re<2,300\) | \(2,300≦Re≦4,000\) | \(Re>4,000\) |
| 流れの様子 |  整列した状態 | 流れの状態により、 層流 or 乱流になる | 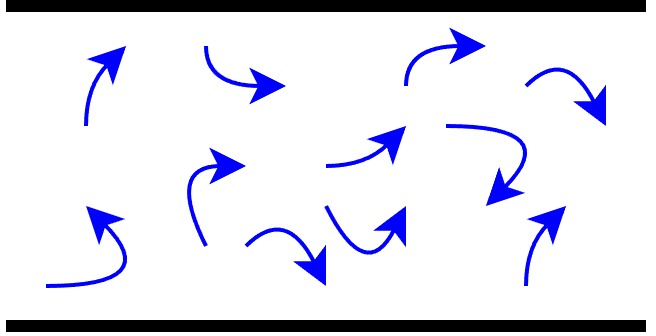 乱れた状態 |
| 速度分布 | 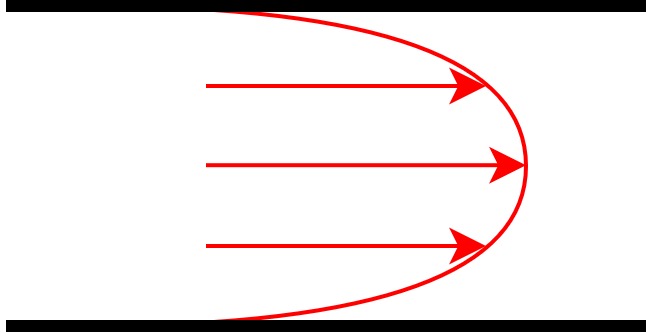 速度ムラが大きい (中央が速い) | 流れの状態により、 層流 or 乱流になる | 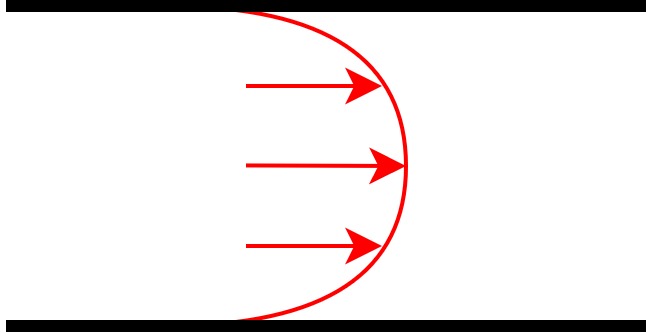 速度ムラが小さい (平均化される) |
ちなみに、実務でレイノルズ数を計算する際、ほとんどの場合は「乱流」となります。
例として以下の条件でレイノルズ数を計算してみます。
- 対象:水配管
- 流速\(V\):\(1.5\rm{m/s}\)(標準流速)
- 管径\(L\):\(50\rm{mm}\)
- 動粘度\(\nu\):\(1.004×10^{−6} \rm{m^2/s}\) (20℃)
$$Re=\frac{VL}{\nu}=\frac{1.5×0.05}{1.004×10^{−6}}=74,701$$
配管設計において全く特殊な条件ではありませんが、
「\(Re>4,000\)」の閾値の19倍もの値であり、
乱流であることが確認できます。
【※注意】なお、今回は配管の流れにおけるレイノルズ数の閾値を示しています。
上で述べたたように、流れの対象物によって代表長さ\(L\)が異なるので、
対象物が変わればレイノルズ数の閾値も変わります。
レイノルズの相似則
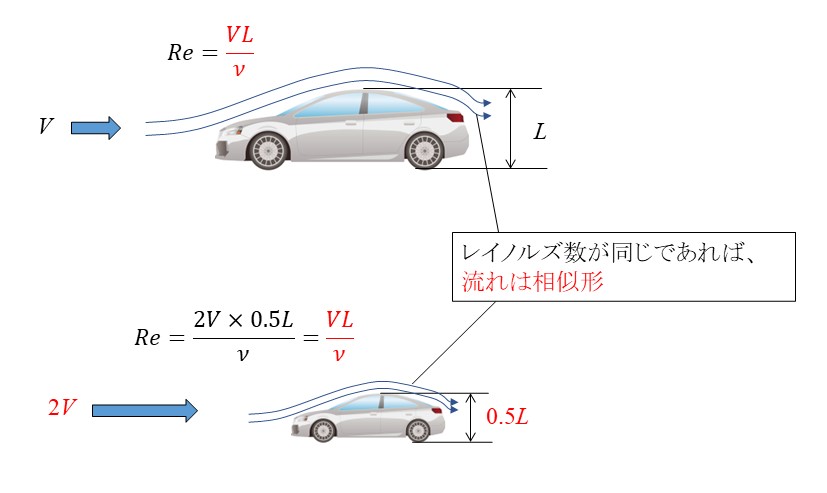
レイノルズの相似則とは、
「レイノルズ数が同一であれば、流れの様子は相似形になる」
という法則です。
車や飛行機などの大きい物体の場合、
実物大で実験すると大掛かりな装置が必要になり大変です。
レイノルズの相似則を使う事で、
小さな模型でも実物と同じ流れを再現する事が可能になり、
実験の効率が向上します。
【※注意】なお、マッハ数が0.3を超える場合は圧縮性の影響を無視できなくなるので、
相似性を保つためにはレイノルズ数とマッハ数の両方を合わせる必要があります。
まとめ
レイノルズ数の求め方と物理的な意味を解説しました。
ポイントをまとめます。
- レイノルズ数は流れの様相を決める無次元量である
- レイノルズ数は慣性力/粘性力で定義され、公式は\(Re=VL/\nu\)
- レイノルズ数が小さいと層流、大きいと乱流になる
- レイノルズ数が同一であれば、スケールは違っても流れは同じ(相似形)になる
皆様の参考になれば幸いです。






