梁の曲げを考える際、「断面係数」という物理量が登場します。
本記事では断面係数の意味・求め方を初学者でも分かるよう、図解を交えて詳しく解説します。
「断面係数」とは何か？
何を表しているのか
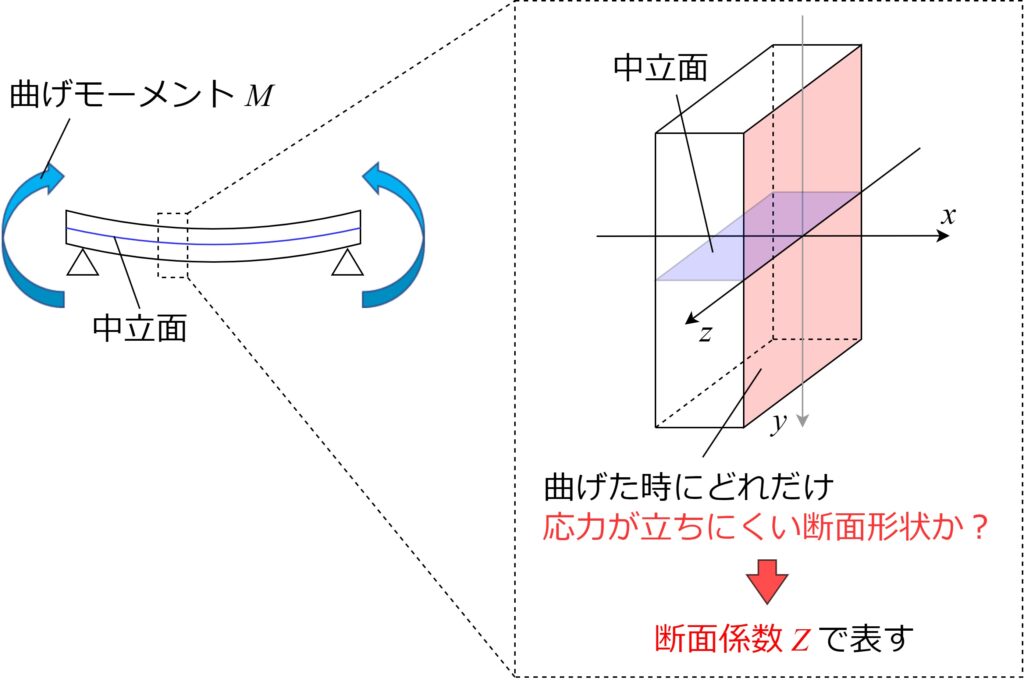
「断面係数」とはズバリ、「曲げた時にどれだけ応力が立ちにくい（強い）断面形状か」を表す物理量です。
梁にかかる応力を求める際に必要で、材質などは関係せず、形状・寸法のみによって決まります。断面係数が大きいほど応力が立ちにくく、破断しにくい（強い）断面形状である事を意味します。
なお、はりの曲げ・曲げモーメントについては、別の記事で詳しく解説しています。
梁の曲げを考える際には「曲げモーメント」が登場します。 言葉の分かりやすさから、理解した気になりやすい曲げモーメント。 本記事では、そんな曲げモーメントの考え方・計算方法・公式について一からわかりやすく解説します。 […]
名前が似ている「断面二次モーメント」との違い
断面係数と良く似たものに「断面二次モーメント」がありますが、別の物理量ですので混同しないように注意しましょう。
断面係数は「梁に掛かる応力」を求める際に使うのに対し、
断面二次モーメントは「梁のたわみ・変形量」を求める際に使います。
計算に便利なように、式のまとめ方（定義）が少し違います。
断面二次モーメントの意味・求め方については別の記事で詳しく解説しています。
梁の曲げを考える際には「断面二次モーメント」が登場します。 材料力学で習いますが名前からして取っつき難く、公式は知っているが良く分からないモノ、という印象があるかと思います。 本記事では断面二次モーメントとは何か、どんな意[…]
「断面係数」と「断面二次モーメント」は混同しやすいため、両者の違いについても別の記事で詳しく解説しています。
材料力学では「断面二次モーメント」と「断面係数」が頻出しますが、名前も算出方法も似ているので混同し易いかと思います。 本記事では断面二次モーメントと断面係数の違いを分かり易く解説します。 断面二次モーメントと断面係数の違い[…]
断面係数の求め方
断面係数は「断面二次モーメント÷中立軸までの距離」で求める
先ほど述べた通り、断面係数とは「曲げた時にどれだけ応力が立ちにくい（強い）断面形状か」を表します。この断面係数は、断面二次モーメントを少し加工して生まれる物ですので、先に断面二次モーメントについて触れておく必要があります。
下図のような曲げモーメント\(M\)がかかる梁の微小部分について考えます。断面には赤矢印のイメージで曲げ応力\(\sigma\)がかかり、凸側（下側）は引っ張られ、凹側（上側）は圧縮となります。曲げ応力の大きさは中立軸から遠くなるほど大きくなり、表面で最大となります。
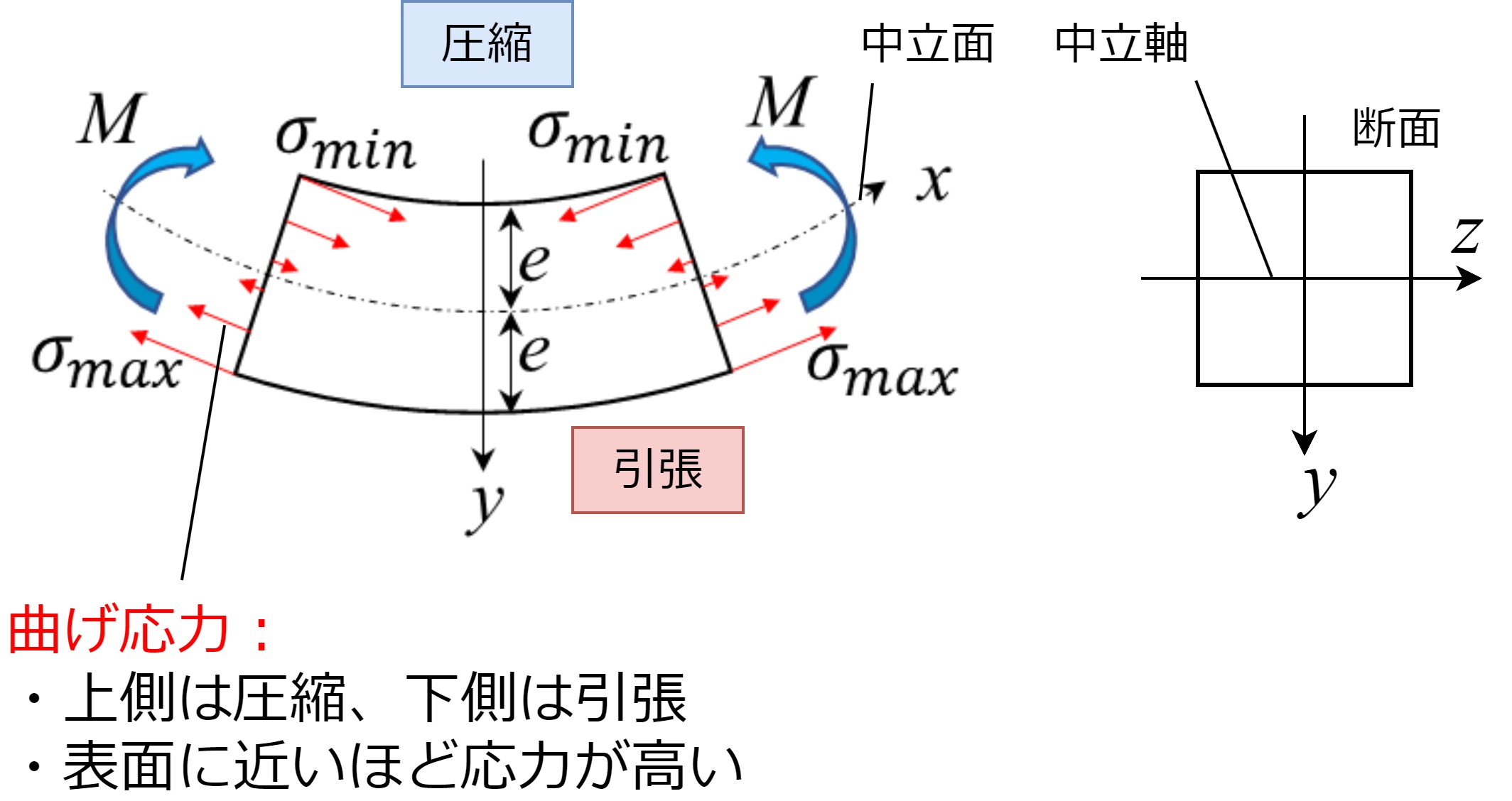
この曲げ応力\(\sigma\)を式で表すと次のようになります。
$$\sigma=\frac{My}{I}$$
- \(\sigma\)：曲げ応力
- \(M\)：曲げモーメント
- \(y\)：中立軸からの距離
- \(I\)：断面二次モーメント
式の導出方法については別の記事で解説予定です。（作成中）
断面二次モーメント\(I\)については上でも軽く述べましたが、詳細は別の記事で解説しています。
梁の曲げを考える際には「断面二次モーメント」が登場します。 材料力学で習いますが名前からして取っつき難く、公式は知っているが良く分からないモノ、という印象があるかと思います。 本記事では断面二次モーメントとは何か、どんな意[…]
上の式を使えば、任意の「中立軸からの距離\(y\)」の位置における曲げ応力を知ることができます。しかし実際の設計においては「最も曲げ応力の高い表面で、応力値（\(\sigma_{max}\)）はいくらか」が重要であり、この値が許容値以下となるかを一番気にします。
つまり梁の表面\(y=e\)における最大の曲げ応力\(\sigma_{max}\)さえ分かれば、内部の応力はどうでもいいのです。
\(\sigma_{max}\)は次のように書けます。
$$\sigma_{max}=\frac{Me}{I}=\frac{M}{I/e}=\frac{M}{Z}$$
ただし、
$$Z=\frac{I}{e}$$
- \(Z\)：断面係数
- \(I\)：断面二次モーメント
- \(e\)：中立軸から梁表面までの距離（上下対象な断面形状の場合は梁の高さの半分）
これが断面係数\(Z\)の定義です。断面二次モーメント\(I\)をあらかじめ\(e\)で割った物理量を定義する事で、\(\sigma_{max}\)の計算式が若干シンプルに書き換えられています。
なぜ「中立軸までの距離」で割るのか
断面二次モーメント\(I\)を計算する際には断面形状は分かっているので、表面～中立軸までの距離\(e\)も当然判明しており、断面係数\(Z\)も計算できる状態になっています。
従って最大の曲げ応力\(\sigma_{max}\)を求める際には、最初から断面係数\(Z\)を使う方が計算の手間が少し減るので、断面係数\(I\)と、それを距離\(e\)で割っただけの断面係数\(Z\)の２つ存在するのです。
よく使う断面係数の公式
円形と長方形の断面係数の公式を示します。よく使う公式なので覚えておくと便利です。
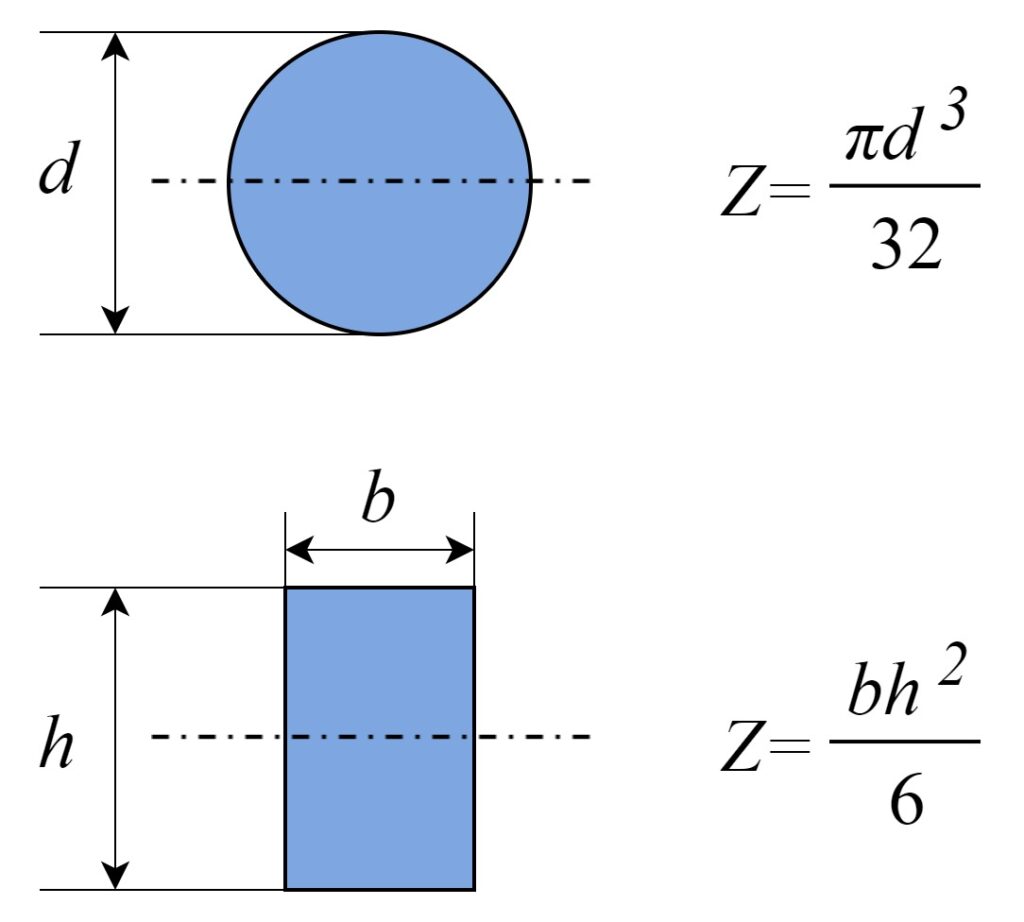
長方形の断面係数を見ると、\(Z\)は幅\(b\)の1乗、高さ\(h\)の2乗に比例して大きくなっています。
従って「部材の曲げ応力を下げたい時は幅\(b\)よりも、高さ\(h\)を大きくした方が効果的」という事が分かります。設計において重要な考え方なので頭に入れておきましょう。
複雑形状の断面係数の求め方
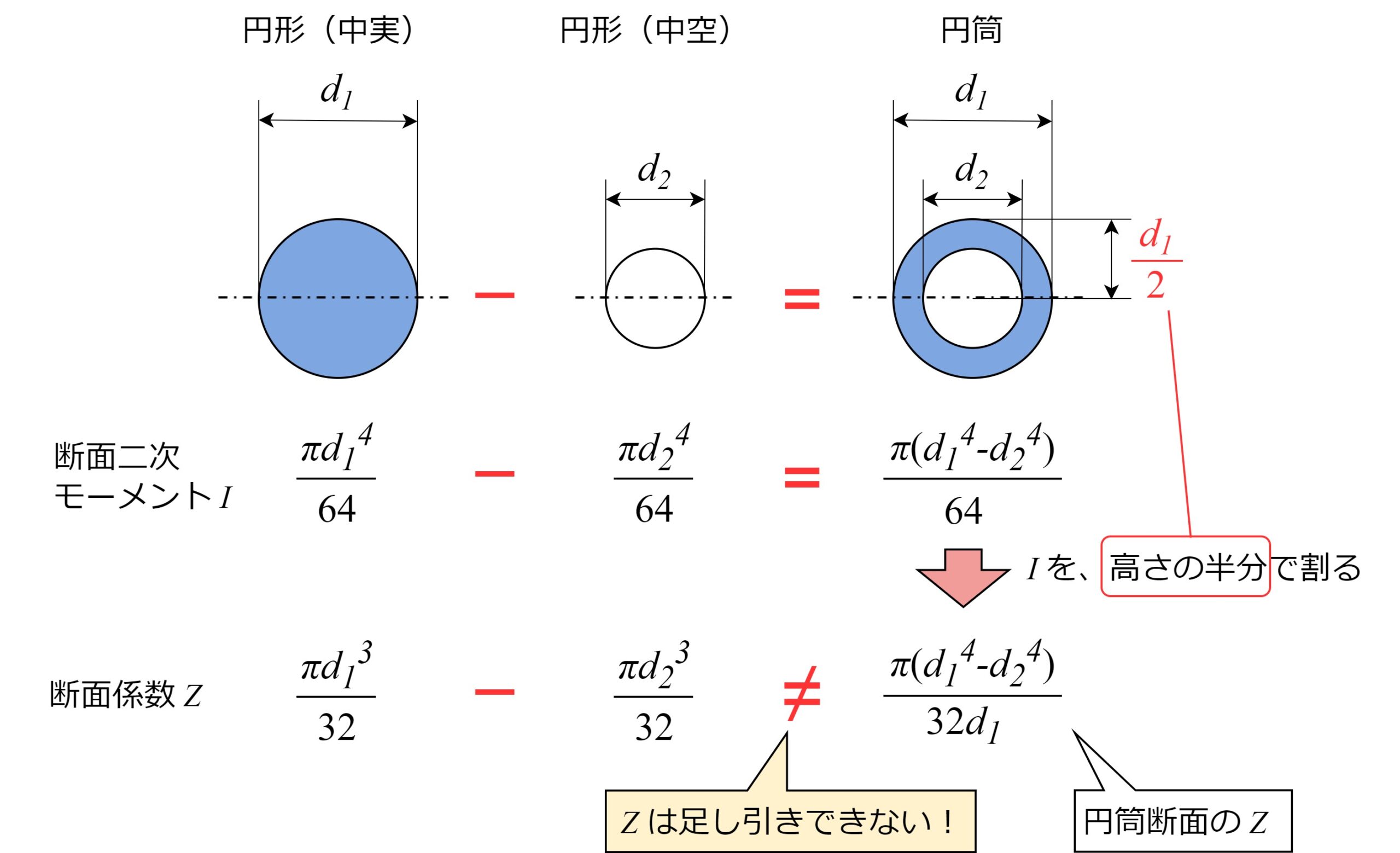
断面係数は単純に「足し引き」できないため、例えば円筒形の断面係数を求める際に「中実円形の断面係数から中抜きされた分の断面係数を引く」という計算はできません。
一方で、断面二次モーメントは「足し引き」できます。複雑形状の断面係数を求める場合は、断面二次モーメントで足し引きした後、断面の高さの半分（表面～中立軸の距離）で割る、というステップで計算できます。
例えば下の図のような円筒形の断面係数を求める際は、
- 中実円形と中空円形の断面二次モーメント\(I\)をそれぞれ求める
- （中実円形）-（中空円形）により、円筒形の断面二次モーメント\(I\)を求める
- これを断面の高さの半分で割って、円筒形の断面係数\(Z\)を求める
というステップで計算する事ができます。
まとめ
断面係数\(Z\)の意味・求め方について詳しく解説しました。
本記事のポイントをまとめます。
- 断面係数は「曲げた時にどれだけ応力が立ちにくい（強い）断面形状か」を表す
- 断面係数を使えば、曲げた梁にかかる最大の曲げ応力を計算できる
- 断面係数は「断面二次モーメント」÷「断面の高さの半分」で求める
- 複雑形状の断面係数は、まず断面二次モーメントで形状の足し引きをした後、それを断面の高さの半分で割る事で求められる
皆様の参考になれば幸いです。
