物体内の二つの平面が互いにずれるような変形を「せん断」と言い、この時にかかる力を「せん断力」と言います。機械設計においては曲げや引張と合わせて、せん断についての考慮も欠かせません。
本記事では、せん断力の意味・求め方・許容値などを分かりやすく解説します。
せん断力・せん断応力とは
「せん断力」と「せん断応力」
物体を互い違いにずらすように働く外力を「せん断荷重」と言い、このとき物体に生じる内力を「せん断力」と言います。例えばハサミは、紙にせん断力を生じさせることで、紙を切っています。
また、単位面積あたりのせん断力を「せん断応力」と言い、記号\(\tau\)で表します。
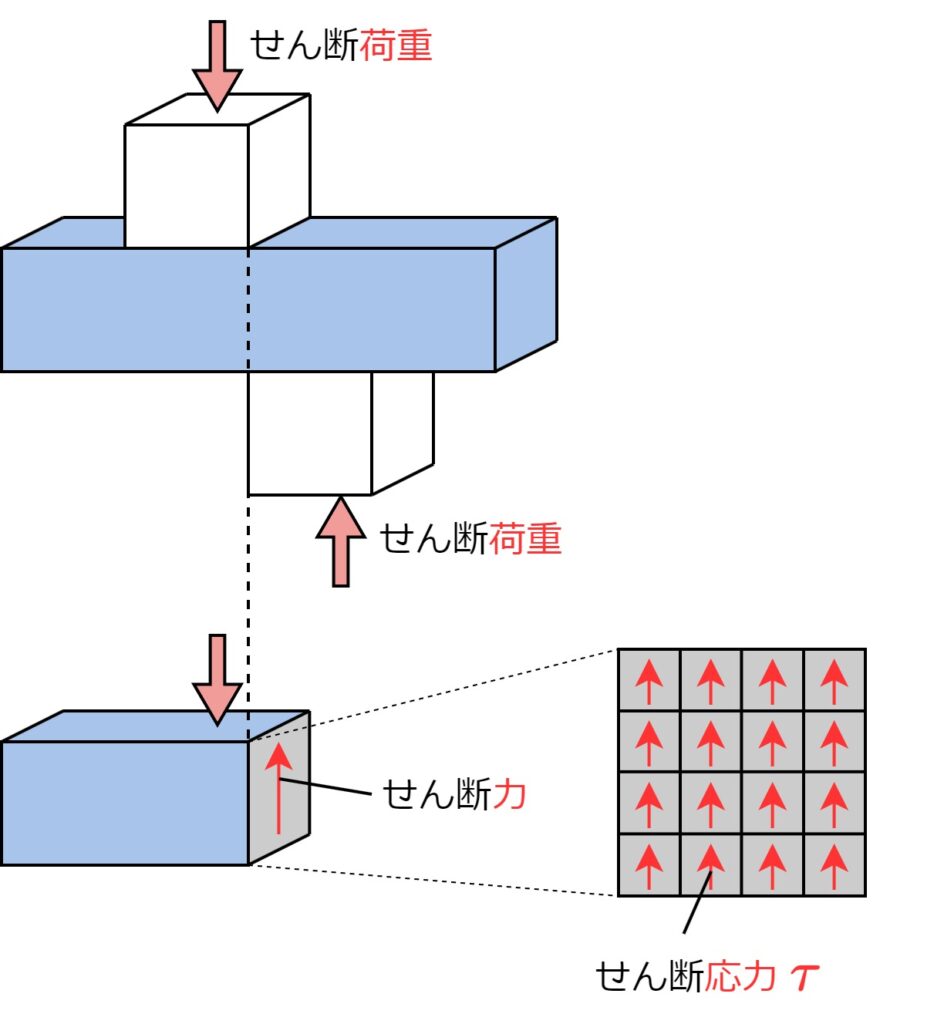
せん断力による変形：せん断ひずみ
せん断力は物体を互い違いずらす力なので、物体は下の図のように平行四辺形に変形します。
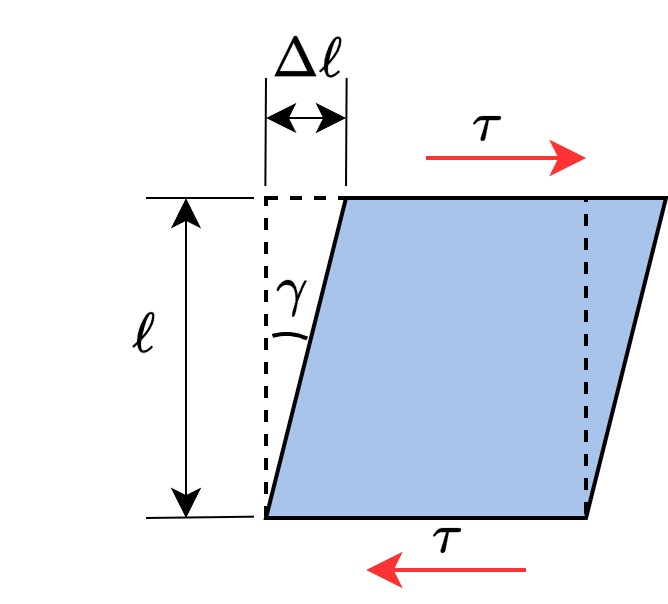
せん断ひずみ\(\gamma\)を微小としたとき、\(\gamma\)は次のように表されます。
$$\gamma=\frac{\Delta\ell}{\ell}$$
せん断弾性係数を\(G\)とすると、フックの法則より以下が成り立ちます。
$$\gamma=\frac{\tau}{G}$$
せん断応力の求め方
せん断応力は断面上で一定ではない
基本的な考え方としては、
「せん断応力」＝「せん断力」÷「断面積」です。
ただし、せん断応力は断面上で一定とはならず、断面の中心ほど大きくなるように分布しています。そこで、代表的な値として平均せん断応力\(\tau_{ave}\)と最大せん断応力\(\tau_{max}\)を用います。
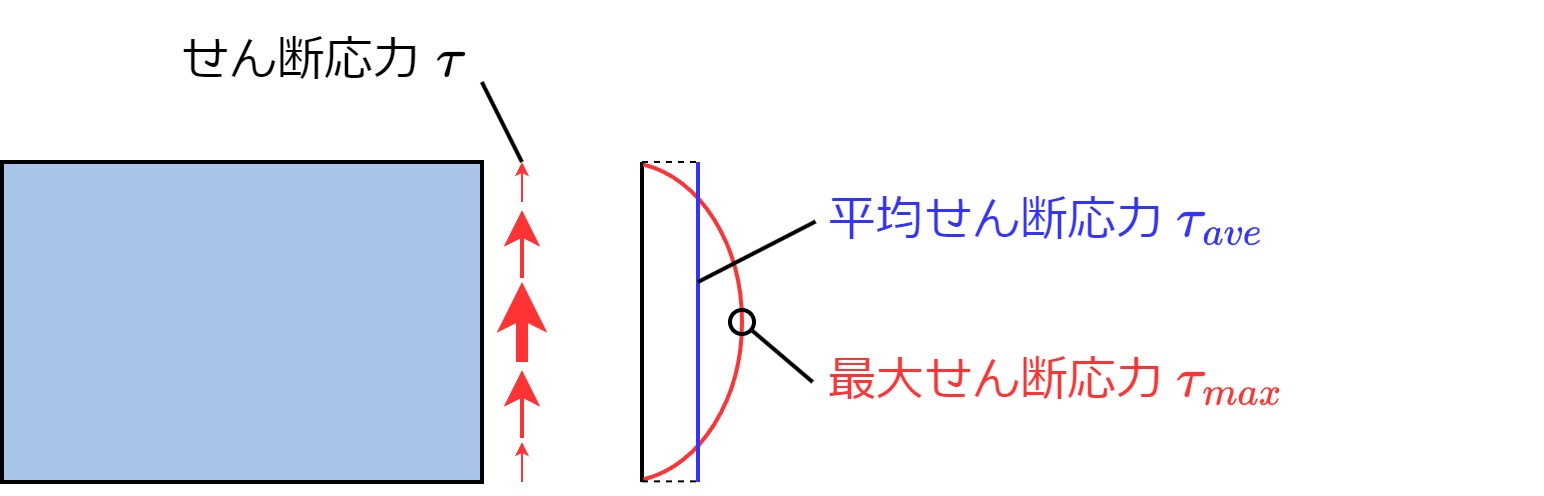
平均せん断応力の求め方
平均せん断応力は以下で求めます。
$$\tau_{ave}=\frac{F}{A}$$
- \(\tau_{ave}\)：平均せん断応力
- \(F\)：せん断力
- \(A\)：断面積
材料力学では、この平均せん断応力を単にせん断応力と呼ぶ事も多いです。
最大せん断応力の求め方
最大せん断応力は以下で求めます。
$$\tau_{max}=\frac{FS}{bI}$$
- \(\tau_{max}\)：最大せん断応力
- \(F\)：せん断力
- \(S\)：断面一次モーメント（＝面積モーメント）
- \(b\)：断面の幅
- \(I\)：断面二次モーメント
断面一次モーメント（＝面積モーメント）とは、断面の重心を求める際に使う物理量です。詳細は別記事で解説予定です（作成中）。
断面二次モーメントとは、曲げに対する変形しにくさを表す物理量で、梁のたわみを計算する際などによく使います。断面二次モーメントの詳細については別の記事で説明しています。
梁の曲げを考える際には「断面二次モーメント」が登場します。 材料力学で習いますが名前からして取っつき難く、公式は知っているが良く分からないモノ、という印象があるかと思います。 本記事では断面二次モーメントとは何か、どんな意[…]
例として、上式を使って長方形断面の最大せん断応力を求めます。
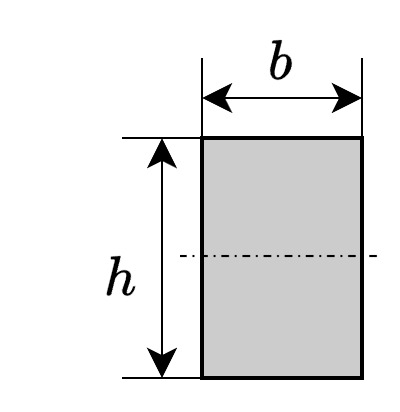
幅\(b\)、高さ\(h\)の長方形断面の場合、断面一次モーメント\(S=bh^2/8\)、断面二次モーメント\(I=bh^3/12\)ですので、最大せん断応力\(\tau_{max}\)は次のようになります。
$$\tau_{max}=\frac{FS}{bI}=\frac{F\times bh^2/8}{b\times bh^3/12}=\frac{3}{2}\times\frac{F}{bh}=1.5\times\frac{F}{A}$$
ここで、平均せん断応力\(\tau_{ave}=F/A\)ですから、
$$\tau_{max}=1.5\tau_{ave}$$
となり、長方形断面の場合、最大せん断応力\(\tau_{max}\)は平均せん断応力\(\tau_{ave}\)の1.5倍大きい事が分かります。
様々な形状と最大せん断応力
上で示した長方形断面を含め、様々な形状の最大せん断応力を示します。
梁のせん断
梁のせん断とは
荷重を受ける梁の断面には、せん断力と曲げモーメントが働きます。
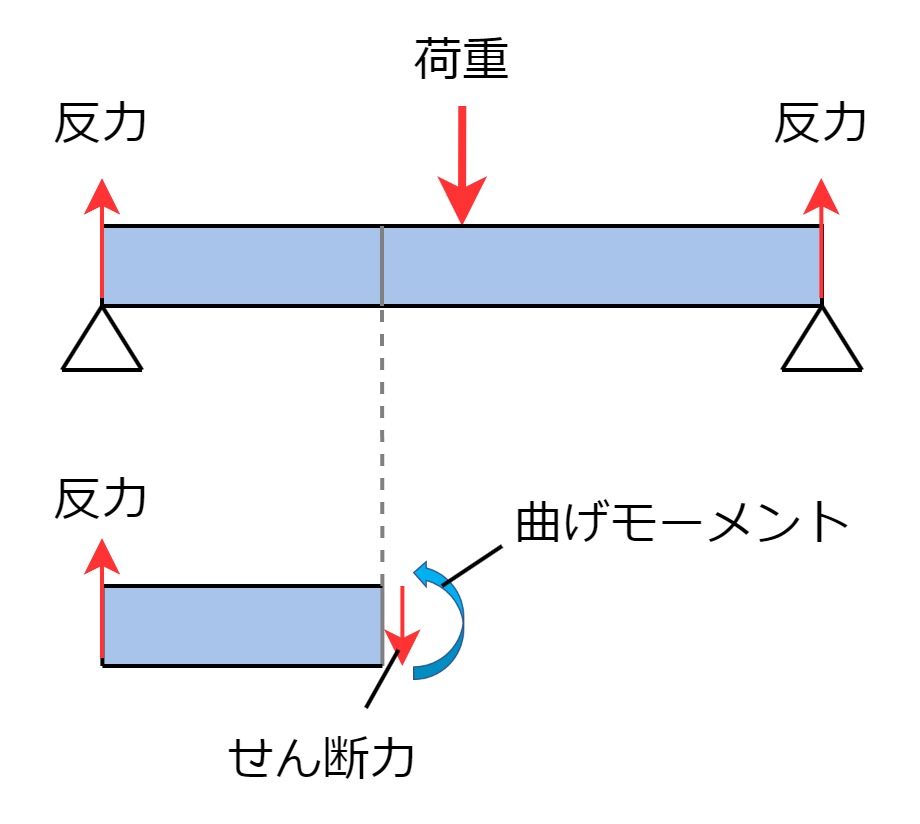
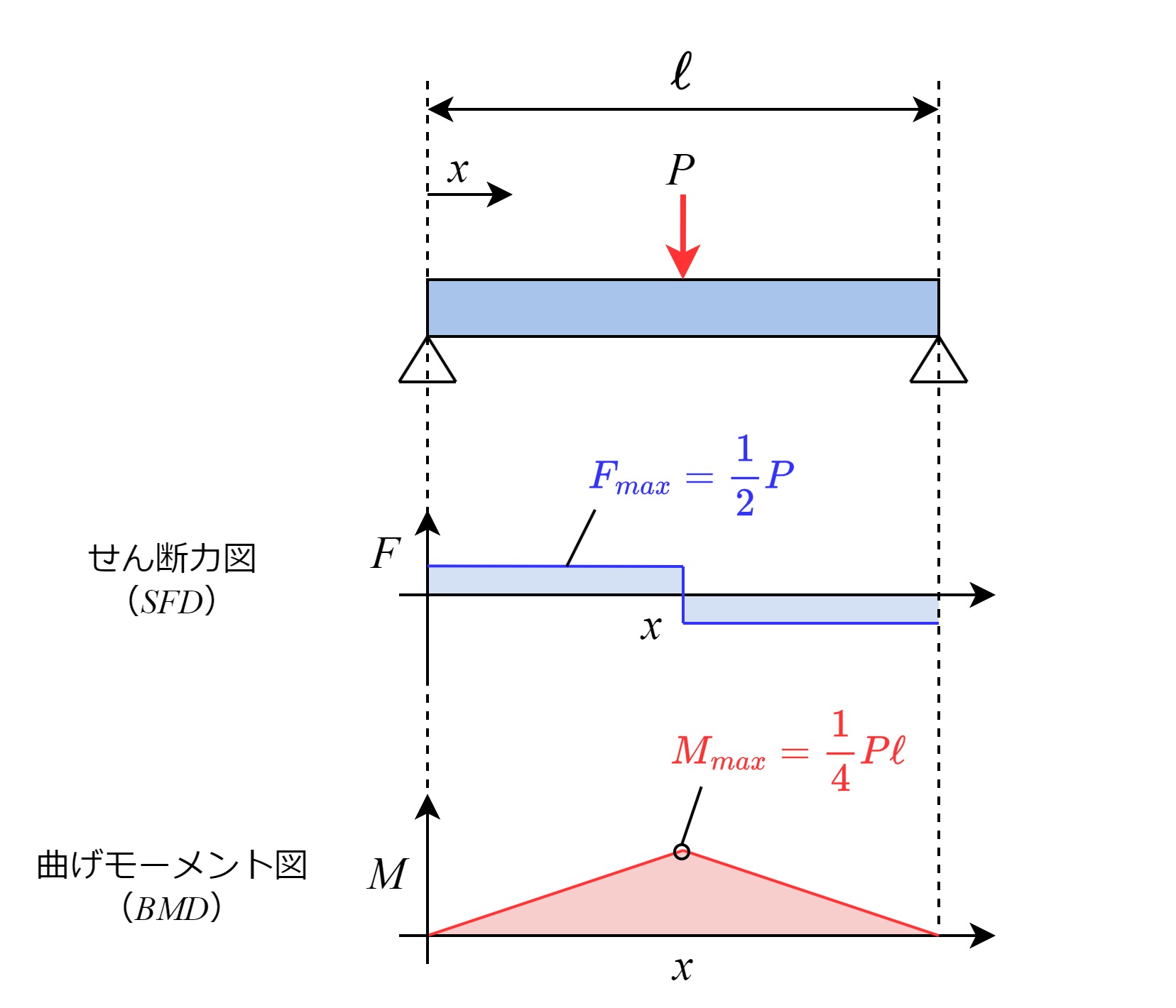
梁のせん断力・曲げモーメントは、梁を仮想的に切って断面を出現させ、力のつり合い・モーメントのつり合いを解いて求めます。上図の例の場合、せん断力\(F\)と曲げモーメント\(M\)は下図のように分布します。
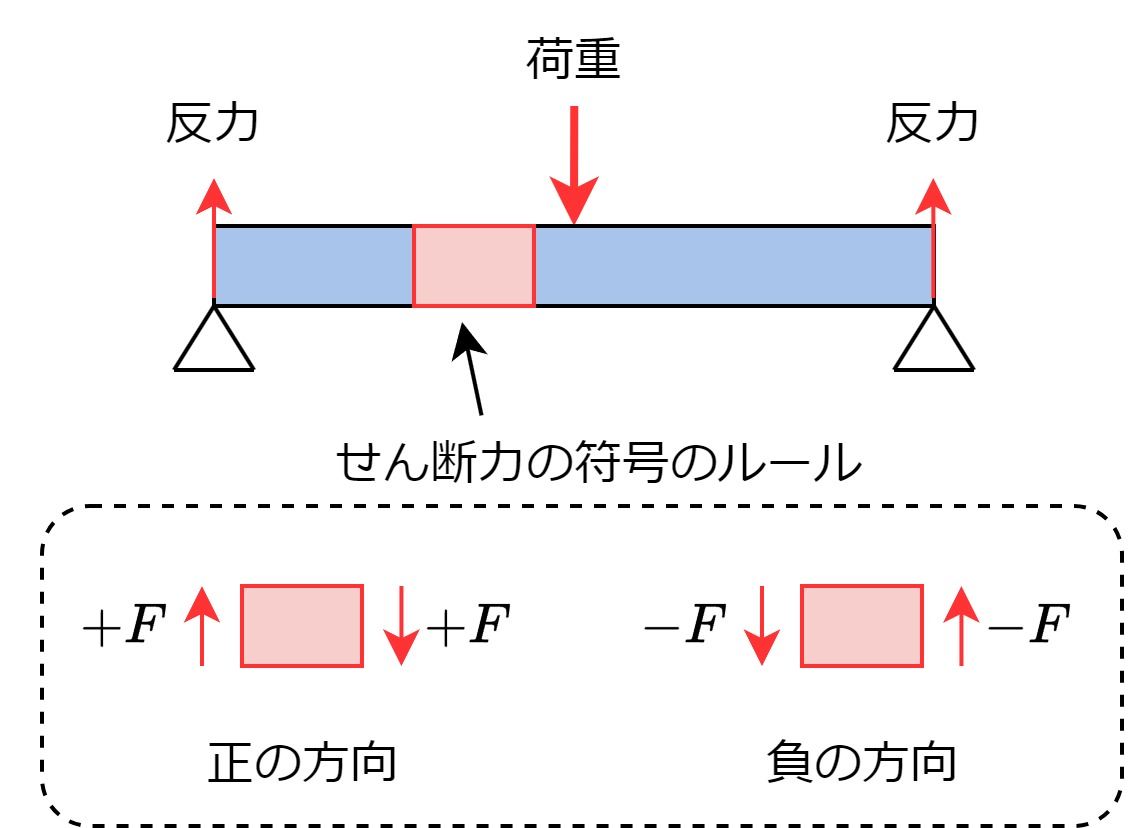
せん断力の符号が途中で変わっているのは、正負の方向にお約束があるからです（絶対値は変わりません）。梁のせん断を考える際には、下図のように正負の方向が定められているので注意しましょう。
梁のせん断力・曲げモーメントの求め方、およびせん断力図（SFD）・曲げモーメント図（BMD）の書き方については、別の記事で詳しく解説しています。
梁の曲げ問題ではせん断力と曲げモーメントを求め、その分布をグラフにした「せん断力図」と「曲げモーメント図」を作成します。 本記事では、せん断力図と曲げモーメント図の描き方と、試験等でも役立つ「覚えておくべきグラフの特徴5つ」を解説し[…]
また、曲げモーメントの計算方法・公式については、別の記事で詳しく解説しています。
梁の曲げを考える際には「曲げモーメント」が登場します。 言葉の分かりやすさから、理解した気になりやすい曲げモーメント。 本記事では、そんな曲げモーメントの考え方・計算方法・公式について一からわかりやすく解説します。 […]
梁がせん断で壊れることは、ほぼ無い
上述の通り、梁の断面にはせん断力・曲げモーメントがかかりますが、せん断力で壊れる事は稀なので、梁の曲げ問題においてはせん断応力は計算しないこともあります。
これは、曲げ応力の最大値と、せん断応力の最大値を比べた時に、曲げ応力の方がはるかに大きい事がほとんどだからです。以下に一例を示します。
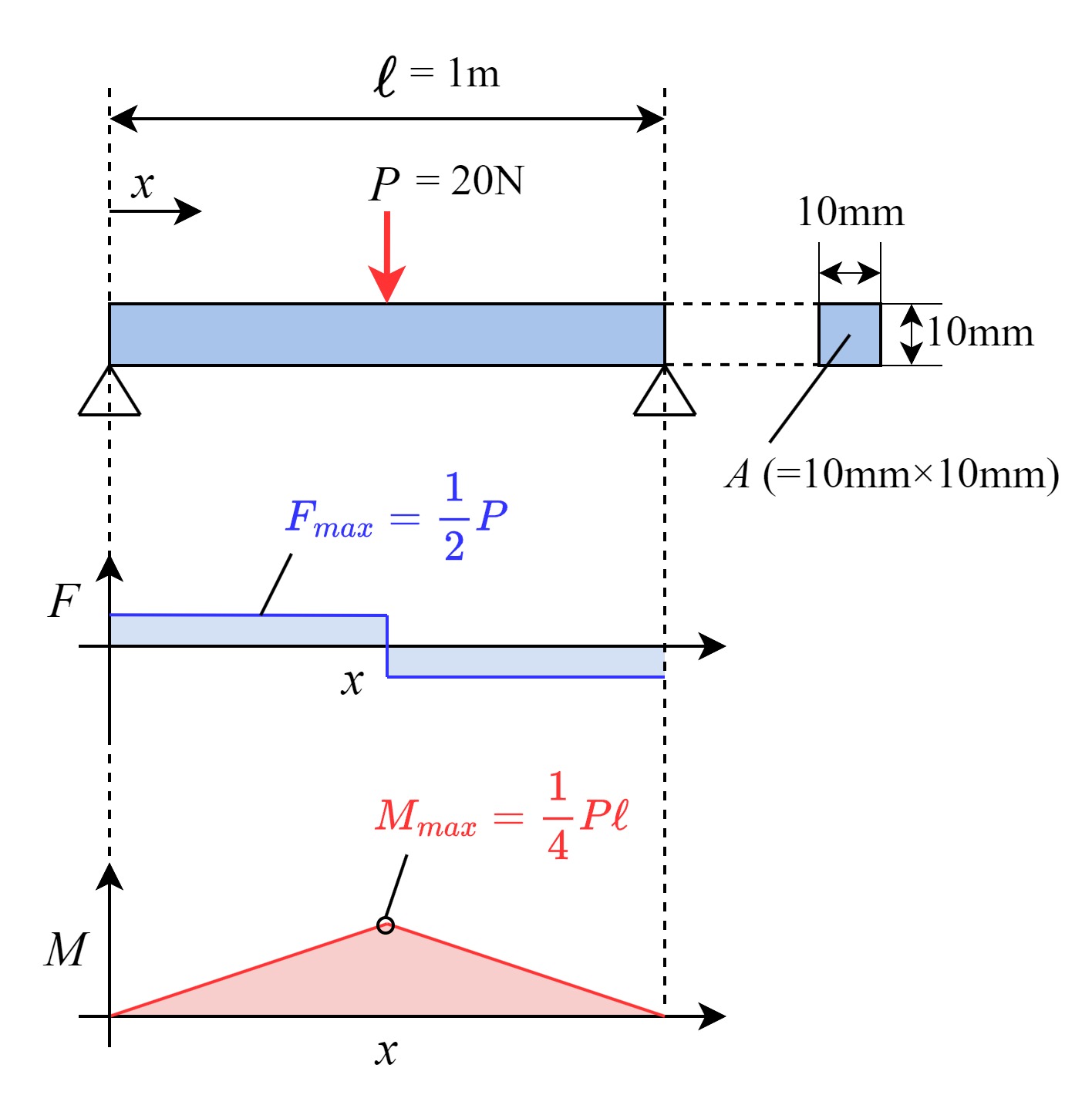
上図の梁において、平均せん断応力の最大値\(\tau_m\)と、曲げ応力の最大値\(\sigma_m\)を比較してみます。
せん断力は梁の長手方向にわたって一様なので、平均せん断応力の最大値\(\tau_m\)は次のようになります。
$$\tau_m=\frac{F_{max}}{A}=\frac{P}{2A}=0.1\ \rm{MPa}$$
一方、曲げモーメントは梁の中央で最大となります。これを断面係数\(Z\)で割れば曲げ応力ですので、曲げ応力の最大値\(\sigma_m\)は次のようになります。（断面係数\(Z\)はこちらで解説しています）
$$\sigma_m=\frac{M_{max}}{Z}=\frac{P\ell}{4\times bh^2/6}=30\ \rm{MPa}$$
よって、
平均せん断応力の最大値：\(\tau_m=0.1\ \rm{MPa}\)
曲げ応力の最大値：\(\sigma_m=30\ \rm{MPa}\)
より曲げ応力の方が300倍も大きい事が分かります。
もちろんこれは一例ですが、梁の曲げ問題では曲げ応力の方がせん断応力よりも桁違いに大きい事がほどんどなので、基本的に曲げ応力に注意して設計します。
ちなみに、せん断応力の方が大きい場合はどんな時でしょうか？
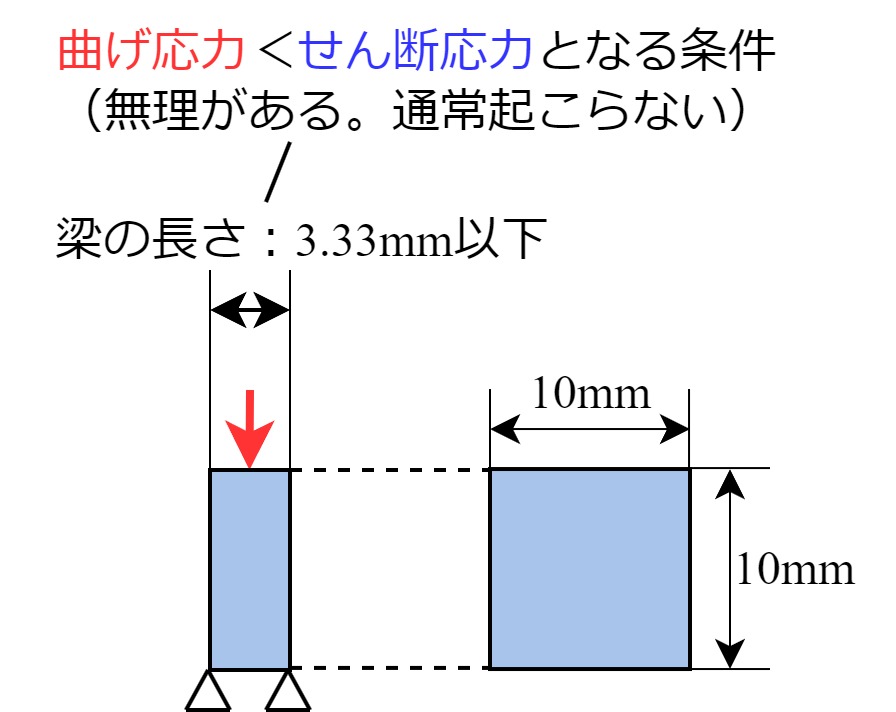
今回の例でいうと、曲げ応力が\(1/300\)以下に低減される形状に変更すれば平均せん断応力の方が大きくなります。つまり、断面形状はそのままに、\(1\ \rm{m}\)梁の長さを\(1/300\)倍する＝梁の長さを\(3.33\ \rm{mm}\)以下にするという事です。
「一辺\(10\rm{mm}\)の正方形断面に対し、梁の長さが\(3.33\rm{mm}\)以下でないと平均せん断応力の方が大きくならない」という、かなり無理のある条件だと分かります。梁はほどんどの場合、せん断応力ではなく曲げモーメンで壊れる、というイメージは湧いたかと思います。
許容せん断応力
許容せん断応力の求め方
許容せん断応力（＝せん断応力の許容値）は一般に、降伏応力\(\times 1/\sqrt{3}\)で求めます。
$$\tau_A=\frac{1}{\sqrt{3}}\sigma_Y$$
- \(\tau_A\)：許容せん断応力
- \(\sigma_Y\)：材料の降伏応力
設計においては、最大せん断応力\(\tau_{max}\)が許容せん断応力\(\tau_A\)以下となるように注意します。
$$\tau_{max}<\tau_A=\frac{1}{\sqrt{3}}\sigma_Y$$
許容せん断応力\(\tau_A\)が材料の降伏応力\(\sigma_Y\)に比例するのはイメージしやすいと思いますが、係数\(1/\sqrt{3}\)の意味については後述します。
なお、材料力学においては単純に平均せん断応力\(\tau_{ave}\)を使って
$$\tau_{ave}<\tau_A=\frac{1}{\sqrt{3}}\sigma_Y$$
とする場合も多いです。平均せん断応力はせん断力÷断面積ですぐに求まる上、前述の通り梁の曲げ問題ではせん断で壊れることはほぼありません。実用性とリスクを天秤に掛け、厳密な議論はされていないのだと思います。ただし、許容せん断応力の設定に平均せん断応力\(\tau_{ave}\)を使う場合は、安全率を十分に見た設計とするべきです。
許容せん断応力の係数は、ミーゼスの降伏条件から来る
許容せん断応力の係数\(1/\sqrt{3}\)の意味は何でしょうか？これはミーゼスの降伏条件によるものです。
材料がどんな応力状態になると破壊するか？という条件には諸説あり、その中で最も広く使われるのが「ミーゼスの降伏条件」です。ミーゼスの降伏条件とは、以下に示すミーゼス応力\(\sigma_{Mises}\)が降伏応力\(\sigma_Y\)に到達したときに、材料が破壊するという考え方です。
$$\sigma_{Mises}=\sqrt{\frac{(\sigma_1-\sigma_2)^2+(\sigma_2-\sigma_3)^2+(\sigma_3-\sigma_1)^2}{2}}$$
（\(\sigma_{1,2,3}\)：材料内の3つの主応力）
式の詳細については本記事では割愛します。
上式において平面応力状態（\(x,y\)平面にしか応力が働かない）を仮定し、\(\sigma_3=0\)とします。さらに純せん断状態と考えれば、\(\sigma_1=(-\sigma_2)=\tau\)と置けます。
これらを上式に代入すると次のようになります。
$$\sigma_{Mises}=\sqrt{\frac{(\tau+\tau)^2+(-\tau-0)^2+(0-\tau)^2}{2}}=\sqrt{3}\tau$$
\(\sigma_{Mises}=\sigma_y\)に到達する時に材料が壊れる、というのがミーゼスの降伏条件ですから、
$$\tau=\frac{1}{\sqrt{3}}\sigma_Y$$
となるせん断応力\(\tau\)で材料が壊れます。これが許容せん断応力＝降伏応力\(\times 1/\sqrt{3}\)となる理由です。
本記事では詳細を割愛しましたが、ミーゼスの降伏条件については別の記事で詳しく解説しています。
材料が降伏（破壊）するか否かを判定する基準を「降伏条件」と言います。 材料力学を習った方は「ミーゼスの降伏条件」や「トレスカの降伏条件」という単語は聞き覚えがあるかと思います。 本記事では降伏条件の考え方、グラフの意味、使[…]
まとめ
せん断力の意味・求め方・許容値について解説しました。
ポイントをまとめます。
- せん断力とは、物体を互い違いにずらすように働く内力のこと。
- せん断応力は断面上で一定ではないので、平均せん断応力\(\tau_{ave}\)と最大せん断応力\(\tau_{max}\)で議論する。
- 平均せん断応力\(\tau_{ave}\)はせん断力÷断面積で求める。
- 最大せん断応力\(\tau_{max}\)は以下で求める。
$$\tau_{max}=\frac{FS}{bI}$$
（\(F\)：せん断力、\(S\)：断面一次モーメント、\(b\)：断面の幅、\(I\)：断面二次モーメント） - 許容せん断応力は、材料の降伏応力\(\times 1/\sqrt{3}\)で求める。
皆様の参考になれば幸いです。
