配管流量を測定する機器として「ベンチュリ管」があります。
ベルヌーイの定理を応用した機器で、流体力学の授業などでよく登場します。
本記事ではベンチュリ管の測定原理を図解と共に分かりやすく説明します。
ベンチュリ管とは
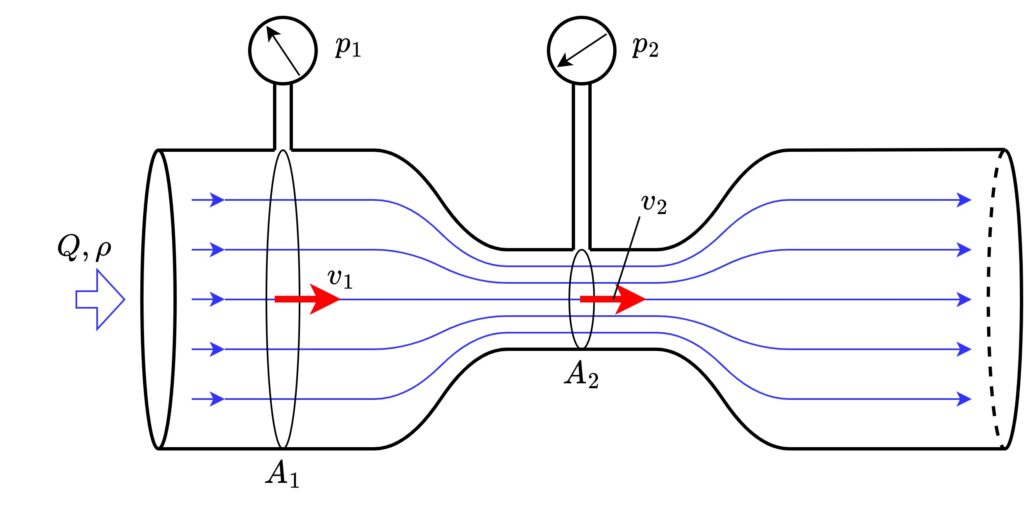
ベンチュリ管とは配管の「流量」を測定する機器で、管路の途中が絞られた構造をしています。
「絞られた箇所は流速が速くなる代わりに圧力が下がる」というベルヌーイの定理を利用し、絞る前後の圧力差から、計算により流量を求めます。
プラント設備では流量測定機器として利用されるほか、流体力学の授業においてベルヌーイの定理を理解するための題材としてもよく登場します。
ベンチュリ管の測定原理
「ベルヌーイの定理」と「連続の式」
ベンチュリ管の測定原理を説明する上で必要な「ベルヌーイの定理」と「連続の式」について説明します。
ベルヌーイの定理
ベルヌーイの定理とは「流体のエネルギー保存の法則」を示す定理で、以下の式で表されます。
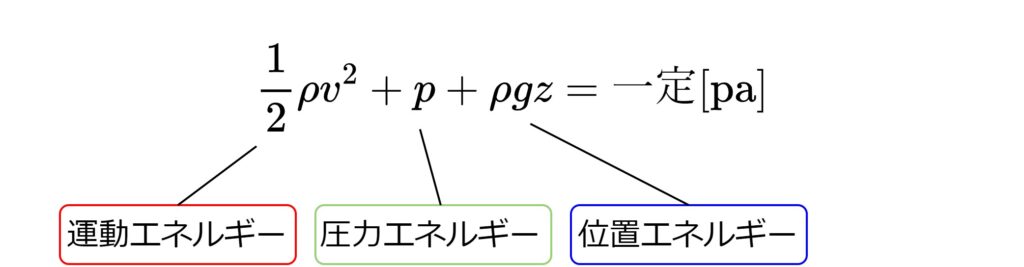
- \(\rho\):流体の密度 \(\rm{(kg/m^3)}\)
- \(v\):流速 \(\rm{(m/s)}\)
- \(p\):圧力 \(\rm{(pa)}\)
- \(g\):重力加速度 \(\rm{(m/s^2)}\)
- \(z\):高さ・水深 \(\rm{(m)}\)
運動エネルギー、圧力エネルギー、位置エネルギーは各々交換する事が可能で、その総和は一定になる、という流体力学において重要な定理です。
ただし、比較する2点が同一の流線上にある場合、などの成立条件があります。ベルヌーイの定理については別の記事で詳しく解説しています。
ボールを空中に投げた時、位置エネルギーと運動エネルギーの総和は一定となり「エネルギー保存の法則」が成り立ちます。 これを流体に当てはめたのが「ベルヌーイの定理」です。 本記事ではベルヌーイの定理・考え方を初心者にもわかりや[…]
連続の式
連続の式とは、「外部とのやりとりが無い限り、流体の質量流量はどの断面でも常に一定である」という定理です。
難しく聞こえますが簡単に言うと「流路が細い箇所ほど流速が大きくなる」という意味で、ホースで水を撒く際に先端をつぶすと流速が速くなるのと同じメカニズムです。
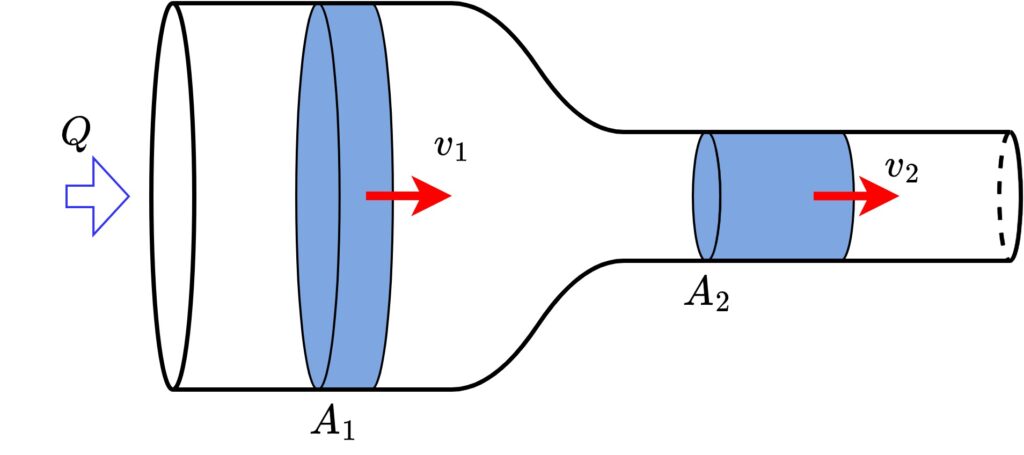
上の図のように流量\(Q\)が流れる管路において、断面積\(A_1\)の箇所の流速を\(v_1\)、断面積\(A_2\)の箇所の流速を\(v_2\)とすると、以下の式が成り立ちます。
$$Q=v_1 A_1=v_2 A_2$$
考えてみると当たり前に感じると思います。これが連続の式です。
ベンチュリ管の測定原理(図解)
上で紹介した「ベヌーイの定理」と「連続の式」を使ってベンチュリ管の測定原理を解説します。
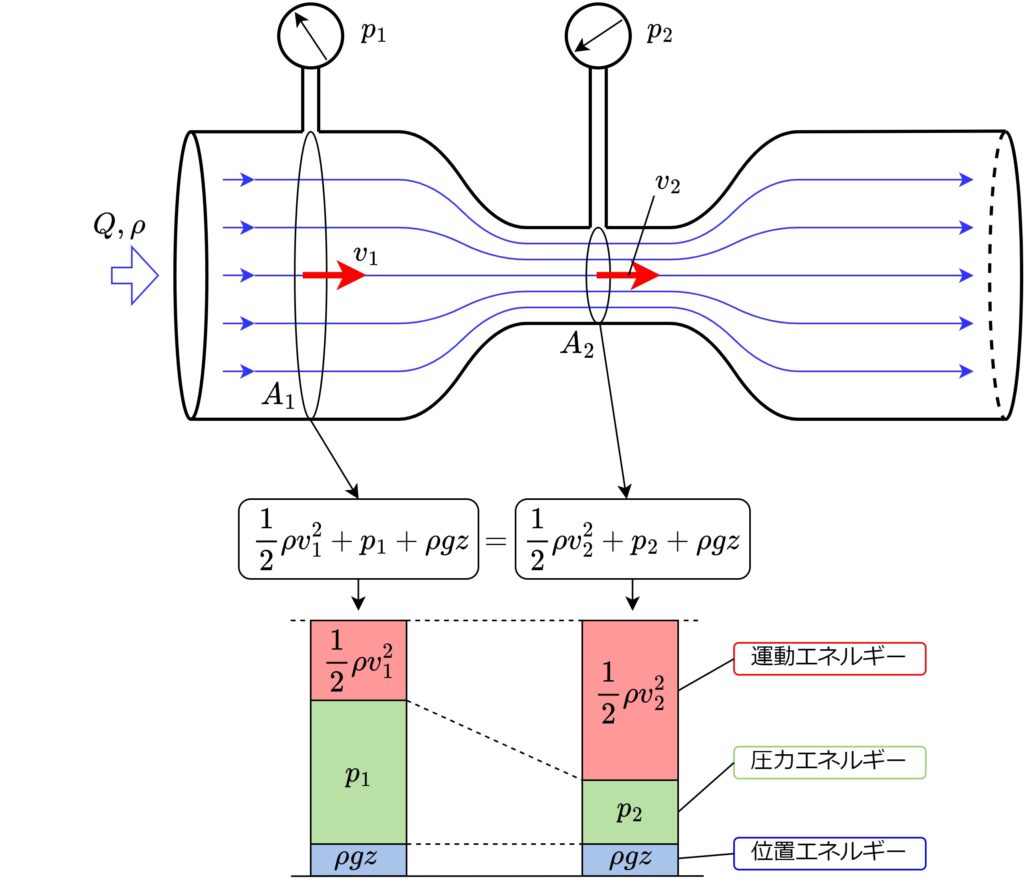
図のように流量\(Q\)、密度\(\rho\)の流体をベンチュリ管に通した時、
管路が太い箇所:断面積\(A_1\)、流速\(v_1\)、圧力\(p_1\)
管路が細い箇所:断面積\(A_2\)、流速\(v_2\)、圧力\(p_2\)
であるとすると、ベルヌーイの定理より以下の関係が成り立ちます。
$$\frac{1}{2}\rho v_1^2+p_1+\rho gz=\frac{1}{2}\rho v_2^2+p_2+\rho gz$$
管路が太い箇所・細い箇所でエネルギーの配分は異なりますが総和は同じとなります。
細い箇所は流速が速くなるため運動エネルギーが大きくなる分、圧力エネルギーが減る事でエネルギーの均衡が保たれます。またベンチュリ管は通常、水平に置きますから位置エネルギー\(\rho g z\)は左右で打ち消されます。
これを踏まえて上式を変形すると以下のようになります。
$$p_1-p_2=\frac{1}{2}\rho \left( v_2^2-v_1^2\right)$$
ここで連続の式:\(Q=v_1 A_1=v_2 A_2\)より、流速\(v_1,v_2\)を消去すると以下のようになります。
$$p_1-p_2=\frac{1}{2}\rho \left(\frac{1}{A_2^2}-\frac{1}{A_1^2}\right)Q^2$$
式変形すると、
$$Q=\sqrt{\frac{1}{\frac{1}{A_2^2}-\frac{1}{A_1^2}}} \times \sqrt{\frac{2\left(p_1-p_2\right)}{\rho}}$$
まとめると以下のようになり、絞る前後の差圧から流量\(Q\)を求める事ができます。
$$Q=\frac{A_2}{\sqrt{1-\left(A_2/A_1\right)^2}} \times \sqrt{\frac{2\left(p_1-p_2\right)}{\rho}}$$
以上がベンチュリ管の測定原理です。
なお実際には流体の粘性による圧力損失が発生するため、流量\(Q\)はこれよりも若干小さくなります。これを考慮して流量\(Q\)は流量係数\(C\)を用いて次のように補正されます。
$$Q=C\frac{A_2}{\sqrt{1-\left(A_2/A_1\right)^2}} \times \sqrt{\frac{2\left(p_1-p_2\right)}{\rho}}$$
流量係数\(C\)はベンチュリ管の型式によって異なりますが\(0.96\)~\(0.99\)程度の値となります。
差圧をマノメーターで見る場合
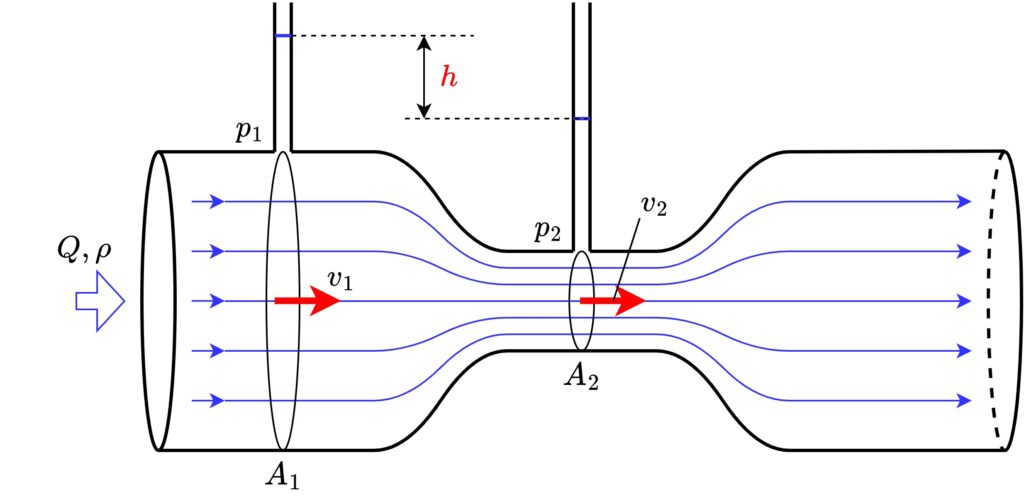
上図のように絞る前後の差圧をマノメーターで見る場合は、差圧を次のように表します。
$$p_1-p_2=\rho gh$$
従って流量\(Q\)は次のように書けます。
$$Q=\frac{A_2}{\sqrt{1-\left(A_2/A_1\right)^2}} \times \sqrt{2gh}$$
授業や資格試験などでは、こちらの書き方の方が良く見るかもしれません。
ベンチュリ管の特徴
ベンチュリ管の特徴としてメリット・デメリットを記載します。
メリット
異物に強い
絞る箇所でも管路はある程度太いので、ゴミ等の異物が詰まり難い構造となっています。
メンテナンスコストが低い
消耗部品がなくメンテナンスコストが低く抑えられます。またフランジ付き単管の構造なので取り外し・取り付けが容易です。
圧力損失が少ない
オリフィス等の流量測定機器と比較すると圧力損失が少なく済みます。
デメリット
製作の許容誤差が小さい
管径の製作精度が測定結果に効くので、許容誤差が小さくなります。
高価
製作の難易度と機器の大きさから値段が高い傾向にあります。
配管レイアウトに制限がある
ベンチュリ管自体が長い構造であること、測定精度を上げるには機器の前後に直径の5~10倍の直管が必要なことから、配管レイアウトに制限が出ます。
オリフィス流量計、フローノズル流量計といった他の流量計との違いについては、別の記事で詳しく解説しています。
流量を測定する機器の一つに「差圧式流量計」があります。 差圧式流量計にはオリフィス流量計、ベンチュリ管流量計、フローノズル流量計などの種類があり、用途によって使い分けられます。 本記事では差圧式流量計の選定材料として、それ[…]
ベンチュリ管の使用例
プラント設備などで実際に使われるベンチュリ管の例です。
流れ方向は写真の左→右となります。

よく見ると縮小する角度に比べて、拡大する角度が緩やかになっています。
これは配管の圧力損失を減らすためです。
縮小管の場合は多少の角度をつけても圧力損失は大きくなりませんが、拡大管の場合は流れの剥離が起きやすく、少しの角度でも圧力損失が大きくなります。このような理由により、絞り前後の構造が非対称となっています。
各種形状の配管の圧力損失については別の記事で詳しく解説しています。
配管の圧力損失を計算する際、曲がりやバルブ類などの複雑形状については、損失係数や相当長さ(等価管長)を使います。 本記事では損失係数・相当長さについて、考え方と計算方法を解説します。 文献から各種係数をまとめていますので、[…]
まとめ
ベルヌーイの定理を利用したベンチュリ管の測定原理を解説しました。
ポイントをまとめます。
- ベンチュリ管は管路の途中が絞られた構造の単管であり、絞る前後の差圧から「流量」を知ることができる。
- 「絞られた箇所は流速が速くなる代わりに圧力が下がる」というベルヌーイの定理を利用している。
- 流量\(Q\)は以下で計算できる:
$$Q=\frac{A_2}{\sqrt{1-\left(A_2/A_1\right)^2}} \times \sqrt{\frac{2\left(p_1-p_2\right)}{\rho}}$$
(\(A_1,A_2\):絞る前,後の断面積、\(p_1,p_2\):絞る前,後の圧力、\(\rho\):流体密度) - 「異物に強い・メンテナンスコストが低い・圧力損失が少ない」というメリットがある一方で、「製作の許容誤差が小さい・高価・配管レイアウトが制限される」というデメリットがある。
皆様の参考になれば幸いです。








